Свободные колебания систем с конечным числом степеней свободы

Будем рассматривать на основе уравнения в прямой форме без сопротивления

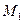
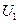
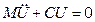(61)

Перепишем (61) в алгебраической форме (развернутой форме):

(а)

Имеем систему дифференциальных уравнений 2-го порядка, состоящую из n уравнений с постоянными коэффициентами.

Уравнения линейные:

(б)

Подставляя (б) в (а) и сокращая на 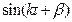дифференциальные уравнения превращаются в алгебраические и решение теперь не зависит от времени.

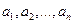- амплитуды перемещений;

k – собственная частота системы;

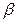- начальная фаза.

(в)

Получена система однородных алгебраических уравнений.

В этой системе неизвестными являются амплитуды 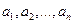и частоты k.

Для определения частоты необходимо приравнять к 0 определитель, составленный из коэффициентов перед амплитудой.

(г)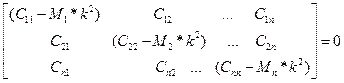

Раскрывая определитель получим уравнение n-ной степени относительно k:

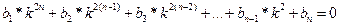(65) – вековое уравнение.

Это уравнение имеет n корней, представляющих собой собственные частоты системы.

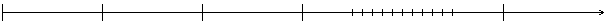k

0

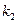
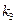
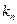
– низшая частота системы – основная частота (основной тон).

Высшие тона – оберток.

После вычисления собственных частот можно определить амплитуды колебаний.

Для решения системы (в) зададимся одной из амплитуд и разделим на неё все уравнения:

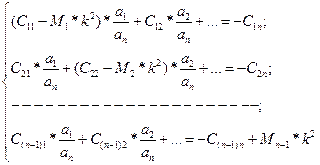
Решая эту систему уравнений, получим набор амплитуд для каждой частоты:

- набор этих амплитуд представляет собой собственную форму системы.

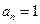
S=1

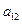
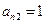
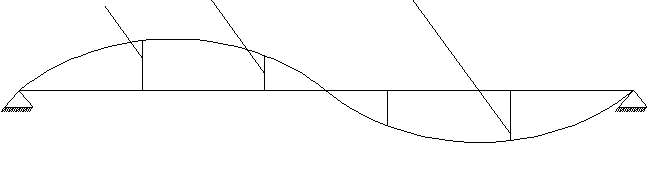S=2

Таким образом в спектре системы с конечным числом степеней свободы имеется «n» собственных частот, каждой из которых отвечает собственная форма, представляющая собой набор относительных амплитуд колебаний.

Дата добавления: 2014-01-06