Оптические явления в полупроводниках

Методические указания к курсу лекций для студентов направления 210100 – Электроника и микроэлектроника

Великий Новгород

УДК 621. 382.2 (075.8) Печатается по решению

ББК РИС НовГУ

Рецензент

доктор технических наук В.В. Гаврушко

Физика твердого тела: методические указания к курсу лекций / Сост. Б.И.Селезнёв; НовГУ им. Ярослава Мудрого. - 2 – ое изд. стереот. – Великий Новгород, 2011. – 68 с.

Методические указания составлены в соответствии с рабо­чей программой курса «Физика твердого тела», читаемого студентам направления 210100 – Электроника и микроэлектроника.

Рассмотрены оптические явления в полупроводниках, опреде­ляющие принципы действия полупроводниковых источников и прием­ников света.

УДК 621. 382.2 (075.8)

ББК

Ó Новгородский государственный

университет, 2011

Ó Селезнёв Б.И., составление, 2011

СОДЕРЖАНИЕ

Основные обозначения
1 ЭНЕРГЕТИЧЕСКИЕ СОСТОЯНИЯ В ПОЛУПРОВОДНИКАХ
1.1 Энергетическая зонная структура
1.2 Примеси в полупроводниках
1.3 Особенности легированных полупроводников
2 ОПТИЧЕСКОЕ ПОГЛОЩЕНИЕ В ПОЛУПРОВОДНИКАХ
2.1 Оптические характеристики твердых тел
2.2 Электронные переходы в полупроводниках при взаимодействии с электромагнитным излучением
2.3 Собственное поглощение
2.4 Экситонное поглощение
2.5 Влияние легирования на край собственного поглощения
2.6 Примесное поглощение
2.7 Оптическое поглощение при внутризонных переходах
2.8 Поглощение свободными носителями
2.9 Решеточное поглощение
2.10 Спектры собственного поглощения кристаллов кремния, германия и арсенида галлия
2.11 Край собственного поглощения полупроводниковых твердых растворов
3 ИЗЛУЧАТЕЛЬНАЯ РЕКОМБИНАЦИЯ В ПОЛУПРОВОДНИКАХ
3.1 Основные понятия и определения
3.2 Излучательная рекомбинация зона-зона
3.3 Излучательная рекомбинация свободных экситонов
3.4 Излучательная рекомбинация связанных экситонов
3.5 Излучательная рекомбинация примесь-зона
3.6 Межпримесная излучательная рекомбинация
3.7 Безизлучательная рекомбинация
3.8 Люминесценция полупроводников
4 ФОТОПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ
4.1 Общие представления
4.2 Фотоответ в области сильного поглощения
4.3 Примесная фотопроводимость
Список литературы

Основные обозначения:

a – постоянная решетки

a_D –боровский радиус донорного центра

a_Н –боровский радиус атома водорода

a_ex –боровский радиус экситона

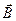– вектор магнитной индукции

с – скорость света в вакууме

D – коэффициент амбиполярной диффузии

Е_с – энергия дна зоны проводимости

Е_v – энергия потолка валентной зоны

Е_g – ширина запрещенной зоны

Е_gx – экситонная ширина запрещенной зоны

Δ Е_D,A – энергия ионизации доноров (акцепторов)

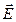– вектор напряженности электрического поля

е – абсолютная величина заряда электрона

ħ – постоянная Планка, деления на 2π

– вектор плотности тока

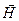– вектор напряженности магнитного поля

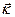– волновой вектор электрона

к – постоянная Больцмана

L – длина амбиполярной диффузии

m₀ – масса изолированного электрона

m_n,p – скалярная эффективная масса электрона (дырки)

m_r – приведенная эффективная масса

n – концентрация свободных электронов; главное квантовое число

N – концентрация примеси

N_D,A – концентрация доноров, акцепторов

N_c – эффективная плотность состояний в зоне проводимости

P – концентрация свободных дырок

p_v – эффективная плотность состояний в валентной зоне

R(ν) – скорость рекомбинации

s – скорость поверхностной рекомбинации

α – коэффициент поглощения

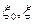– диэлектрическая проницаемость вакуума, полупроводника

λ – длина волны де Бройля

μ_n,p– дрейфовая подвижность электронов (дырок)

σ – удельная проводимость

τ_n,p– время жизни неравновесных электронов (дырок)

ψ – одноэлектронная волновая функция

ω – круговая частота электромагнитной волны

Ω – собственная частота фононов

1 ЭНЕРГЕТИЧЕСКИЕ СОСТОЯНИЯ В ПОЛУПРОВОДНИКАХ

1.1 Энергетическая зонная структура

Под энергетической зонной структурой понимается связь между энергией и импульсом носителей в твердом теле. Кинети­ческая энергия электрона связана с его квазиимпульсом клас­сическим соотношением:

(1.1)

где – эффективная масса электрона (которая может отли­чаться от массы электрона в вакууме).

Из квантовой механики известно следующее соотношение:

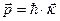(1.2)

где 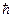– постоянная Планка;

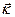– волновой вектор.

Если рассматривать кристалл в виде прямоугольной потенциаль­ной ямы с шириной L и с барьером бесконечной высоты, то оказывается, что 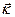может принимать дискретные значения

где n – любое целое число (кроме нуля);

L – суммарная длина;

N – элементарных ячеек раз­мером a.

Поэтому a есть наименьшая ширина потенциальной ямы, которую можно себе представить в кристалле.

Следователь­но, если , то 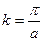есть максимальное (из фи­зически различных) значений k. Этому максимальному значе­нию соответствует край зоны Бриллюэна.

Зона Бриллюэна пред­ставляет собой объем 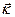– пространства, содержащий все зна­чения 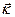вплоть до 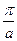, где а зависит от направления. Большим значениям 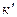отвечает просто сдвиг системы в следую­щую зону Бриллюэна, которая идентична первой зоне, поэтому можно считать, что система характеризуется волновым вектором .

Кинетическую энергию электрона можно записать в виде:

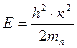(1.3)

В кристалле, имеющем форму куба с ребром L и рассмат­риваемом как потенциальная яма, разрешенные значения энергии есть

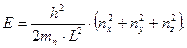(1.4)

Хотя Е принимает дискретные значения, поскольку кванто­вые числа n могут быть только целыми, то расстояния между уровнями столь малы (10^-18 эВ для кристалла объемом 1 см), что спектр E можно считать квазинепрерывным.

Зависимость энергии от волнового вектора для одного на­правления в пространстве волновых векторов является параболи­ческой, рисунок 1.1 (параболическая долина).

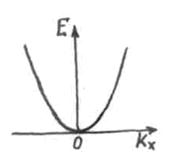
Рисунок 1.1 – Зависимость энергии от волнового вектора для одномерного случая

Рисунок 1.2 – Зависимость энергии от волнового вектора для

трехмер­ного случая

В трехмерном пространстве волновых векторов поверхности постоянной энергии представляют собой замкнутые оболочки: с увеличением волнового вектора соответствующая энергия растет квадратично (рисунок 1.2).

На рисунке 1.3 приведена зависимость энергии от волнового вектора для полупроводника с прямой структурой зон. Отрицатель­ная кривизна валентной зоны означает, что если бы электроны, находящиеся в ней, могли двигаться (т.е. если бы зона не была заполнена), то они приобретали бы ускорение в направлении, про­тивоположном тому, в каком они двигались бы, находясь в зоне проводимости. Электроны валентной зоны как бы обладают отрица­тельной массой. Для устранения представления об отрицательной эффективной массе таким электронам у потолка зоны приписывает­ся положительный заряд. Эти положительные электроны называют­ся дырками.

Расстояние между ближайшими атомами зависит от направле­ния. По этому форма поверхности постоянной энергии не должна быть в точности сферической. Более того, из-за взаимодействия с ближайшими соседями, со следующими за ними и с соседями бо­лее высокого порядка минимум долины может оказаться не в точ­ке , а в некоторой точке, находящейся на определенном кристаллографическом направлении, например (111) (рисунок 1.4).

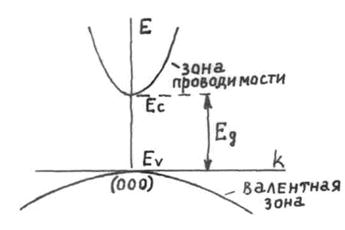
Рисунок 1.3 – Зависимость энергии от волнового вектора для системы двух зон с прямыми переходами

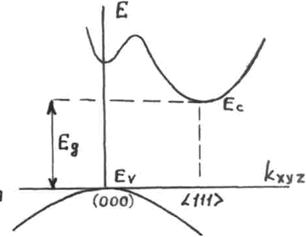
Рисунок 1.4 – Зависимость энергии от волнового вектора для полу­проводника, у которого в зоне проводимости имеются минимумы (долины) пр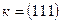и и

Из-за свойств симметрии кристалла такое же распределение должно повторяться во всех эквивалентных направ­лениях. Поэтому может быть 4 или 8 долин в направлениях и 3 или 6 долин в направлениях 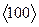. Меньшие из указанных чисел относятся к тому случаю, когда долины находятся на краю зоны Бриллюэна (при 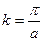, где a – постоянная решетка) и принадлежат одновременно двум зонам.

1.2 Примеси в полупроводниках

1.2.1 Мелкие водородоподобные примеси

Мелкими называются примеси, для которых расстояния от энергетического уровня залегания примеси до ближайшей к нему зоны мало по сравнению с полушириной запрещенной зоны. Такие уровни возникают, например, в германии и кремнии при введении туда примесей V и III групп периодической системы.

Рассмотрим в качестве примера атом элемента пятой груп­пы, мышьяк, введенный в Ge или Si. Пятый электрон мышья­ка, не принимая участия в образовании ковалентных связей, всту­пает в сравнительно слабое взаимодействие с большим числом атомов полупроводника. Его связь с атомом мышьяка уменьшит­ся, он начнет двигаться по орбите большого радиуса, охватываю­щей большое число атомов основного вещества. Влияние кристал­лической решетки может быть усреднено с помощью статической диэлектрической проницаемости и эффективной массы (приближение эффективной массы).

Собственные значения энергии для мелких водородоподобных примесей даются выражением:

(1.5)

где 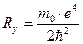– постоянная Ридберга, ;

– масса электрона в вакууме;

– главное квантовое число;

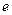– заряд электрона.

По аналогии с атомом водорода вводится понятие энергии ионизации донора:

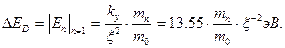(1.6)

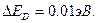Для германия . Полагая , получаем из (1.6) , что близко к экспериментальным данным для мелких доноров.

Основное состояние донора , остальные состояния -возбужденные. Таким образом, для мелкого примесного центра можно выделить основное (наинизшее) состояние и систему воз­бужденных состояний по аналогии с атомом водорода.

По аналогии с атомом водорода для примеси вводится поня­тие боровского радиуса, который характеризует орбиту электрона или объем, занимаемый электронным облаком в пространстве. Для атома водорода радиус первой боровской орбиты определяется как

(1.7)

Боровский радиус донора дается выражением:

(1.8)

Согласно (1.8) для германия 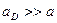, где а – постоянная решетки.

Из выражений (1.5), (1.7) и (1.8) следует, что

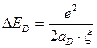(1.9)

т.е. чем больше 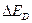, тем меньше величина боровского радиуса примесного центра .

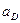1.2.2 Глубокие примесные уровни

Примеси, для которых энергия связи носителей заряда, т. е. 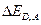, велика, образуют глубокие примесные уровни. Энер­гия ионизации для глубоких уровней (например, для уровней ме­ди и золота в германии) сравнима по порядку величины с шириной запрещенной зоны. Для описания состояний электронов, связанных с примесями, образующими глубокие локальные уровни, метод эффективной массы непригоден и нельзя пользоваться такими понятиями, как эффективная масса и диэлектрическая постоянная 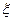, т.к. "радиус орбиты" основного состояния значительно меньше, чем для мелких примесей. Возмущающий потенциал является некулоновским и сосре­доточен в пределах центральной ячейки. Поскольку расстояния глубоких уровней от зон проводимости и валентной – одного по­рядка величины, то их нельзя считать принадлежащими одной энергетической зоне, как мелкие уровни и использовать для их описания параметры энергетической зоны (эффективную массу). В случае грубого описания глубоких уровней с помощью приближения эффективной массы, параметр должен быть заменен некото­рой комбинацией эффективных масс носителей заряда зоны прово­димости и валентной зоны, а параметр 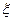должен отличаться от истинной диэлектрической постоянной кристалла.

В предельном случае глубоких примесей потенциал атомного остова апроксимируется ямой, описываемой дельта – функцией, при­чем глубина ямы подбирается такой, чтобы рассчитанная энергия связи была равна экспериментальной.

1.2.3 Примесные состояния в – пространстве

Примесную волновую функцию можно следующим образом выра­зить в виде суммы блоховских волн, относящихся к основной зоне:

(1.10)

где 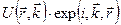– волновая функция свободного электрона в невозмущенном кристалле.

Коэффициенты 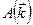опре­деляются формулой:

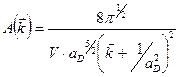(1.11)

где V – объем кристалла.

Благодаря множителю V волновая функция нормирова­на таким образом, что соответствует случаю, когда в объеме кристалла находится одно примесное состояние; величина 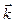отсчитывается от экстремума зоны. Из (1.11) видно, что в примесную волновую функцию существенный вклад вносят лишь значения 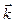вплоть до величины 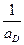. Таким образом, чем меньше радиус орбиты электрона в реаль­ном пространстве, тем сильнее примесный центр "размазан" в 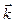– пространстве. Для глубоких неводородноподобных примесей волно­вая функция локализована в геометрическом и размазана в 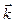– пространстве. Возбужденные состояния примесного центра сильнее локализованы в 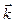– пространстве, чем основное.

1.3 Особенности легированных полупроводников

Увеличение концентрации примесей приводит к важным эф­фектам - образованию вблизи разрешенных зон хвостов плотности состояний в пределах запрещенной зоны и примесных зон.

Образование вблизи разрешенных зон хвостов плотности сос­тояний в пределах запрещенной зоны обусловлено следующими причинами. Ионизированный донор притягивает электроны зоны проводимости и отталкивает дырки валентной зоны (акцепторы действуют противоположным образом). Поскольку примеси распре­делены в кристалле хаотически, локальное взаимодействие может быть сильным или слабым в зависимости от числа примесных ато­мов, оказавшихся в данной локальной области кристалла, рисунок 1.5.

Рисунок 1.5 – Искажение краев зон за счет кулоновского взаимо­действия с неоднородно распределенными примесями (а), приводящее к образованию хвостов состояний (б)

Пунктирной кривой показана плотность состояний в отсут­ствие возмущения.

Локальная ширина запрещенной зоны – расстояние между вер­шиной валентной зоны и дном зоны проводимости – всюду остается постоянной. Но в распределении плотности состояний (представля­ющей собой число состояний при данной энергии во всем объеме кристалла) появляются участки энергии ниже дна зоны проводимос­ти и выше потолка валентной зоны.

По мере увеличения концентрации примесей, например донорных атомов, они располагаются все ближе один к другому и их волновые функции начинают все сильнее перекрываться. При этом дискретные уровни донорных электронов образуют зоны, которые расширяются с ростом уровня легирования. Представление о при­месной зоне в наиболее упрощенном виде основано на том, что распределение плотности состояний описывается гауссовой кривой, максимум которой соответствует энергетическому положению исход­ного примесного уровня. При дальнейшем увеличении концентрации примеси примесная зона может стать настолько широкой, что соль­ется с ближайшей разрешенной зоной. После такого слияния для проводимости уже не требуется, как прежде, определенной энергии активации, и температурная зависимость проводимости в таких полупроводниках носит тот же характер, что и в металлах. На рисунке 1.6 приведены зависимости энергии от расстояния между примесными центрами, выраженного в единицах .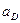

Рисунок 1.6 – Результаты расчетов, устанавливающих зависимость энергетического положения примесных уровней от расстоя­ния между атомами примесей

На нижней шкале для наглядности показаны концентрации примеси, рассчитанные при относительной диэлектрической про­ницаемости =16 и эффективной массе . Сверху указаны электронные оболочки, для которых образованные примесные зоны пересекают дно зоны проводимости 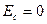. Величина определяется из выражения

(1.12)

При и Т = 10К ширина примесной зоны, образованной основным состоянием составляет примерно kT, так что при соответствующей концентрации можно считать, что примес­ная зона уже фактически образовалась.

Дата добавления: 2014-01-07