
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оптическое поглощение в полупроводниках
|
|
|
|
2.1 Оптические характеристики твердых тел
Распространение видимого и инфракрасного излучений в проводящей среде и поведение такого излучения на границе раздела двух различных сред описываются уравнениями Максвелла, характеризующими в самом общем виде распространение электромагнитных волн. Эти уравнения записываются в виде
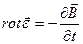 (2.1)
(2.1)
 (2.2)
(2.2)
 (2.3)
(2.3)
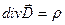 (2.4)
(2.4)
где обозначения имеют общеизвестный смысл.
Для однородной изотропной среды
 (2.5)
(2.5)
 (2.6)
(2.6)
 (2.7)
(2.7)
где  – удельная электрическая проводимость;
– удельная электрическая проводимость;
 – относительная магнитная проницаемость;
– относительная магнитная проницаемость;
 – относительная диэлектрическая проницаемость;
– относительная диэлектрическая проницаемость;
 – магнитная и диэлектрическая проницаемости вакуума.
– магнитная и диэлектрическая проницаемости вакуума.
Предполагается, что  , это справедливо для среды с достаточно высокой проводимостью.
, это справедливо для среды с достаточно высокой проводимостью.
С учетом (2.5 – 2.7) уравнения (2.1 – 2.4) имеют вид:
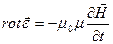 (2.8)
(2.8)
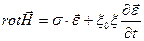 (2.9)
(2.9)
 (2.10)
(2.10)
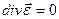 (2.11)
(2.11)
Из (2.9) и (2.10), учитывая, что 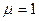 для всех рассматриваемых материалов в оптическом диапазоне следует уравнение
для всех рассматриваемых материалов в оптическом диапазоне следует уравнение
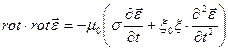 (2.12)
(2.12)
или при упрощении
 (2.13)
(2.13)
Аналогичное уравнение получается для вектора 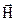 .
.
Решение для одного из компонентов вектора  имеет вид:
имеет вид:
 (2.14)
(2.14)
где  – комплексный показатель преломления;
– комплексный показатель преломления;
 – круговая частота;
– круговая частота;
 – скорость распространения света в вакууме.
– скорость распространения света в вакууме.
Это решение удовлетворяет уравнению (2.13) при условии
 (2.15)
(2.15)
Выражение (2.14) описывает волну, распространяющуюся в направлении  с постоянной распространения
с постоянной распространения  , которая, в общем случае, является комплексной величиной. Если проводимость среды равна нулю, то величина
, которая, в общем случае, является комплексной величиной. Если проводимость среды равна нулю, то величина  вещественна и отношение
вещественна и отношение  равно скорости распространения волны, так что
равно скорости распространения волны, так что  отождествляется с величиной
отождествляется с величиной  – показателем преломления среды.
– показателем преломления среды.
Если же среда характеризуется конечной проводимостью, то можно ввести комплексный показатель преломления, который запишется в виде
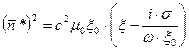 (2.16)
(2.16)
Для вакуума, когда  ,
,  и
и  , получаем известное соотношение
, получаем известное соотношение  и, следовательно,
и, следовательно,
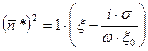 (2.17)
(2.17)
Если представить комплексную величину  в виде вещественной и мнимой частей
в виде вещественной и мнимой частей
 (2.18)
(2.18)
то уравнение (2.14) запишется следующим образом:
 (2.19)
(2.19)
Это выражение описывает волну с частотой  , распространяющуюся со скоростью
, распространяющуюся со скоростью 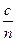 и затухающую по экспоненте, в показателе которой стоит число k, характеризующее поглощение в среде.
и затухающую по экспоненте, в показателе которой стоит число k, характеризующее поглощение в среде.
Мнимая часть комплексного показателя преломления к, называется показателем поглощения (показателем затухания) или коэффициентом экстинкции.
Аналогичное выражение для магнитного поля можно получить подстановкой найденного решения в уравнение (2.8) при 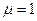 :
:
 (2.20)
(2.20)
Коэффициент поглощения  данной среды определяется условием, что энергия волны уменьшается в e раз на расстоянии
данной среды определяется условием, что энергия волны уменьшается в e раз на расстоянии 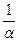 . Поток энергии пропорционален произведению амплитуд электрического и магнитного векторов. Поскольку обе эти амплитуды содержат
. Поток энергии пропорционален произведению амплитуд электрического и магнитного векторов. Поскольку обе эти амплитуды содержат  , энергия волны уменьшается с расстоянием, как
, энергия волны уменьшается с расстоянием, как  и коэффициент поглощения есть
и коэффициент поглощения есть
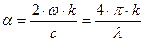 (2.21)
(2.21)
где 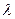 – длина волны в вакууме.
– длина волны в вакууме.
Из соотношений (2.17) и (2.18) вытекает
 (2.22)
(2.22)
 (2.23)
(2.23)
Отсюда получаем
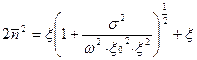 (2.24)
(2.24)
 (2.25)
(2.25)
Если 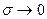 , то
, то  и
и  . Последнее соотношение выполняется в случае, когда измерения
. Последнее соотношение выполняется в случае, когда измерения 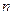 и
и  проведены либо при одной и той же частоте, либо при различных частотах, но таких, что между ними нет полос поглощения.
проведены либо при одной и той же частоте, либо при различных частотах, но таких, что между ними нет полос поглощения.
В случае нормального падения коэффициент отражения определяется формулой
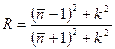 (2.26)
(2.26)
Когда 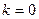 , т.е. материал прозрачен
, т.е. материал прозрачен
 (2.27)
(2.27)
Если 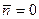 , то
, то 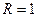 и полупроводник полностью отражает излучение.
и полупроводник полностью отражает излучение.
Коэффициент пропускания I есть отношение интенсивности света, прошедшего через образец, к интенсивности падающего, т.е. 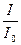 . Для плоскопараллельной пластины толщиной d выражение для коэффициента пропускания имеет вид
. Для плоскопараллельной пластины толщиной d выражение для коэффициента пропускания имеет вид
 (2.28)
(2.28)
2.2 Электронные переходы в полупроводниках при взаимодействии с электромагнитным излучением
Вероятность перехода квантовой системы из состояния а в состояние b под действием возмущения, периодически изменяющегося во времени с частотой  , равна
, равна
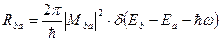 (2.29)
(2.29)
где матричный элемент перехода 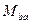 можно представить в виде
можно представить в виде
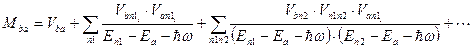 (2.30)
(2.30)
Здесь 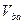 ,
,  ,
, 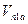 и т.д. – матричные элементы возмущения между соответствующими состояниями.
и т.д. – матричные элементы возмущения между соответствующими состояниями.
 (2.31)
(2.31)

Состояния 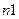 ,
,  , и т.д. являются промежуточными, виртуальными. Первое слагаемое в (2.30) учитывает непосредственные переходы из состояния а в состояние b под действием возмущения
, и т.д. являются промежуточными, виртуальными. Первое слагаемое в (2.30) учитывает непосредственные переходы из состояния а в состояние b под действием возмущения  , второе - переходы из состояния через промежуточное состояние
, второе - переходы из состояния через промежуточное состояние 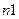 в состояние
в состояние 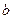 , третье -переход из a в b через два последовательных промежуточных состояния
, третье -переход из a в b через два последовательных промежуточных состояния 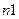 и
и  и т.д. Суммирование в (2.30) идет по всем промежуточным состояниям.
и т.д. Суммирование в (2.30) идет по всем промежуточным состояниям.
Выражение (2.30) имеет простую структуру и его удобно представить графиком типа диаграмм Фейнмана, изображающим в наглядной форме развитие процесса во времени. С каждым членом в (2.30) сопоставим диаграммы
 (2.32)
(2.32)
 (2.33)
(2.33)

 (2.34)
(2.34)
Здесь каждой точке на графике соответствует матричный элемент, например  , каждому участку между точками, например
, каждому участку между точками, например 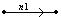 соответствует множитель вида
соответствует множитель вида
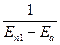 ,
,
где 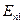 – энергия промежуточного состояния;
– энергия промежуточного состояния;
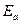 – начальная энергия.
– начальная энергия.
И наконец, по всем промежуточным состояниям проводится суммирование.
Пользуясь вполне определенными правилами можно по диаграмме написать аналитические выражения, соответствующие данному переходу. В отличие от (2.29) и (2.30) в выражениях (2.33) и (2.34) энергия фотона  для общности включена в энергию начального (для случая поглощения) или конечного (для случая испускания) состояния.
для общности включена в энергию начального (для случая поглощения) или конечного (для случая испускания) состояния.
Для того чтобы был возможен оптический переход из состояния 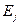 в состояние
в состояние 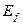 необходимо выполнить ряд условий, называемых правилами отбора. В полупроводниках эти правила отбора сводятся к выполнению законов сохранения энергии и волнового вектора.
необходимо выполнить ряд условий, называемых правилами отбора. В полупроводниках эти правила отбора сводятся к выполнению законов сохранения энергии и волнового вектора.

Рисунок 2.1 – Прямой переход из состояния j валентной зоны в состояние f зоны проводимости при поглощении фотона 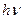 : а) изображение на диаграмме
: а) изображение на диаграмме  ; б) диаграмма взаимодействия
; б) диаграмма взаимодействия
Рассмотрим для определенности квантовый переход из состояния j валентной зоны в состояние f зоны проводимости при поглощении кванта электромагнитной энергии 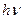 . На зонной диаграмме
. На зонной диаграмме  этот переход изображен на рисунке 2.1,а. Графическое представление этого же перехода, показывающее развитие процесса во времени, изображено на рисунке 2.1,б.
этот переход изображен на рисунке 2.1,а. Графическое представление этого же перехода, показывающее развитие процесса во времени, изображено на рисунке 2.1,б.
На языке электронно-дырочного формализма рисунке 2.1,б свидетельствует о том, что в начальном состоянии имелся фотон 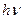 , в конечном – электрон в состоянии
, в конечном – электрон в состоянии  и дырка в состоянии
и дырка в состоянии  .
.
Точка на диаграмме означает взаимодействие и ей соответствует матричный элемент возмущения:
 (2.35)
(2.35)
где  ,
, 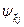 – волновые функции частиц в состояниях f и j;
– волновые функции частиц в состояниях f и j;
V – возмущение.
Интегрирование в выражении (2.35) проводится по всему объему, а значок  означает комплексное сопряжение.
означает комплексное сопряжение.
Представленные на рисунке 2.1 диаграммы изображают процессы собственного поглощения за счет переходов 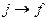 .
.
Рассмотрим условие, при котором возможен переход из состояния j в состояние f непосредственно, т.е. при взаимодействии только с фотоном. Возмущение V при этом можно записать в виде плоской монохроматической волны.
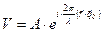 (2.36)
(2.36)
где 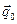 – единичный вектор в направлении движения фотона;
– единичный вектор в направлении движения фотона;
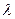 – длина электромагнитной волны в веществе.
– длина электромагнитной волны в веществе.
Волновые функции электронов в кристалле представляются в виде Блоховских функций:
 (2.37)
(2.37)
 (2.38)
(2.38)
где 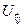 и
и 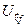 – периодические функции с периодом решетки;
– периодические функции с периодом решетки;
 и
и 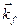 – волновые векторы.
– волновые векторы.
После подстановки выражений (2.36), (2.37) и (2.38) в выражение (2.35) подынтегральная функция в матричном элементе содержит множитель

который быстро и периодически осциллирует в пространстве, за исключением случая
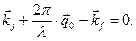 (2.39)
(2.39)
Поэтому при интегрировании по  при всех значениях
при всех значениях  и
и 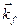 , не удовлетворяющих этому равенству, величина
, не удовлетворяющих этому равенству, величина 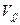 обращается в 0.
обращается в 0.
Отсюда вытекает правило отбора по волновому вектору при непосредственных оптических переходах:
 (2.40)
(2.40)
где  – волновой вектор фотона:
– волновой вектор фотона:
Условие (2.40) аналогично закону сохранения импульса. Домножив обе части выражения (2.40) на 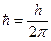 , получим правило отбора квазиимпульса:
, получим правило отбора квазиимпульса:
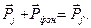 (2.41)
(2.41)
В видимой и инфракрасной областях спектра величина волнового вектора фотона  значительно меньше величины волнового вектора электрона. Поэтому величиной
значительно меньше величины волнового вектора электрона. Поэтому величиной  в выражении (2.40) можно пренебречь. Тогда в соответствии с законом сохранения при взаимодействии только с фотоном могут осуществляться только переходы без изменения волнового вектора:
в выражении (2.40) можно пренебречь. Тогда в соответствии с законом сохранения при взаимодействии только с фотоном могут осуществляться только переходы без изменения волнового вектора:
 (2.42)
(2.42)
Именно поэтому на диаграмме (2.1,а) соответствующий переход изображен вертикальной линией и называется прямым или вертикальным переходом. Для реального перехода должен также выполняться закон сохранения энергии.
Таким образом, непосредственные оптические переходы возможны только между состояниями с одинаковыми волновыми векторами, т.е. расположенными в одной и той же точке  – пространства. Во многих полупроводниках (Ge, Si, GaP,…..SiC …и др.) абсолютный минимум зоны проводимости и максимум валентной зоны расположены в различных точках зоны Бриллюэна. Поэтому непосредственные переходы между такими состояниями запрещены в первом приближении теории возмущений. Для их осуществления необходимо рассеяние квазиимпульса, которое может происходить на любых дефектах решетки – фононах, примесях, свободных носителях заряда. Тогда оптический переход между состояниями j и f, расположенными в различных точках
– пространства. Во многих полупроводниках (Ge, Si, GaP,…..SiC …и др.) абсолютный минимум зоны проводимости и максимум валентной зоны расположены в различных точках зоны Бриллюэна. Поэтому непосредственные переходы между такими состояниями запрещены в первом приближении теории возмущений. Для их осуществления необходимо рассеяние квазиимпульса, которое может происходить на любых дефектах решетки – фононах, примесях, свободных носителях заряда. Тогда оптический переход между состояниями j и f, расположенными в различных точках  – пространства, можно рассматривать следующим образом (рисунок 2.2).
– пространства, можно рассматривать следующим образом (рисунок 2.2).

Рисунок 2.2 – Непрямой оптический переход из состояния j валентной зоны в состояние f зоны проводимости при поглощении фотона 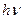 и фонона
и фонона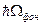 : а) изображение на диаграмме
: а) изображение на диаграмме  ; б) диаграмма взаимодействия
; б) диаграмма взаимодействия
Под действием электромагнитного возмущения электрон переходит из состояния j в промежуточное, виртуальное состояние l. Таким состоянием, например, может являться более глубоко лежащее состояние зоны проводимости. Время пребывания электрона  в этом промежуточном состоянии мало. Из соотношения неопределенности Гейзенберга
в этом промежуточном состоянии мало. Из соотношения неопределенности Гейзенберга  , следует, что неопределенность в энергии
, следует, что неопределенность в энергии 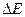 может быть достаточно велика, так что при переходе в виртуальное состояние
может быть достаточно велика, так что при переходе в виртуальное состояние 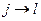 закон сохранения энергии не соблюдается. Находясь в виртуальном состоянии l малое время
закон сохранения энергии не соблюдается. Находясь в виртуальном состоянии l малое время  , электрон успевает провзаимодействовать с "третьей" частицей, например, с фононом, как это изображено на рисунке 2.2, в результате чего переходит в конечное состояние f. Полный переход
, электрон успевает провзаимодействовать с "третьей" частицей, например, с фононом, как это изображено на рисунке 2.2, в результате чего переходит в конечное состояние f. Полный переход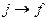 возможен, если соблюдаются законы сохранения энергии и волнового вектора. Учитывая, что фонон обладает энергией
возможен, если соблюдаются законы сохранения энергии и волнового вектора. Учитывая, что фонон обладает энергией 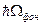 и волновым вектором
и волновым вектором  , соответствующие законы сохранения при оптических переходах с участием фононов имеют вид:
, соответствующие законы сохранения при оптических переходах с участием фононов имеют вид:
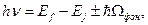 (2.43)
(2.43)
 (2.44)
(2.44)
Знаки (+) и (-) в выражениях (2.43) и (2.44) соответствуют случаям поглощения и испускания фононов.
Оптические переходы между состояниями с различными значениями волного вектора называются непрямыми переходами. Они разрешены лишь во втором приближении теории возмущений с участием рассеивающих центров, и поэтому вероятность таких переходов существенно меньше, чем прямых.
2.3 Собственное поглощение
2.3.1 Прямые переходы
Рассмотрим поглощение, связанное с переходами между двумя прямыми долинами при условии, что все переходы с сохранением импульса разрешены (рисунок 2.1), т.е. вероятность перехода  не зависит от энергии фотона.
не зависит от энергии фотона.
Коэффициент поглощения  фотона с данной энергией
фотона с данной энергией  пропорционален вероятности
пропорционален вероятности  перехода из начального в конечное состояние и плотности состояний в разрешенных зонах, разделенных энергией
перехода из начального в конечное состояние и плотности состояний в разрешенных зонах, разделенных энергией  при одном и том же значении
при одном и том же значении  , так называемой комбинированной плотности состояний:
, так называемой комбинированной плотности состояний:
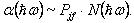
Для разрешенных прямых переходов  величина постоянная и спектральная зависимость
величина постоянная и спектральная зависимость  определяется
определяется 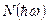 .
.
Каждому начальному состоянию 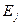 отвечает конечное состояние
отвечает конечное состояние 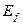 , такое что
, такое что
 (2.45)
(2.45)
Энергии 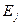 и
и 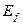 отсчитываются от краев разрешенных зон. В случае параболических зон
отсчитываются от краев разрешенных зон. В случае параболических зон
 ;
;  (2.46)
(2.46)
Поэтому
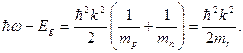 (2.47)
(2.47)
где  называется приведенной эффективной массой
называется приведенной эффективной массой

Комбинированная плотность состояний вычисляется как
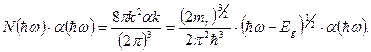 (2.48)
(2.48)
Следовательно, коэффициент поглощения выражается формулой
 (2.49)
(2.49)
где коэффициент А имеет вид
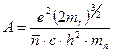 . (2.50)
. (2.50)
Принимая показатель преломления  и считая эффективные массы электрона и дырки равными массе свободного электрона, получаем:
и считая эффективные массы электрона и дырки равными массе свободного электрона, получаем:
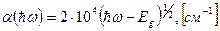
где  и
и  выражены в электронвольтах.
выражены в электронвольтах.
В некоторых полупроводниках прямые переходы при  согласно квантовым правилам отбора запрещены, а при
согласно квантовым правилам отбора запрещены, а при 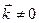 вероятность перехода увеличивается пропорционально
вероятность перехода увеличивается пропорционально  . Для структуры зон, изображенной на рисунке 3.1, это означает, что вероятность перехода увеличивается пропорционально
. Для структуры зон, изображенной на рисунке 3.1, это означает, что вероятность перехода увеличивается пропорционально 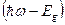 . Поскольку комбинированная плотность состояний пропорциональна
. Поскольку комбинированная плотность состояний пропорциональна 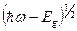 коэффициент поглощения для прямых запрещенных переходов имеет следующую спектральную зависимость:
коэффициент поглощения для прямых запрещенных переходов имеет следующую спектральную зависимость:
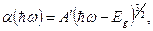 (2.51)
(2.51)
где  определяется выражением:
определяется выражением:
 .
.
Принимая  и
и  ,
,

2.3.2 Непрямые переходы
Для непрямых переходов:
 (2.52)
(2.52)
где 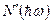 – комбинированная плотность состояний для непрямых переходов.
– комбинированная плотность состояний для непрямых переходов.
В случае непрямых переходов возможны переходы из любого занятого состояния валентной зоны в любое свободное состояние зоны проводимости.
Можно показать, что
 (2.53)
(2.53)
где  – плотность состояний в зоне проводимости;
– плотность состояний в зоне проводимости;
 – плотность со стояний в валентной зоне;
– плотность со стояний в валентной зоне;
l – число минимумов в зоне проводимости.
Энергия электрона 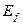 отсчитывается от дна зоны проводимости, энергия дырки
отсчитывается от дна зоны проводимости, энергия дырки 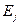 от потолка валентной зоны.
от потолка валентной зоны.
При поглощении фононов
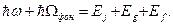 (2.54)
(2.54)
При  выражение (2.54) имеет вид
выражение (2.54) имеет вид

Тогда комбинированная плотность состояний 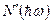 определяется выражением
определяется выражением
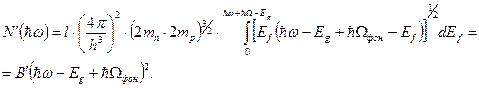 (2.55)
(2.55)
Для непрямых переходов с испусканием фононов
 (2.56)
(2.56)
Коэффициент поглощения  пропорционален вероятности взаимодействия с фононом, которая сама есть функция числа фононов
пропорционален вероятности взаимодействия с фононом, которая сама есть функция числа фононов 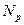 с энергией
с энергией 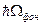 .
.
Согласно статистике Бозе-Эйнштейна, число фононов определяется формулой
 (2.57)
(2.57)
Тогда величина коэффициента поглощения для непрямых переходов с поглощением фононов определяется выражением
 (2.58)
(2.58)
где В – постоянная величина.
Вероятность испускания фонона пропорциональна 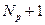 , следовательно, коэффициент поглощения для переходов с эмиссией фононов есть
, следовательно, коэффициент поглощения для переходов с эмиссией фононов есть
 (2.59)
(2.59)
Поскольку при  возможны процессы как с испусканием, так и с поглощением фононов, коэффициент поглощения представляется в виде суммы
возможны процессы как с испусканием, так и с поглощением фононов, коэффициент поглощения представляется в виде суммы 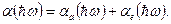
Спектральная зависимость коэффициента поглощения для непрямых межзонных переходов с участием одного типа фононов представлена на рисунке 2.3.
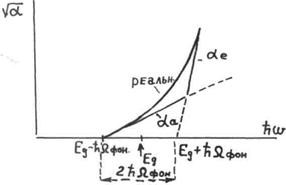
Рисунок 2.3 – Спектральная зависимость коэффициента поглощения для непрямых переходов
Для разделения процессов с испусканием и поглощением фононов необходимо исследование температурных зависимостей коэффициента поглощения. При очень низких температурах плотность фононов весьма мала (знаменатель в формуле (2.58) велик), поэтому коэффициент  также мал, т.е. при низких температурах отсутствуют процессы, идущие с поглощением фононов. Поэтому для низких температур характерны процессы с эмиссией фононов. С повышением температуры начинают проявляться процессы с поглощением фононов (рисунок 2.4). Из зависимости
также мал, т.е. при низких температурах отсутствуют процессы, идущие с поглощением фононов. Поэтому для низких температур характерны процессы с эмиссией фононов. С повышением температуры начинают проявляться процессы с поглощением фононов (рисунок 2.4). Из зависимости 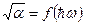 определяются ширина запрещенной зоны и энергии фононов.
определяются ширина запрещенной зоны и энергии фононов.
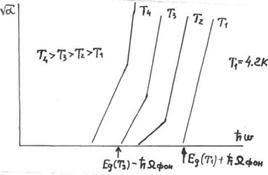
Рисунок 2.4 – Температурные зависимости коэффициента поглощения для непрямых переходов
Кривые на рисунке 2.4. сдвинуты относительно друг друга, это отражает температурную зависимость ширины запрещенной зоны. Обычно имеется несколько типов фононов, поэтому при определении коэффициента поглощения проводится суммирование по всем фононным ветвям:

где i – тип фонона.
При выводе выражений (2.58) и (2.59) переход 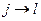 (рисунок 2.2) считался разрешенным, т.е. матричный элемент
(рисунок 2.2) считался разрешенным, т.е. матричный элемент  постоянным (разрешенный переход в виртуальное состояние). Такой переход может быть и запрещенным, тогда
постоянным (разрешенный переход в виртуальное состояние). Такой переход может быть и запрещенным, тогда 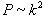 и
и  для непрямых запрещенных межзонных переходов определяется выражением:
для непрямых запрещенных межзонных переходов определяется выражением:
 (2.60)
(2.60)
Непрямые запрещенные переходы практически не проявляются в поглощении, т.к. такие переходы идут не через виртуальные состояния l, а более высокие энергетические состояния.
В сильно легированных полупроводниках с непрямыми переходами сохранение импульса обеспечивается за счет таких процессов рассеяния, как например, электрон – электронное или примесное. В этом случае вероятность рассеяния пропорциональна числу рассеивателей N и участия фонона не требуется.
Все зависимости  были получены лишь для квадратичных законов дисперсии с учетом одной долины. Для Ge, Si,…, SiC и др. полупроводников, имеющих несколько минимумов в зоне проводимости, зависимость
были получены лишь для квадратичных законов дисперсии с учетом одной долины. Для Ge, Si,…, SiC и др. полупроводников, имеющих несколько минимумов в зоне проводимости, зависимость  при энергиях, больших
при энергиях, больших 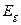 , более сложная.
, более сложная.
2.4 Экситонное поглощение
Теория собственного поглощения, рассмотренная в разделе 2.3, не учитывала кулоновского притяжения в возбужденной электронно-дырочной паре. При поглощении фотона в полупроводниках кулоновское притяжение может привести к образованию возбужденного состояния, в котором электрон и дырка остаются связанными друг с другом в водородоподобном состоянии. Энергия образования этого возбужденного состояния, называемого экситоном, меньше ширины запрещенной зоны, поскольку последняя представляет собой минимальную энергию, требуемую для создания разделенной электронно-дырочной пары и, следовательно, для возникновения фотопроводимости. Экситон может двигаться по кристаллу, фотопроводимость при этом не возникает. В полупроводниках кулоновское притяжение мало, поэтому энергии связи электрона и дырки порядка 0,04 эВ и экситонные орбиты охватывают ряд элементарных ячеек кристалла (радиус орбиты ≈ 15 нм). Такие экситоны хорошо описываются моделью Ваннье, в которой используется приближение эффективной массы; при этом носителям' заряда приписываются эффективные массы, соответствующие краям зоны проводимости и валентной зоны.
Энергия образования экситона определяется формулой
 (2.61)
(2.61)
где  – статическая диэлектрическая проницаемость;
– статическая диэлектрическая проницаемость;
 – приведенная эффективная масса электрона и дырки;
– приведенная эффективная масса электрона и дырки;
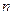 – главное квантовое число для экситона;
– главное квантовое число для экситона;
 – полный волновой вектор, характеризующий движениеэкситона по кристаллу, выражаемый суммой волновых векторов электрона и дырки.
– полный волновой вектор, характеризующий движениеэкситона по кристаллу, выражаемый суммой волновых векторов электрона и дырки.
Второе слагаемое в (2.61) представляет собой кинетическую энергию движения экситона. В частности, при  (покоящийся экситон) получаем набор дискретных "водородных" уровней, отвечающих энергиям возбуждения, меньшим
(покоящийся экситон) получаем набор дискретных "водородных" уровней, отвечающих энергиям возбуждения, меньшим 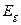 :
:
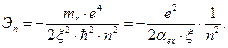 (2.62)
(2.62)
где  – боровский радиус экситона.
– боровский радиус экситона.
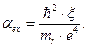 (2.63)
(2.63)
Энергия ионизации экситона определяется выражением
 (2.62)
(2.62)
Таким образом, движение экситона по кристаллу описывается с помощью экситонных зон, однако зависимости  для этих зон нельзя изобразить на обычной диаграмме энергетических зон полупроводника.
для этих зон нельзя изобразить на обычной диаграмме энергетических зон полупроводника.
Оптическим переходам с образованием экситонов обычно соответствуют узкие пики на краю собственного поглощения полупроводников с прямыми переходами или ступеньки на краю поглощения полупроводников с непрямыми переходами. Для вертикальных переходов в  –пространстве должна наблюдаться серия пиков поглощения с энергиями, определяемыми главным квантовым числом:
–пространстве должна наблюдаться серия пиков поглощения с энергиями, определяемыми главным квантовым числом:
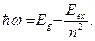 (2.65)
(2.65)
Интенсивность отдельной линии пропорциональна вероятности найти два носителя вместе в связанном состоянии; для разрешенных переходов она убывает по закону 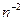 . Эта серия сходится к краю поглощения и в результате перекрытия при больших значениях
. Эта серия сходится к краю поглощения и в результате перекрытия при больших значениях 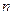 образуется континуум. Интенсивность и спектральная ширина дискретных линий поглощения определяются, в основном, тепловым уширением.
образуется континуум. Интенсивность и спектральная ширина дискретных линий поглощения определяются, в основном, тепловым уширением.
Время жизни экситона может уменьшаться также за счет рассеяния на примесях и дефектах, что приводит к дополнительному уширению линий. В большинстве полупроводников, у которых энергия связи экситона в основном состоянии порядка 4 мэВ, даже при низких температурах наблюдается один пик (рисунок 2.5).
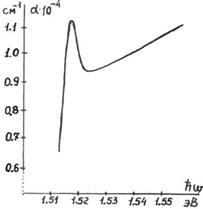
Рисунок 2.5 – Экситонное поглощение в GaAs
В случае непрямых переходов линейчатый спектр экситонов не наблюдается, а наблюдаются ступеньки на краю поглощения. Форма кривой поглощения для низшей экситонной зоны (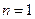 ) определяется плотностью состояний в этой зоне:
) определяется плотностью состояний в этой зоне:
 (2.66)
(2.66)
Поглощение, связанное с зоной 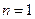 , начинается с зависимости вида
, начинается с зависимости вида
 .
.
Величина коэффициента поглощения определяется выражениями:
 (2.67)
(2.67)
при испускании фононов и при поглощении фононов
 (2.68)
(2.68)
где  – экситонная ширина запрещенной зоны, равная Eg - Ec.
– экситонная ширина запрещенной зоны, равная Eg - Ec.
В общем случае
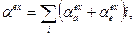
где i – типа фонона.
Структура края поглощения при образовании непрямых экситонов с участием нескольких фононов представлена на рисунке 2.6.

Рисунок 2.6 – Структура края поглощения GaP
При определенных условиях образуются экситоны, локализованные на дефектах различного рода (связанные экситоны). Экситоны локализуются, например, на нейтральных донорах и акцепторах, заряженных донорах.
Наиболее эффективно экситоны локализуются на изоэлектронных ловушках. Изоэлектронные центры образуются в результате замещения атома кристаллической решетки другим атомом с той же валентностью. Примером может служить азот, замещающий фосфор в GaP (или висмут, замещающий галлий в GaP).
Из-за разностей геометрических размеров, псевдопотенциала и электроотрицательностей изоэлектронного центра и замещаемого им элемента решетки, ловушка представляет собой сильно локализованную потенциальную яму. Возникает короткодействующий потенциал, позволяющий нейтральному центру захватить носитель заряда, например, электрон; в результате центр оказывается заряженным. Образующееся кулоновское поле притягивает дырку; два захваченных носителя представляют собой экситон, связанный с изоэлектронной ловушкой. Наиболее хорошо изученной примесью является азот в GaP. В присутствии азота поглощение вблизи основной полосы в GaP очень сильно увеличивается. Связанный экситон не передвигается по кристаллу, поэтому он проявляется в поглощении в виде очень узкой резонансной линии. Кристаллы GaP,содержащие ~ 1019 см-3 азота, вследствие сильного поглощения, обусловленного образованием связанных экситонов, выглядят красными, в то время как обычный материал при 300К имеет медово-желтый цвет.
2.5 Влияние легирования на край собственного поглощения
При легировании полупроводника примесями край собственного поглощения меняется как по форме, так и по энергетическому поглощению вследствие следующих явлений.
1 Экранирование экситонных эффектов. Кулоновское поле между двумя носителями может быть заэкранировано благодаря присутствию других свободных носителей. При высоких концентрациях носителей, когда длина экранирования становится сравнимой с расстоянием между электроном и дыркой, образующими пару, экситонные эффекты весьма сильно ослабляются. При достаточно больших концентрациях примесей

экситонные эффекты исчезают.
2 Сдвиг края собственного поглощения в вырожденном материале (эффект Бурштейна-Мосса). В материале 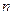 -типа проводимости край собственного поглощения находится при больших энергиях, чем в собственном материале. Из-за достаточно низкой плотности состояний в зоне проводимости относительно малое число электронов может заполнить эту зону, что влияет на край поглощения. Иначе говоря, многие состояния вблизи дна зоны проводимости уже заполнены и не могут принимать электроны, оптически возбужденные из валентной зоны. Этот эффект имеет наибольшую величину в материалах с малой эффективной массой, т.е. как правило в указанных материалах InSb, InAs и др.
-типа проводимости край собственного поглощения находится при больших энергиях, чем в собственном материале. Из-за достаточно низкой плотности состояний в зоне проводимости относительно малое число электронов может заполнить эту зону, что влияет на край поглощения. Иначе говоря, многие состояния вблизи дна зоны проводимости уже заполнены и не могут принимать электроны, оптически возбужденные из валентной зоны. Этот эффект имеет наибольшую величину в материалах с малой эффективной массой, т.е. как правило в указанных материалах InSb, InAs и др.
3 Переходы в "хвосты" плотности состояний. При оптических переходах с участием "хвостов" плотности состояний энергия соответствующих фотонов  может оказаться меньше
может оказаться меньше 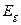 . О поглощении таких фотонов говорят как о "хвосте" поглощения или оптическом "хвосте". Поглощение в "хвосте" плотности состояний объясняется эффектами туннелирования.
. О поглощении таких фотонов говорят как о "хвосте" поглощения или оптическом "хвосте". Поглощение в "хвосте" плотности состояний объясняется эффектами туннелирования.
4 Рассеяние квазиимпульса на примесях и свободных носителях заряда. В спектре собственного поглощения при непрямых переходах появляется бесфононный компонент в поглощении:
 .
.
При большой концентрации примесей возможны процессы рассеяния квазиимпульса при прямых переходах, что сказывается на форме края поглощения.
2.6 Примесное поглощение
Виды оптического поглощения с участием примесей приведены на рисунке 2.7.
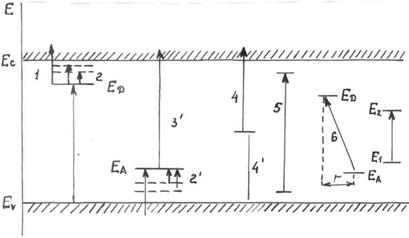
Рисунок 2.7 – Схема электронных переходов для примесного поглощения
1,1 – фотононизация мелких доноров и акцепторов (1 – переход дырок);
2,2 – фотовозбуждение доноров и акцепторов (2 –переход для дырок);
3,3' – фотонейтрализация доноров и акцепторов;
4,4' – фотононизация глубоких центров;
5 – оптическое поглощение на связанном экситоне;
6 – межпримесное оптическое поглощение;
7 – внутрицентровые переходы.
Простейший вид поглощения, связанного с примесными уровнями – переход электрона из основного состояния в возбужденное состояние нейтральной примеси. Такое поглощение обычно наблюдается при энергиях фотона, значительно меньших энергии края поглощения. Возбуждение электронов примеси, т.е. перевод электрона из основного состояния в какое-либо из возбужденных состояний приводит к появлению линейчатого спектра поглощения. Так на типичной кривой поглощения для Si с примесью B четко выступают три линии поглощения, обусловленные возбуждением электрона с основного уровня (рисунок 2.8).
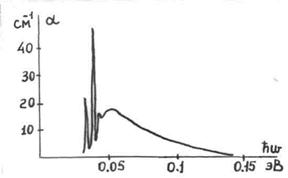
Рисунок 2.8 – Зависимость коэффициента поглощения для образца кремния, легированного бором, от энергии фотона
Наблюдаются пики поглощения, связанные с переходами в состояния с  Пики с большими энергиями сливаются с полосой, соответствующей полной ионизации донора. Уменьшение коэффициента поглощения при энергиях фотона, больших энергии ионизации донора обусловлено тем, что донор занимает ограниченный участок пространства квазиимпульсов.
Пики с большими энергиями сливаются с полосой, соответствующей полной ионизации донора. Уменьшение коэффициента поглощения при энергиях фотона, больших энергии ионизации донора обусловлено тем, что донор занимает ограниченный участок пространства квазиимпульсов.
Переходы 3,3' проявляются в компенсированных полупроводниках. Энергии переходов принимают значения вблизи края собственного поглощения, как показано на рисунке 2.9, где неглубокие акцепторный и донорный уровни представлены отрезками горизонтальных прямых.

Рисунок 2.9 – Схема электронных переходов, обуславливающих фотонейтрализацию примесных центров
По сравнению с донорным акцепторное состояние размазано в  – пространстве из-за большей
– пространстве из-за большей 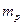 . Переходы из зоны тяжелых дырок на ионизированные доноры должны давать резкий пик поглощения при энергиях меньших, чем у края собственного поглощения.
. Переходы из зоны тяжелых дырок на ионизированные доноры должны давать резкий пик поглощения при энергиях меньших, чем у края собственного поглощения.
Для наблюдения такого пика требуются обычно очень низкие температуры для устранения уширения линии, вызванного рассеянием на фононах, но понижение температуры приводит также к заселению донорных уровней электронами. Кроме того, концентрация доноров должна быть невелика, чтобы не происходило образования примесной зоны. Переходы между акцепторными уровнями и зоной проводимости должны проявляться в виде уступа или ступеньки на краю поглощения, с порогом при энергии 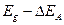 , как это показано на рисунке 2.10.
, как это показано на рисунке 2.10.
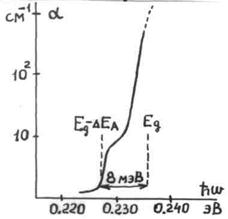
Рисунок 2.10 – Примесное поглощение в JnSb, легированном цинком и кадмием
На практике поглощение, связанное с мелкими примесями, трудно выделить на фоне поглощения, связанного с переходами между хвостами зон.
При участии в процессах оптического поглощения глубоких примесей форма спектра поглощения определяется, в основном, электрон-фононным взаимодействием, характерны широкие безструктурные полосы.
В компенсированных полупроводниках возможны переходы из акцепторных состояний в донорные. Такие переходы отчетливо проявляются в излучательной рекомбинации.
Внутрицентровые переходы наблюдаются при легировании полупроводника элементами с незастроенными внутренними оболочками, например, элементами группы железа, лантаноидами. Полупроводник выполняет роль матрицы, а переходы происходят между внутренними состояниями одного и того же атома или иона, аналогично тому, как они происходят в свободных, изолированных атомах или ионах.
2.7 Оптическое поглощение при внутризонных переходах
В полупроводниках n-типа возможны внутризонные переходы между различными подзонами зоны проводимости и в пределах той же долины (рисунок 2.11).

Рисунок 2.11 – Спектр поглощения GaP 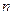 -типа
-типа
1 – прямые внутризонные переходы в точке (100) между минимумами подзон x1 и х3;
2 – переходы внутри той же долины;
3 – непрямые внутризонные переходы между минимумами подзон х1 и Г1;
4,5 – фотононизация доноров при переходах в подзоны x1 и х3 .
Переходы (3) – непрямые и характеризуются меньшей вероятностью, чем переходы типа (1). При низких температурах спектр поглощения, обусловленный внутризонными переходами (1) трансформируется в спектр примесного поглощения – переходы (4) и (5).
Внутризонные переходы между различными подзонами зоны проводимости наблюдаются также в AlSb, GaAs, SiC.
В полупроводниках р -типа, где потолок валентной зоны занят дырками, возможны три типа переходов, обусловленных поглощением фотонов (рисунок 2.12):
1 – из зоны легких дырок 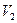 в зону тяжелых дырок
в зону тяжелых дырок  ;
;
2 – из зоны 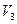 , отщепленной за счет спин-орбитального взаимодействия, в зону тяжелых дырок
, отщепленной за счет спин-орбитального взаимодействия, в зону тяжелых дырок  ;
;
3 – из отщепленной зоны 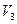 в зону легких дырок в
в зону легких дырок в 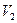 .
.

Рисунок 2.12 – Внутризонные переходы в полупроводниках р -типа
2.8 Поглощение свободными носителями
Поглощение свободными носителями заряда наблюдается при переходах в пределах одной долины (рисунок 2.11, переход 2). Такие переходы являются непрямыми и возможны при наличии рассеяния.
Поглощение свободными носителями характеризуется монотонным, часто безструктурным спектром, описываемым законом  , где
, где 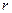 меняется от 1.5 до 3.5:
меняется от 1.5 до 3.5:
 (2.69)
(2.69)
где A, B, C – константы;
 – при рассеянии акустическими фононами;
– при рассеянии акустическими фононами;
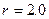 – оптическими фононами;
– оптическими фононами;
 – ионизированными примесями.
– ионизированными примесями.
2.9 Решеточное поглощение
Оптическое поглощение на колебаниях решетки происходит в результате взаимодействия электромагнитного поля световой волны с движущимися зарядами узлов решетки. Энергия фотона  передается решетке, увеличивая ее колебания. Решеточное поглощение характеризуется рядом пиков, лежащих в инфракрасной области спектра.
передается решетке, увеличивая ее колебания. Решеточное поглощение характеризуется рядом пиков, лежащих в инфракрасной области спектра.
2.10 Спектры собственного поглощения кристаллов кремния, германия и арсенида галлия
На рисунке 2.13 показан спектр собственного поглощения кремния, вид которого характерен вообще для чистых полупроводников. Коэффициент поглощения d изменяется в пределах многих порядков величины. В твердом теле имеется множество заполненных и свободных энергетических зон, каждая из которых в свою очередь состоит из нескольких подзон, поэтому в спектрах собственного поглощения наблюдается ряд широких полос со структурой, что определяется сложным строением каждой из зон.

Рисунок 2.13 – Спектр собственного поглощения нелегированного кремния
Минимальная энергия фотонов, при которой начинается собственное поглощение в идеальных кристаллах, определяется шириной запрещенной зоны  полупроводника или диэлектрика. Область вблизи
полупроводника или диэлектрика. Область вблизи  называется краем собственного (фундаментального) поглощения. Край поглощения кремния обусловлен непрямыми переходами. Прямые переходы наблюдаются при
называется краем собственного (фундаментального) поглощения. Край поглощения кремния обусловлен непрямыми переходами. Прямые переходы наблюдаются при  (рисунок 2.13). При более высоких энергиях оптические свойства кремния определяются электронами валентной зоны, которые ведут себя как плазма электронов с эффективной массой, равной единице, и малым временем релаксации. При еще более высоких энергиях возбуждаются электроны из глубоких зон, в случае кремния – из 2 р – зоны.
(рисунок 2.13). При более высоких энергиях оптические свойства кремния определяются электронами валентной зоны, которые ведут себя как плазма электронов с эффективной массой, равной единице, и малым временем релаксации. При еще более высоких энергиях возбуждаются электроны из глубоких зон, в случае кремния – из 2 р – зоны.
На рисунке 2.14 показан спектр собственного поглощения арсенида галлия, полупроводника с прямой структурой зон.

Рисунок 2.14 – Край собственного поглощения в арсениде 1.2 галлия при комнатной температуре
Теоретически в соответствии с выражением (2.51) коэффициент поглощения должен обращаться в нуль при  ,тогда как на практике, как это видно рисунке 2.14, коэффициент поглощения остается довольно значительным даже при
,тогда как на практике, как это видно рисунке 2.14, коэффициент поглощения остается довольно значительным даже при  и убывает с уменьшением энергии фотона приблизительно по экспоненциальному закону. Экспоненциальный край поглощения в GaAs можно объяснить переходами между хвостами зон, форма и величина которых зависят от легирования материала.
и убывает с уменьшением энергии фотона приблизительно по экспоненциальному закону. Экспоненциальный край поглощения в GaAs можно объяснить переходами между хвостами зон, форма и величина которых зависят от легирования материала.
Спектр собственного поглощения германия приведен на рисунке 2.15.
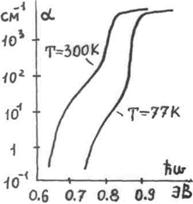
Рисунок 2.15 – Край собственного поглощения в германии при температуре 77 и 300 К
Край собственного поглощения в германии, как и в кремнии, обусловлен непрямыми переходами. Перегиб на кривых при 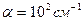 указывает на переход от непрямого к прямому поглощению (~0.8 эВ при Т = 300 К).
указывает на переход от непрямого к прямому поглощению (~0.8 эВ при Т = 300 К).
2.11 Край собственного поглощения полупроводниковых твердых растворов
Кроме бинарных соединений элементов III и V групп, таких как GaAs, InP, GaP, AlAs и др., большое значение для оптоэлектроники имеют твердые растворы на их основе. Принципиально важной особенностью твердых растворов является возможность плавно и в широких пределах изменять параметры материала путем изменения его состава, что позволяет получать материал с точно заданным набором основных характеристик.
Образование твердых растворов в полупроводниках группы  возможно при замещении как анионной, так и катионной подрешеток, например, трехкомпонентные растворы в системах GaAs-GaP(GaAs1-x Px), GaAs-AlAs(Gax Al1-x As), InP-GaP(In1-x Gax P).
возможно при замещении как анионной, так и катионной подрешеток, например, трехкомпонентные растворы в системах GaAs-GaP(GaAs1-x Px), GaAs-AlAs(Gax Al1-x As), InP-GaP(In1-x Gax P).
Возможны и четырехкомпонентные твердые растворы типа Gax In1-x AsyP1-y.
На рисунке 2.16 приведены упрощенные энергетические диаграммы для электронных состояний в кристаллах арсенида галлия и фосфида галлия.
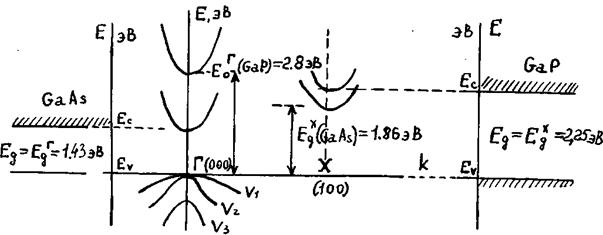
Рисунок 2.16 – Упрощенные энергетические диаграммы арсенида 1.4 галлия и фосфида галлия
Энергетические зазоры, отсчитанные от потолка валентной зоны до одного из минимумов зоны проводимости, обозначены символом  с соответствующим индексом сверху, как показано на рисунке 2.16. В арсениде галлия абсолютный минимум зоны проводимости и максимум валентной зоны совпадают в
с соответствующим индексом сверху, как показано на рисунке 2.16. В арсениде галлия абсолютный минимум зоны проводимости и максимум валентной зоны совпадают в  – пространстве: оба они находятся в центре зоны Бриллюэна (состояние
– пространстве: оба они находятся в центре зоны Бриллюэна (состояние  , обозначенное Г). Ширина запрещенной зоны
, обозначенное Г). Ширина запрещенной зоны  соответствует минимальному энергетическому зазору
соответствует минимальному энергетическому зазору  , называемому прямым. Таким образом, арсенид галлия является полупроводником с прямой структурой зоны. Величина непрямого энергетического зазора
, называемому прямым. Таким образом, арсенид галлия является полупроводником с прямой структурой зоны. Величина непрямого энергетического зазора  для GaAs составляет 1.86 эВ. Точка х – (100), является точкой пересечения оси
для GaAs составляет 1.86 эВ. Точка х – (100), является точкой пересечения оси 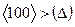 с границей зоны Бриллюэна. Полупроводники группы A3B5 GaAs и GaP обладают сходной структурой валентной зоны. Для фосфида галлия минимальный энергетический зазор
с границей зоны Бриллюэна. Полупроводники группы A3B5 GaAs и GaP обладают сходной структурой валентной зоны. Для фосфида галлия минимальный энергетический зазор  непрямой, таким образом, GaP является полупроводником с непрямой структурой зон. Ширина запрещенной зоны фосфида галлия
непрямой, таким образом, GaP является полупроводником с непрямой структурой зон. Ширина запрещенной зоны фосфида галлия 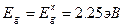 . Параметры зонной структуры плавно изменяются с изменением состава твердого раствора GaAs1-x Px. Наиболее важным является характер изменения соответствующих энергетических зазоров в зависимости от состава твердого раствора. На рисунке 2.17 показан характер изменения энергетических зазоров в твердом растворе GaAs1-x Px.
. Параметры зонной структуры плавно изменяются с изменением состава твердого раствора GaAs1-x Px. Наиболее важным является характер изменения соответствующих энергетических зазоров в зависимости от состава твердого раствора. На рисунке 2.17 показан характер изменения энергетических зазоров в твердом растворе GaAs1-x Px.
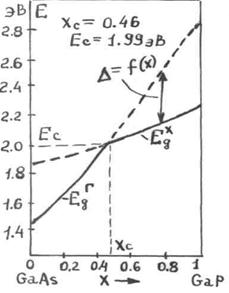
Рисунок 2.17 – Изменение "прямого" ( ) и "непрямого"
) и "непрямого"  , энергетических зазоров в твердом растворе GaAs1-x Px
, энергетических зазоров в твердом растворе GaAs1-x Px
Для кристаллов GaAs1-x Px при  – минимум зоны проводимости расположен ниже х – минимума, и эти твердые растворы имеют "прямую" структуру зон. Твердые растворы GaAs1-x Px при
– минимум зоны проводимости расположен ниже х – минимума, и эти твердые растворы имеют "прямую" структуру зон. Твердые растворы GaAs1-x Px при  имеют "непрямую" структуру зон. Состав твердого раствора, при котором происходит переход от "прямой" к "непрямой" структуре энергетических зон, называется переходным. В точке перестройки зонной структуры
имеют "непрямую" структуру зон. Состав твердого раствора, при котором происходит переход от "прямой" к "непрямой" структуре энергетических зон, называется переходным. В точке перестройки зонной структуры 
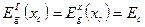 .
.
Характеристики энергетической зонной структуры некоторых полупроводниковых твердых растворов приведены в таблице 2.1.
Таблица 2.1 – Значения ширины запрещенной зоны (в электронволътах) и состава, соответствующих переходу к непрямозонному полупроводнику, для некоторых тройных твердых растворов соединений типа A3B5 (при 300 К)
| Твердый раствор |  , эВ , эВ
|  , эВ , эВ
|  , эВ , эВ
| 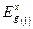 , эВ , эВ
|  , эВ , эВ
| 
|
| GaAs1-x Px | 1,43 | 2,78 | 1,86 | 2,27 | 1,99 | 0,46 |
| AlxGa1-хAs | 1,43 | 3,10 | 1,86 | 2,16 | 2,02 | 0,37 |
| Jn1-x Gax P | 1,34 | 2,78 | 2,17 | 2,26 | 2,18 | 0,72 |
| Jn1-x Alx P | 1,34 | 3,70 | 2,17 | 2,45 | 2,33 | 0,44 |
Примечание: индекс (о) означает прямую, a (1) – непрямую структуру энергетических зон.
В полупроводниковых твердых растворах с изменением их состава край собственного поглощения будет сдвигаться по энергии в соответствии с изменением ширины запрещенной зоны:

(см. также рисунок 2.17).
На рисунке 2.18 приведены экспериментальные данные по краю собственного поглощения кристаллов GaAs1-x Px.

Рисунок 2.18 – Край собственного поглощения твердых растворов
GaAs1-x Px при Т=4.2 К для различных составов х
В области составов край поглощения определяется прямыми переходами, а в области
край поглощения определяется прямыми переходами, а в области  – непрямыми переходами в экситонные состояния. Кроме переходов с участием фононов наблюдаются непрямые переходы без участия фононов, пороговая энергия для которых равна экситонной ширине запрещенной зоны. Бесфононный компонент обозначен на рисунке сплошной линией. Его интенсивность возрастает при уменьшении X. Форма края собственного поглощения в области прямых межзонных переходов не претерпевает существенных изменений по сравнению с бинарными соединениями
– непрямыми переходами в экситонные состояния. Кроме переходов с участием фононов наблюдаются непрямые переходы без участия фононов, пороговая энергия для которых равна экситонной ширине запрещенной зоны. Бесфононный компонент обозначен на рисунке сплошной линией. Его интенсивность возрастает при уменьшении X. Форма края собственного поглощения в области прямых межзонных переходов не претерпевает существенных изменений по сравнению с бинарными соединениями  . Определяющую ро
. Определяющую ро
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 5039; Нарушение авторских прав?; Мы поможем в написании вашей работы!