Точность работы САУ в установившемся режиме

Лекция 20

В общем случае на САУ оказывают влияние задающее воздействие v(t), возмущающее воздействие f(t) и шум измерения s(t). При этом изображение по Лапласу у(р) выходной величины y(t) линейной системы может быть записано в виде

y(p)=Ф(p)v(p)+Ф_f(p)f(p)+Ф_s(p)s(p), (1)

где

Ф(р) – передаточная функция замкнутой системы,

Ф_f(p) – передаточная функция по возмущению f(p)=L{f(t)},

Ф_s(p) – передаточная функция по шуму измерения s(p)=L{s(t)},

v(p)=L{v(t)} - изображение по Лапласу задающего воздействия v(t).

Заметим, что для системы с одной степенью свободы (см. рисунок ниже) у(р) можно выразить как

y(p)=T(p)[v(p) - s(p)]+ W₁(p)S(p)f(p),

используя передаточную функцию объекта W₁(p), функцию чувствительности S(p) и дополнительную функцию чувствительности T(p).

Задачей САУ является обеспечение в любой момент времени равенства величин: y(t)=v(t). Однако реальная система выполняет эту задачу с некоторой ошибкой

ε_п(t)=v(t) -y(t) (2)

равной разности между заданным v(t) и действительным y(t) значениями управляемой величины. Изображение по Лапласу этой ошибки с учетом (1) равно

ε_п(р)=v(p)-y(p)= ε(p)+ ε_f(p)+ ε_s(p), (3)

где

ε(p)=[1-Ф(p)]v(p), (4)

ε_f(p)=-Ф_f(p)f(p), (5)

ε_s(p)=-Ф_s(p)s(p). (5,а)

Для системы с одной степенью свободы

ε(p)=S(p)v(p),

ε_f(p)= -W₁(p)S(p)f(p),

ε_s(p)=-T(p)s(p),

и полная ошибка

ε_п(р)= S(p)v(p) - W₁(p)S(p)f(p)+ T(p)s(p)

зависит от функции чувствительности S(p) и дополнительной функции чувствительности S(p).

· Для хорошего воспроизведения сигнала v ( обычно низкочастотного ) требуется

| S(j)| было малым 0.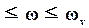

· Для снижения влияния шума измерения (шума датчика) s ( обычно высокочастотного) требуется

|T(j)| было малым .

Т.к. T(p)+ S(p)=1 p, то мы не можем сделать так, чтобы обе T(p) и S(p) были малыми на тех же самых (одинаковых частотах) (см. рисунок ниже).

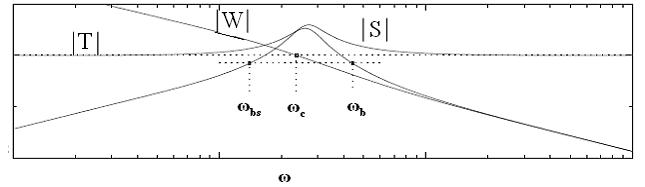
Это обстоятельство является фундаментальным ограничением при проектировании системы.

Таким образом, ошибка системы состоит из трех составляющих

ε_п(t)= ε(t)+ ε_f(t)+ ε_s(t), (6)

первая из которых ε(t)=L^-1[ε(p)] называется ошибкой воспроизведения, вторая ε_f(t)=L^-1[ε_f(p)] - ошибкой по возмущению, а третья ε_s(t)=L^-1[ε_s(p)] – ошибкой по шуму измерения.

Ошибка воспроизведения показывает, как точно воспроизводит данная система задающее воздействие v(t) в отсутствие других внешних воздействий (f=s=0). Величина этой ошибки определяется инерционностью системы и видом задающего воздействия v(t).

Ошибки по возмущению и шуму измерения соответственно показывают, как влияют на управляемую величину возмущение и шум измерения при задающем воздействии v(t), равном нулю. Такое разделение ошибки на три составляющие возможно лишь в линейных системах, для которых справедлив принцип суперпозиции.

Выражение (6) для устойчивых систем определяет ошибку как в установившемся, так и в переходном режимах. Переходная составляющая ошибки обычно рассматривается при исследовании переходных процессов. Поэтому в данной главе остановимся на рассмотрении ошибки в установившемся режиме, который теоретически наступает при t→∞. Величина установившейся ошибки

(ε_п)_уст(t)= ε_уст(t)+ (ε_f)_уст(t)+ (ε_s)_уст(t) (7)

характеризует точность работы САУ в установившемся режиме.

Рассмотрим методы вычисления установившейся ошибки воспроизведения ε_уст(t) и установившейся ошибки по возмущению (ε_f)_уст(t).

Ошибка воспроизведения.

Установившееся значение ошибки воспроизведения в ряде случаев определяется с помощью известной в операционном исчислении теоремы о конечном значении, которая применительно к данному случаю может быть записана в виде

ε_уст= . (8)

Преобразование Лапласа ε(р) ошибки легко найти, если известны преобразование Лапласа v(р) входного сигнала и передаточная функция для ошибки Ф_ε(р), связанная с передаточной функцией Ф(р) замкнутой системы соотношением

Ф_ε(р)=1 - Ф(р). (9)

Действительно, согласно (4)

ε(р)=Ф_ε(р)v(p). (10)

Принимая во внимание существующую для системы с одной степенью свободы связь между передаточными функциями замкнутой Ф(р) и разомкнутой W(р) систем

Ф(р)=T(p)=W(p)/(1+W(p)),

а также, что

_,

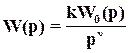на основании (9) имеем

Ф_ε(р)=1-T(p)=S(p)=.

Поэтому передаточная функция по ошибке называется также функцией чувствительности.

Следовательно,

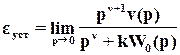. (11)

Учитывая, что W₀(p) обладает свойством W₀(0)=1, получаем

. (12)

Выражение (12) имеет смысл, если ε(t) стремится к определенному пределу при t→∞. В противном случае выражение (8) неприменимо. Рассмотрим от каких факторов зависит ошибка ε_уст при типовых входных сигналах, для которых вышеуказанное требование соблюдается.

Входной сигнал – ступенчатая функция v ( t)=a₀1(t).

Операторное выражение такой функции v(p)=a₀/p. При этом

(13)

Если ν=0 (система не содержит интегрирующих звеньев), то

(14)

Следовательно, в такой системе, даже при постоянном входном сигнале, имеет место ошибка, называемая ошибкой по положению или статической ошибкой. Ошибка 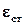при известном а₀ определяется статизмом системы

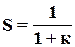(15)

и она тем меньше, чем больше коэффициент усиления k ( рис. a ниже).

Системы, обладающие статической ошибкой, называются статическими системами. Коэффициент усиления k статических систем является безразмерной величиной, так как величины а₀ и ε_уст имеют одинаковую размерность.

Отметим, что статическая ошибка, определяемая выражением (14), является принципиальной (методической) ошибкой и обусловлена принципом действия системы.

Если ν>1 (система содержит одно или несколько интегрирующих звеньев), то, как это видно из выражения (13), статическая ошибка равна нулю. Системы, обладающие нулевой статической ошибкой, называются астатическими системами (рис b ниже). При этом величина ν, как говорят, определяет порядок астатизма системы.

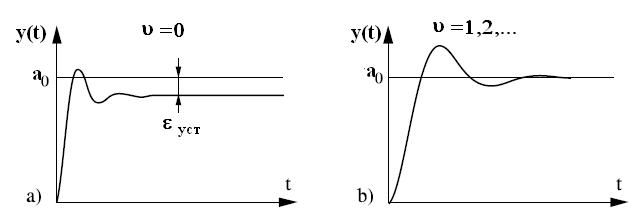
Астатическую систему можно рассматривать как статическую систему с бесконечно большим коэффициентом усиления k. Действительно, наличие интегрирующих звеньев приводит к тому, что при постоянном входе сигнал на выходе разомкнутой системы с течением времени растет до бесконечности.

Входной сигнал v(t)=a₁t, изменяющийся с постоянной скоростью a₁.

В этом случае v(p)=a₁/p², а установившаяся ошибка

. (16)

Если ν=0 (статическая система), то ε_уст=∞. Полученному результату легко дать объяснение, если учесть, что в установившемся режиме, т.е. при t→∞, на входе системы имеется бесконечно большой сигнал и поэтому при конечном коэффициенте усиления k, согласно (14), ошибка ε_уст равна бесконечности. Другими словами, данный случай можно рассматривать как предыдущий при v(t)=a₀, если положить a₀=∞.

Если ν=1 (система с астатизмом первого порядка), то

. (17)

При этом ошибка ε_уст обратно пропорциональна коэффициенту усиления и носит название скоростной ошибки. Так как входной сигнал v и ошибка ε имеют одинаковую размерность, то коэффициент усиления системы с астатизмом первого порядка имеет размерность [сек^-1] и характеризует установившуюся скорость изменения выходной величины разомкнутой системы при постоянном входном сигнале.

Физический смысл полученного результата виден на примере простейшей следящей системы (рис. 1). Если на входе имеем сигнал v, изменяющийся с постоянной линейной скоростью a₁, то установившийся режим будет иметь место лишь в случае, когда выходная величина у будет изменяться с той же скоростью а₁.

Рис. 1

Но для этого необходимо подвести к двигателю определенное напряжение u=a₁/k_дв, зависящее от коэффициента усиления двигателя k_дв. Это напряжение может появиться только при наличии сигнала ошибки ε_уст. Чем больше коэффициент усиления усилителя k_ус, а следовательно, и всей системы – k=k_усk_дв, тем меньшее значение ε_уст=а₁/k требуется для вращения двигателя со скоростью, равной скорости изменения входного сигнала.

Используя выражение (17), по заданным значениям скорости а₁₀ и скоростной ошибки (ε_ск)_доп можно найти величину коэффициента усиления

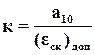. (18)

обеспечивающую требуемую точность воспроизведения сигнала v(t)=a₁₀t.

Если ν≥2 (система с порядком астатизма выше первого), то скоростная ошибка равна нулю.

Дата добавления: 2014-01-07