Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси

Рассмотрим твердое тело, вращающееся вокруг неподвижной оси Z с угловой скоростью ω (рис. 175). 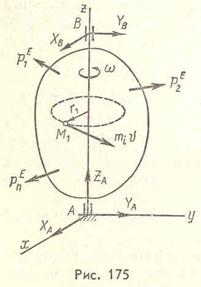Вычислим кинетический момент этого тела относительно оси его вращения. Момент количества движения точки М_i - тела относительно оси Z: 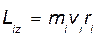(a)

где 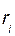- радиус окружности, описываемой точкой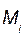; 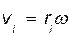- алгебраическая величина вращательной скорости точки 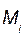. Подставляя в (а) это значение 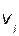получаем .

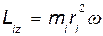Кинетический момент твердого тела относительно оси Z: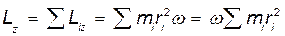

Здесь 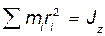- момент инерции твердого тела относительно оси Z. Таким образом (79.1)

т. е. кинетический момент вращающегося твердого тела относительно неподвижной оси его вращения равен произведению момента инерции тела относительно той же оси на угловую скорость тела.

Рассмотрим изменение кинетического момента тела относительно оси Z под действием приложенных к нему задаваемых внешних сил 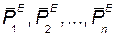. Теорема об изменении кинетического момента механической системы выражается уравнением (56.2):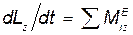

Реакции подшипника В и подпятника А являются внешними силами, но при отсутствии трения их моменты относительно оси Z равны нулю, и правая часть уравнения (56.2) содержит только сумму моментов задаваемых внешних сил. При наличии трения эта сумма содержит также момент сил трения. Так как по (79.1)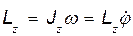

То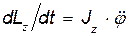

а потому уравнение (56.2) принимает вид 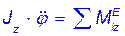(79.2)

Уравнение (79.2) представляет собой дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

Сравним уравнение (79.2) с дифференциальным уравнением поступательного прямолинейного движения твердого тела: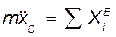

Очевидно, что момент инерции твердого тела при вращательном движении имеет то же значение, что и масса тела при его поступательном движении: момент инерции является характеристикой инертности тела при вращательном движении.

Если вращение тела происходит в одном направлении, то это направление считают положительным. В этом случае моменты движущих сил положительны, моменты сил сопротивления отрицательны, а главный момент внешних сил может иметь тот или другой знак.

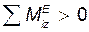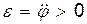Если , то , т. е. тело вращается ускоренно.

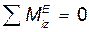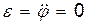Если , то ; и 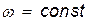, т.е. вращение тела равномерное.

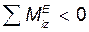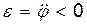Если , то , т. е. тело вращается замедленно.

По дифференциальному уравнению (79.2) можно решать следующие задачи:

1) по заданному уравнению вращения тела 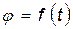и его моменту инерции J_z определять главный момент внешних сил, действующих на тело:

2) по заданным внешним силам, приложенным к телу, по начальным условиям вращения 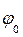и и по моменту инерции тела J_z находить уравнение вращения тела ;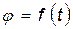

3) определять момент инерции тела J_z относительно оси вращения, зная величины 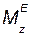и .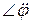

Дата добавления: 2014-01-07