Однородные уравнения. Определение: Дифференциальное уравнение первого порядка называется однородным, если его можно представить в виде: (12)

Определение: Дифференциальное уравнение первого порядка называется однородным, если его можно представить в виде:

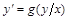
(12)

Понятие однородного дифференциального уравнения связано с понятием однородной функции. Функция 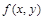называется однородной степени k, если для произвольного числа a выполняется равенство .

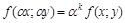Метод решения однородных дифференциальных уравнений основан на введении замены вида:

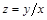
(13)

В этом случае производная от функции y равна

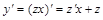
(14)

. Поэтому уравнение (12) можно представить в виде:

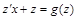
(15)

Это уравнение с разделяющимися переменными и его можно записать в виде:

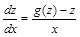
(16)

Пример 4. Решить уравнение .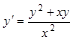

Решение: Это однородное уравнение, так как его можно записать в виде: (*).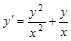

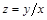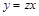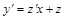Введем замену (**). Тогда и (***). Подставим выражения (**) и (***) в уравнение (*):

;

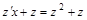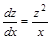- это уравнение с разделяющимися переменными. Умножаем обе части на dx и делим на :

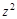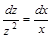. Интегрируем обе части уравнения:

;

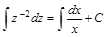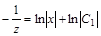, где .

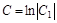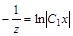или .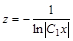

Подставим вместо z выражение (**):

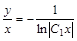или 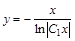. Это общее решение исходного однородного уравнения.

Неполные уравнения

Определение. Дифференциальное уравнение первого порядка называется неполным, если в него кроме производной 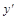входит либо только аргумент 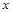, либо только функция .

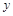Если в уравнение кроме производной входит только аргумент функции, то такое неполное уравнение можно записать в виде:

.

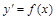Оно решается разделением переменных:

;

;

.

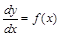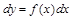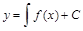(17)

Если в уравнение кроме производной входит только функция y, то такое неполное уравнение можно записать в виде:

.

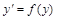Оно решается также разделением переменных:

;

;

.

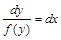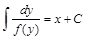(18)

Линейные уравнения первого порядка

Определение. Уравнение вида:

,

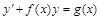(19)

где 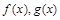- непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Неизвестная функция и ее производная входят в уравнение в первой степени – линейно, то и объясняет название уравнения.

Если 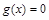, то уравнение (19) называют линейным однородным.; если 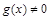, то уравнение (19) называют линейным неоднородным.

Замечание: не путать однородные ДУ и линейные однородные ДУ.

Линейные однородные уравнения решаются путем разделения переменных:

;

;

;

.

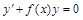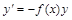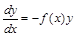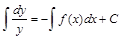Линейные неоднородные уравнения решаются следующим методом.

Решение будем искать в виде:

.

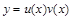(20)

Функция 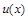- может быть выбрана произвольно, а 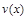должна определяться из уравнения (19).

Продифференцируем левую и правую части выражения (20):

.

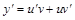(21)

Подставим выражения (20) и (21) в уравнение (19):

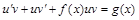
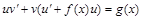
(22)

Сначала найдем какое-либо частное решение 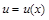уравнения:

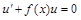
(23)

Тогда функция 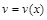будет находится из уравнения:

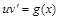
(24)

Таким образом решение исходного линейного неоднородного уравнения (19) сводится к решению двух уравнений с разделяющимися переменными (23) и (24).

Пример 5. Найти общее решение дифференциального уравнения .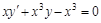

Решение: Перенесем слагаемое 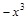в правую часть уравнения и поделим обе части на :

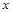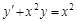- это линейное неоднородное уравнение (*).

Решение будем искать в виде:

.

(**)

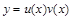Тогда

.

(***)

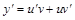Подставим выражения (**) и (***) в уравнение (*):

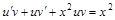. Сгруппируем первое и третье слагаемые в левой части уравнения:

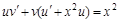.(****). Подберем такое 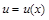, чтобы множитель 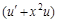обращался в нуль. Для этого найдем частное решение уравнения:

;

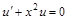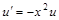- это уравнение с разделяющимися переменными.

;

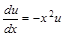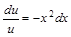. Проинтегрируем обе части уравнения:

.

.

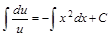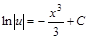Выберем частное решения этого уравнения при C=0:

;

.

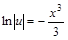Подставляя полученное значение для в уравнение (****), получим уравнение вида:

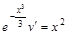. Поделим обе части уравнения на :

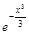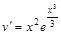- это неполное уравнение.

.

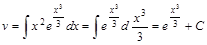Таким образом, решением исходного уравнения будет функция: .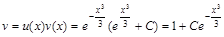

Некоторые нелинейные уравнения приводятся к линейным соответствующими заменами неизвестной функции 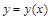. К таковым относится уравнение Бернулли:

,

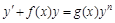(25)

где 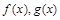- непрерывные функции, а 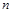- некоторое постоянное число.

Пусть 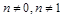. Введем новую функцию:

,

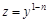(26)

тогда получим линейное дифференциальное неоднородное уравнение относительно неизвестной функции :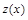

.

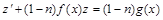(27)

Пример 6. Найти общее решение дифференциального уравнения .

Решение: Это уравнение Бернулли при 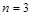. Сделаем замену:

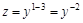
В этом случае получим линейное уравнение:

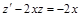
Будем искать решение уравнения в виде: 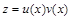, тогда.

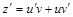Подставим замену в уравнение:

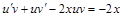. Сгруппируем первое и третье слагаемые:

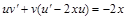. Решаем уравнение:

;

;

;

;

;

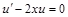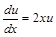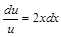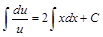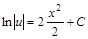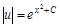. Выберем частное решение при C=0:

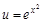. Подставим данное значение в уравнение:

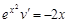. Поделим обе части на :

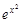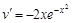- это неполное уравнение.

.

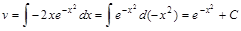Найдем функцию ..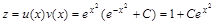

Выполняем обратную замену: .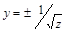

.

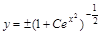Дата добавления: 2014-01-07