Дослід Франка і Герца

Німецькі фізики Д. Франк і Г. Герц експериментально довели дискретність значень енергій атомів, вивчаючи методом затримуючого потенціалу зіткнення електронів з атомами газів. Схема їх установки наведена на рис. 4.1.

Трубка, яка заповнена парами ртуті при низькому тиску (~130 Па), містить катод K, анод A і сітку C. Електрони, які вилітають з катода внаслідок термоелектронної емісії, прискорюються різницею потенціалів U, що прикладена між катодом і сіткою. Цю різницю потенціалів можна змінювати за допомогою потенціометра П. Між сіткою С і анодом А прикладена гальмівна різниця потенціалів порядку 0,5 В. Д. Франк і Г. Герц досліджували залежність сили струму І в колі анода від напруги U між катодом і сіткою. Сила струму вимірювалась гальванометром G, напруга – вольтметром V.

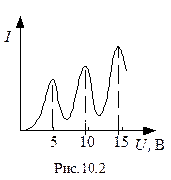Електрони в області між катодом і сіткою співударяються з атомами парів ртуті. Ті електрони, які після співударів мають достатню енергію, щоб подолати гальмівне поле, досягають анода. При непружних ударах електронів з атомами ртуті останні можуть збуджуватися. Згідно з теорією Бора кожен з атомів ртуті може отримати лише певну енергію, переходячи при цьому в один із збуджених станів. Тому, якщо в атомах дійсно існують стаціонарні стани, то електрони, стикаючись з атомами ртуті, повинні втрачати енергію дискретно, певними порціями, які дорівнюють різниці енергій відповідних стаціонарних станів атома.

При збільшенні напруги до 4,86 В, сила анодного струму зростає монотонно, проходить через максимум (4,86 В), потім різко падає і зростає знову (рис. 10.2). Наступні максимуми спостерігаються при 2·4,86 B і 3·4,86 B.

Доки напруга між катодом K і сіткою C менша, ніж 4,86 В, то електрони, зустрічаючи на своєму шляху атоми ртуті, взаємодіють пружно. При eU= 4,86 eB енергія електрона достатня, щоб викликати непружний удар, при якому електрон віддає атому ртуті всю кінетичну енергію, збуджуючи перехід одного з електронів атома на вищий енергетичний рівень, тобто атом переходить у збуджений стан. Електрони, які втратили свою кінетичну енергію, уже не зможуть подолати гальмівного поля і досягнути анода. При значеннях енергій, кратних 4,86 еВ, електрони можуть 2,3,... рази співударятися непружно з атомами ртуті, втрачаючи при цьому повністю свою енергію, і не долетять до анода.

Досліди Франка і Герца показали, що електрони при зіткненні з атомами ртуті передають атомам лише певні порції енергії, причому 4,86 еВ – найменша можлива порція енергії, яка може бути поглинена атомом ртуті в основному енергетичному стані, що експериментально підтверджує постулати Бора.

§. Опис стану частинки за допомогою квантових чисел. Спін. Дослід Штерна і Герлаха. Стан електрона в багатоелектронному атомі. Принцип Паулі. Періодична система елементів Менделєєва.

1⁰ У квантовій фізиці доводиться, що рівняння Шредінгера

(11.1)

задовольняють власні функції (), які визначаються трьома квантовими числами: головним n, орбітальним l i магнітним m_ℓ.

В виразі для власних значень енергії 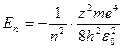головне квантове число n визначає енергетичні рівні електрона в атомі й може набувати будь-яких значень.

Таким чином, квантування енергії випливає з основних положень квантової механіки без будь-яких додаткових припущень.

2⁰ З розв’язання рівняння Шредінгера також випливає, що момент імпульсу електрона квантується

, (11.2)

де – орбітальне квантове число, яке при даному n набуває значення

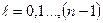, (11.3)

(тобто n - значень) i визначає момент імпульсу електрона в атомі.

3⁰ 3 розв’язання рівнянь Шредінгера випливає також, що вектор моменту імпульсу електрона може мати лише такі орієнтації у просторі, при яких його проекція 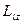на напрям z зовнішнього магнітного поля набирає квантованих значень, кратних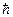

L_ℓz = ħm _ℓ, (11.4)

де 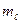– магнітне квантове число, яке при даному може набувати значення:

, (11.5)

тобто значень. Отже, магнітне квантове число m_ℓ визначає проекцію моменту імпульсу електрона на заданий напрям. Вектор моменту імпульсу електрона в атомі може мати в просторі орієнтацію, що повинно привести в магнітному полі до розчеплення рівня з головним квантовим числом n на підрівнів (явище П. Зеємана). Сумарна кількість можливих станів, які відповідають даному n, дорівнює:

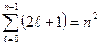. (11.6)

Отже, виходить, що заданому значенню п відповідає п ² різних хвилевих функцій. Іншими словами кажучи, повній енергії Е відповідає п ² різних хвилевих функцій. У подібних випадках говорять, що даний стан вироджений з кратністю звироднілості п ². Звироднілість знімається зовнішнім збудженням з боку електричного або магнітного поля.

4⁰ Оскільки при русі електрона в атомі істотні хвильові властивості електрона, то квантова механіка відмовляється від класичної уяви про електронні орбіти. Згідно з квантовою механікою, кожному енергетичному стану відповідає хвильова функція, квадрат модуля якої визначає ймовірність знаходження електрона в одиниці об’єму (яка в різних частинах атома різна). Електрон при своєму русі утворює електронну хмару, густина якої характеризується ймовірністю знаходження електрона в різних точках об’єму атома. Квантові числа n i характеризують розмір i форму електронної хмари, а квантове число 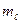характеризує орієнтацію електронної хмари в просторі.

В атомній фізиці стан електрона з 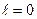називають s – станом, – р -станом, – d -станом, 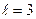– f- станом тощо. Наприклад, електрони в стані з , 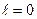і маркують відповідно символами 2 S i 2 P.

5⁰ Квантові числа n, i 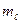дозволяють повніше описувати спектр випромінювання (поглинання) атома водню, ніж це зроблено в теорії Бора, завдяки правилам відбору. Теоретично доведено i експериментально підтверджено, що для дипольного випромінювання електрона, який рухається в центральносиметричному полі ядра, можуть відбуватися тільки такі переходи, для яких: 1) зміна орбітального квантового числа 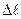задовольняє вимогам ; 2) зміна магнітного квантового числа задовольняє вимогам .

Враховуючи кількість можливих станів, що відповідають даному n, i правилу відбору, розглянемо спектральні лінії атома водню (рис. 11.1): серії Лаймана відповідають переходи (); серії Бальмера – , ; та ін.

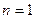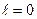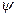6⁰ 1 s –стан (,,) в атомі водню є сферично-симетричним, тобто не залежить від кутів i . Хвильова функція електрона визначається в цьому стані тільки відстанню r електрона від ядра

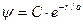, (11.7)

де перший боровський радіус для атома водню.

С – знайдемо з вимог нормування

Після інтегрування дістаємо 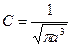і хвильову функцію

. (11.8)

Ймовірність знайти електрон в елементі об’єму дорівнює

Максимум виразу дістанемо при , тобто електрон може бути ймовірніше знайдено на відстані, що дорівнює боровському радіусу, хоча густина ймовірності відмінна від нуля i в останньому просторі.

Дата добавления: 2014-01-07