Множества и операции над ними

Под множеством понимается собрание определенных и различных между собой элементов, мыслимых как единое целое.

Множества будем обозначать заглавными русскими или латинскими буквами.

Если множество можно задавать некоторым свойством, по которому можно определить входит ли элемент в множество.

Свойство 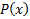задается предикатом. Если при подстановке конкретного элемента мы получаем истину, значит элемент принадлежит множеству, если ложь, значит не принадлежит.

(включает 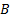), если для любого элемента из найдется равный ему из .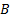

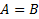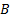(множество равно множеству ), если

Среди всех множеств особое значение имеют:

1. 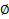(пустое множество) – множество не содержащие ни одного элемента

2. (универсальное множество) – множество, включающее в себя все рассматриваемые множества.

Например, если мы работаем только с целыми числами и множествами состоящими из целых чисел, то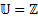

Придумать множество из 4-х элементов, элементами которого являются тоже множеством так, что для любых 2 элементов или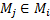

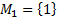
Понятие множества очень абстрактно.

В частности, можно рассмотреть множество всех существующих множеств и это не противоречит определению.

Существует множества являющееся элементами самих себя.

Это приводит к противоречиям, например:

Рассмотрим множества не являющиеся элементами самих себя. 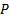– множество всех множеств не являющихся элементами самих себя. Является ли 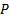элементом самого себя?

Пусть 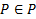, но по определению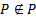

Пусть 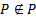, но по свойству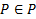

Дата добавления: 2014-01-07