
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бинарные отношения
|
|
|
|
Если  и
и 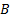 конечные множества, то прямое произведение
конечные множества, то прямое произведение 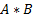 тоже конечно и содержит
тоже конечно и содержит 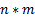 элементов, где
элементов, где 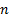 – количество элементов в множестве
– количество элементов в множестве  , а
, а 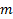 – в
– в 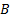 .
.
Пусть даны 2 множества  и
и 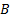 . Бинарным отношением между множествами
. Бинарным отношением между множествами  и
и 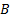 называется любое подмножество прямого произведения
называется любое подмножество прямого произведения 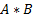 .
.
Если множества  и
и 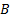 совпадают и мы рассматриваем прямое произведение
совпадают и мы рассматриваем прямое произведение 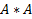 и берем бинарное отношение, то считается что это бинарное отношение задано на множестве
и берем бинарное отношение, то считается что это бинарное отношение задано на множестве  .
.
Пусть дано бинарное отношение 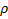 между множествами
между множествами  и
и 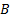 .
.
Областью определения называется  .
.
Областью значения называется 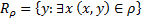 .
.
Пусть дано бинарное отношение 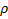 на множестве
на множестве  . Обратным к бинарному отношению называется отношение
. Обратным к бинарному отношению называется отношение 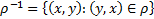 .
.
Пусть даны два отношения 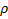 и
и  . Суперпозиций
. Суперпозиций 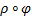 называется бинарное отношение, такое, что
называется бинарное отношение, такое, что 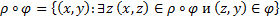 .
.
В общем случае 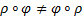
Среди всех бинарных отношений на  особую роль играют:
особую роль играют:
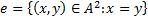 – тождественное бинарное отношение
– тождественное бинарное отношение
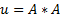 – универсальное бинарное отношение
– универсальное бинарное отношение
 на конечном множестве
на конечном множестве  можно построить граф этого бинарного отношения. Это схема, на которой все элементы множества
можно построить граф этого бинарного отношения. Это схема, на которой все элементы множества  изображаются точками на плоскости.
изображаются точками на плоскости.
Если для разных  и
и 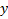
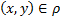 , то это изображается дугой со стрелкой от
, то это изображается дугой со стрелкой от  к
к 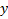 .
.
Если 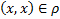 , то это изображается петлей вокруг
, то это изображается петлей вокруг  .
.
Свойства бинарных отношений:
1. Отношение 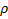 на множестве
на множестве  называется рефлексивным, если
называется рефлексивным, если 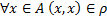
С точки зрения графа рефлексивность означает, что вокруг каждой точки графа есть дуга. Иначе не рефлексивно.
2. Отношение 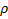 на множестве
на множестве  называется антирефлексивным, если
называется антирефлексивным, если 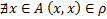
Антирефлексивность частный случай рефлексивности.
3. Отношение 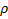 на множестве
на множестве  называется симметричным, если
называется симметричным, если 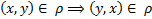
С т очки зрения графа симметричность означает, что все дуги двусторонние. Иначе не симметрично.
4. Отношение 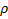 на множестве
на множестве  называется антисимметричным, если
называется антисимметричным, если
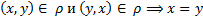
С точки зрения графа антисимметричность означает, что все дуги односторонние.
5. Отношение 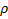 на множестве
на множестве  называется транзитивным, если
называется транзитивным, если
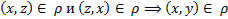
Иначе не транзитивное.
Замечание: если при анализе свойства нет ни одного примера нарушения свойства, значит свойство выполняется.
Определение: Отношение 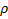 на множестве
на множестве  называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 581; Нарушение авторских прав?; Мы поможем в написании вашей работы!