Свойства бинарных отношений

Определение 1: Пусть на множестве задано отношение. Классом эквивалентности порожденным элементом называется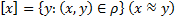

Каждый элемент может порождать свой класс эквивалентности.

Утверждение 1: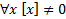

Доказательство: Так как отношение эквивалентности рефлексивно, то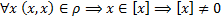

Утверждение 2: Если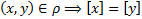

Доказательство6 Пусть 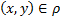, докажем, что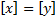

1)

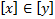
Пусть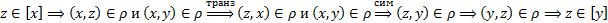

2) Аналогично

Определение 2: Предположим, что мы перебрали все множество и по каждому элементу построили класс эквивалентности, оставим только различные классы эквивалентности. Множество состоящее из этих различных классов называется фактор множества по отношению эквивалентности .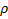

Обозначение: , т.е. только различные классы.

Если требуется определить фактор множества, то можно поступать следующим образом:

1. Берем любой элемент из

2. Строим класс порожденный этим элементом

3. Берем следующим элемент не попавший в первый класс

4. Строим по нему класс эквивалентности

5. Берем элемент ни первому, ни второму классу пока не исчерпается множество

Говорят, что классы эквивалентности образуют разбиение множества на подмножества.

Определение 3: Совокупность множеств :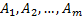

1.

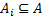
2.

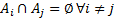
3.

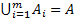
Образует разбиение множества на подмножества.

Замечание: Если мы имеем разбиение множества на подмножества, то по нему можно построить отношение эквивалентности, такое, что классы эквивалентности совпадут с подмножествами с подмножествами или фактор множества будет состоять из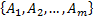

Данное отношение эквивалентности будет строиться следующим образом:

, при этом считается, что сам с самим собой принадлежит одному подмножеству.

Дата добавления: 2014-01-07