Геометрическое истолкование суммы, разности, произведения и частного двух комплексных чисел

Тригонометрическая форма записи комплексного числа

Из чертежа непосредственно видно , 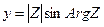. Отсюда следует, что 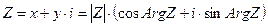(1) – тригонометрическая форма записи комплексного числа.

Пусть нам даны два комплексных числа с₁ = а₁ + b₁·i и с₂ = а₂ + b₂·i. Составим их сумму с = с₁ + с₂ = (а₁ + а₂) + i · (b₁ + b₂). Изобразим с₁ и с₂ векторами с началом в нуле. Построим на них параллелограмм.

Очевидно сумма с=с₁+с₂ изображается вектором диагонали параллелограмма, построенного на векторах с₁ и с₂ с началами в нуле. Т. е. сумму можно находить по правилу сложения векторов.

Из чертежа непосредственно следует, что 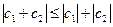(2) – это неравенство распространяется на любое число слагаемых.

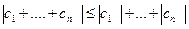
Рассмотрим теперь разность с = с₁-с₂, где с₁ = а₁+b₁·i и с₂ = а₂+b₂·i. Очевидно с = (а₁-а₂)+i·(b₁-b₂) или с = с₁+(-с₂).

Нетрудно видеть, что вектор (-с₂) получается из вектора с₂ изменением направления на противоположное. Вектор с = с₁-с₂ получается в результате сложения вектора с₁ и (-с₂). Таким образом число с = с₁-с₂ изображается вектором, соединяющим точки с₁ и с₂, причем начало его помещено в точке с₂, а конец в точке с₁. Модуль разности с₁-с₂ есть расстояние между точками с₁ и с₂.

Из чертежа непосредственно видно, что 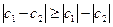, можно показать, что ;

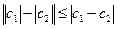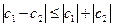
Равенство имеет место только в том случае, когда эти векторы коллинеарные.

Возьмем два произвольных комплексных числа: 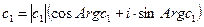, 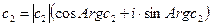и составим их произведение с = с₁·с₂ = |с₁|·|c₂|· [ (сosArg с₁ · сosArg с₂ - sinArg с₁ · sinArg с₂)+i·(sinArg с₁ · сosArg с₂ + сosArg с₁ · sinArg с₂) ] = |с₁|·|c₂|· [ cos(Arg с₁ + Arg с₂) + i·sin(Arg с₁ + Arg с₂) ]. Следовательно |c| = |с₁|·|c₂| =|с₁·c₂|, Arg c = Arg(с₁·с₂) = Arg с₁+Arg с₂ (сумма аргументов – алгебраическая сумма). Отметим, что Arg c² = Arg c + Arg c и не равно 2·Arg c. Но можно Arg c² = 2·arg c + 2кπ. Таким образом комплексное число с = с₁·с₂ изображается вектором, который получается из вектора с₁ путем его растяжения в |c₂| раз и путем поворота полученного вектора на угол Arg с₂.

Легко устанавливается, что модуль произведения любого конечного числа чисел равен произведению их модулей 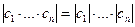и аргумент произведения равен сумме аргументов сомножителей Arc(c₁·…·c_n)=Argс₁+…+Argc_n. В частности есть с₁ = с₂ = … = с_n, то 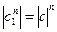, Arg сⁿ=Arg c+…+Arg с = n·arg с+2кπ (k = 0, 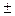1, 2, …). Таким образом

cⁿ = |c|ⁿ·(сos nArg с+ i·sin nArg с), n ≥ 2 (3)

Полученная формула называется формулой Муавра. Часто формулой Муавра называют другую формулу (cosφ+i·sinφ)ⁿ = cos nφ+ i·sin nφ (4)

Рассмотрим два комплексных числа с₁ и с₂, с₂ ≠ 0. 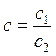. По определению частного с₁ = с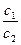·с₂ = ·с₂.

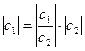
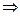
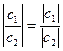
Arg c₁ = Arg 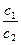+ Arg c₂

Arg 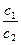= Arg c₁ - Arg c₂

Итак, с =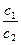= 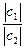[ cos(Arg c₁ - Arg c₂)+i·sin(Arg c₁ - Arg c₂) ]

Комплексное число с = 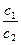изображается вектором, который получается из вектора с₁ путем его сжатия в 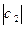раз, затем поворотом полученного вектора на угол (-Arg c₂)

6. Корень n – ой степени из комплексного числа

Возьмем произвольное комплексное число с и натуральное число n 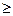2.

Комплексное число Z называется корнем n–ой степени из комплексного числа c, если Zⁿ = c.

Найдем все значения корня n– ой степени из комплексного числа с. Пусть c=|c|·(cos Arg c+i·sin Arg с), а Z = |Z|·(сos Arg Z + i·sin Arg Z), где Z корень n- ой степени из комплексного числа с. Тогда должно быть 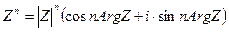= c = |c|·(cos Arg c+i·sin Arg с). Отсюда следует, что 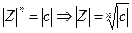и n·Arg Z = Arg с 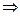Arg Z = 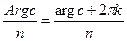(k=0,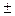1,…). Следовательно, Z = 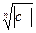(cos 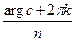+ i·sin 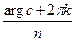), (k=0,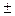1,…). Легко увидеть, что любое из значений 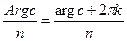, (k=0,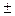1,…) отличается от одного из соответствующих значений 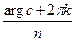,(k = 0,1,…,n-1) на кратное 2π. Поэтому

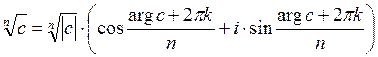, (k = 0,1,…,n-1).

Дата добавления: 2014-01-07