Непрерывные случайные величины

1) 1; 2) 2; 3) 4; 4) 8.

Биномиальное; 2) Пуассона; 3) Паскаля; 4) гипергеометрическое.

Тесты

1) 3,3; 2) 0,3; 3) 0; 4) 0,5.

47.

Математическое ожидание; 2) cреднее квадратическое отклонение; 3) начальный момент второго порядка; 4) центральный момент первого порядка.

Математическое ожидание; 2) дисперсия; 3) среднее квадратическое отклонение; 4) центральный момент первого порядка.

Тесты

Минус бесконечности; 2) нулю; 3) единице; 4) бесконечности.

Тесты

41. Чему равно значение функции распределения случайной величины на минус бесконечности?

42. По какой формуле можно вычислить вероятность попадания значения случайной величины с функцией распределения F (x) на интервал (a, b)?

1) F (b - a); 2) F (a) + F (b); 3) F (a) - F (b); 4) F (b) - F (a).

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Математическое ожидание

Математическим ожиданием (средним значением или арифметическим средним) дискретной случайной величины называется сумма произведений всех её возможных значений на их вероятности:

М (Х) = .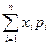

В приведённом выше примере М (Х) = 0 × 0,06 + 1 × 0,38 + 2 × 0,56 = 1,5.

Свойства математического ожидания. 1) М (С) = С. 2) М (С Х) = С × М (Х). 3) М (Х ± Y) = М (Х) ± М (Y). 4) Если Х и Y – независимые случайные величины, то М (Х × Y) = М (Х) × М (Y).

Дисперсия

Дисперсией (рассеянием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

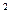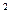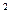D (Х) = М {[X – М (Х)]} = М (Х ) - М (Х).

В нашем примере D (Х) = (0 – 1,5)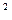× 0,06 + (1 – 1,5)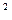× 0,38 + (2 – 1,5)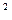× 0,56 = 0,37.

Среднее квадратическое отклонение

Средним квадратическим отклонением случайной величины называется квадратный корень из дисперсии:

s(Х) = .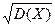

В нашем случае s = 0,61.

Начальный момент

Начальным моментом порядка k случайной величины Х называется математическое ожидание величины :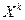

.

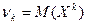Центральный момент

Центральным моментом порядка k случайной величины Х называется математическое ожидание величины :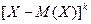

.

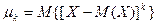43. Пусть C - неслучайная, а X - случайная величина. Чему равна дисперсия D (C × Х)?

1) D (Х); 2) С × D (Х); 3) C ² × D (Х); 4) 0.

44. Как называется среднее значение случайной величины, около которого группируются возможные значения случайной величины?

45. Пусть C - неслучайная, а X - случайная величина. Чему равно математическое ожидание M (C × X)?

1) 0; 2) M (Х); 3) С × M (Х); 4) Х × M (С).

46. Как называется число, равное квадратному корню из дисперсии случайной величины?

Лекция 5

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Приведём здесь шесть наиболее распространенных законов распределения.

Распределение Бернулли (биномиальное)

Вероятности случайной величины Х = k вычисляются по формуле Бернулли (3):

.

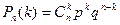Математическое ожидание и дисперсия для этого распределения равны соответственно М (Х) = np, D (Х) = npq.

П р и м е р. Пусть случайная величина Х = k – это число выпавших орлов при n = 3 подбрасываниях монеты. Вероятности выпадения p и невыпадения q орла одинаковы и равны 0,5. Величина Х может принимать четыре значения: 0, 1, 2, 3. Соответствующие вероятности, вычисленные по формуле (3), равны 0,125; 0,375; 0,375; 0,125. Математическое ожидание равно 3 × 0,5 = 1,5, дисперсия – 3 × 0,5 × 0,5 = 0,75, а среднее квадратическое отклонение - 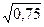= 0,87.

Распределение Пуассона

Вероятности случайной величины Х = k вычисляются по формуле Пуассона (6):

.

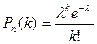Математическое ожидание и дисперсия для этого распределения совпадают и равны параметру распределения: М (Х) = D (Х) = l = np.

П р и м е р. Ёлочная гирлянда содержит 1000 электроламп, вероятность выхода из строя которых в течение новогодних праздников равна 0,01, т.е. параметр l = 1000 × 0,01 = 10. За этот период могут перегореть от нуля до тысячи ламп: Х = k = 0 ¸1000 ламп. Вероятности, вычисленные по формуле (6), равны Р (0)» 4,54 ×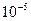, Р (1)» 4,54 ×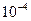, Р (2)» 2,27 ×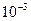,…, Р (10)» 0,125,…, Р (20)» 1,87 ×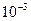,…. Математическое ожидание и дисперсия равны 10, среднее квадратическое отклонение – 3,16.

Геометрическое распределение

Вероятности случайной величины Х вычисляются по формуле Р (Х = k) = 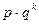. Математическое ожидание и дисперсия для этого распределения равны

соответственно М (Х) = q / p и D (Х) = .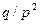

Геометрическое распределение появляется в биномиальной схеме, когда число испытаний не ограничено, а случайная величина Х – это количество испытаний до первого успеха.

П р и м е р. Имеется связка из 10 однородных ключей, из которых только один открывает дверь. Вы подбираете в темноте ключ, не откладывая уже использованный (ситуация редкая, но допустимая). Понятно, что чисто теоретически дверь можно открывать очень и очень долго. Вероятность p успеха в данном примере равна 0,1, а неудачи q – 0,9. Вероятности случайных величин Х будут равны: Р (0) = 0,1; Р (1) = 0,1 × 0,9 = 0,09; Р (2) = 0,1 × 0,9 × 0,9 = 0,081 и т.д. Среднее число безуспешных попыток открыть дверь равно 0,9 / 0,1 = 9, а их среднее квадратичное отклонение - .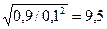

Распределение Паскаля

Вероятности случайной величины Х вычисляются по формуле

Р (Х = k) = 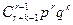. (7)

Математическое ожидание и дисперсия для этого распределения равны соответственно М (Х) = r× q / p и D (Х) = r× .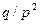

Здесь, также как и в предыдущем случае, число испытаний не ограничено, но случайная величина Х = k – это общее число неудач, предшествующих наступлению r- го очередного успеха.

З а д а ч а. Предположим, что Вы попадаете в мишень с вероятностью p = 0,4. Сколько Вы совершите промахов до тех пор, пока не попадете в мишень, например, k = 10 раз?

Решение. Аналогично предыдущему случаю, теоретически до 10-го попадания стрелять можно до бесконечности. Случай Х = 0 соответствует ситуации, когда все 10 выстрелов были удачными, а значит, Р (0) = 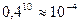. Расчеты по формуле (7) дают такие результаты: Р (1) =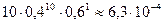; Р (2)» 2,1× 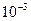и т.д. Среднее число промахов составит 10 × 0,6 / 0,4 = 15, а среднее квадратическое отклонение будет равно .

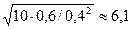Гипергеометрическое распределение

Вероятности случайной величины Х вычисляются по формуле

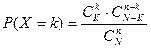, (8)

где числа N, K, n являются параметрами распределения.

Математическое ожидание и дисперсия для этого распределения равны соответственно М (Х) = 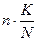и D (Х) = .

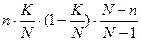При n >> 1 гипергеометрическое распределение приближается к биномиальному.

Такое распределение встречается в задаче о выборке без возврата n элементов из N элементов, из которых определённым свойством обладают K элементов. При этом нас интересует, сколько элементов k из выбранных n обладают отмеченным свойством. Предполагается, что n 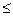K.

П р и м е р. К экзамену надо выучить N = 100 вопросов, но Вам удалось подготовить только K = 80. На экзамене Вы получаете n = 4 вопроса. Из них выученными (k) могут оказаться 4 вопроса (это “отл”), 3 – (“хор“), 2 – (“уд”), 1 или 0 – (“неуд”). Распределение случайной величины Х = k гипергеометрическое. Соответствующие вероятности, рассчитанные по формуле (8), равны:

Р (0) =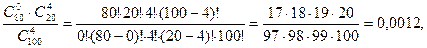

Р (1) =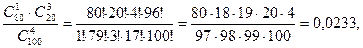

Р (2) = 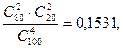Р (3) = 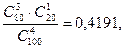Р(4) =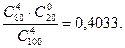

Как видим, при такой подготовке к экзамену вероятность получить ”хор” будет наибольшей и чуть выше, чем заслужить “отл”. Среднее число доставшихся выученных вопросов равно М (Х) = 4×80/100 = 3,2, дисперсия – D (Х) = 1,86, а среднее квадратическое отклонение – s = 1,36.

Равномерное распределение

Для этого распределения вероятности всех n значений случайной величины одинаковы и равны Р (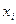) = 1 / n.

П р и м е р. В примере для геометрического распределения ключ из связки из 10 однородных ключей после неудачной попытки открыть им дверь не удалялся. Гораздо естественнее допустить, что он изымается из связки в дальнейших экспериментах. Пусть в этом случае случайная величина Х – это число использованных ключей, а через 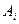обозначим событие: дверь открылась с i -ой попытки. Тогда Р (Х = 1) = Р (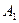) = 1/10. Остальные вероятности получить тоже несложно: Р (Х = 2) = Р (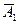×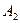) = Р (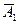) × Р (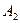) = = 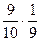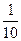, Р (Х = 3) = Р (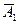××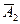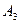) = Р (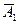) × Р (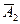) × Р (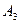) = 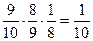, …. И мы видим, что распределение получается равномерным: вероятности всех 10 случайных величин (1,2,…,10) одинаковы и равны 1/10.

Математическое ожидание совпадает со средним арифметическим: М (Х) = (1 + 2 +…+ 10) / 10 = 5,5, дисперсия D (Х) = 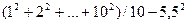= 8,25, а среднее квадратическое отклонение s = 2,87.

Нестандартные распределения

Однако на практике чаще встречаются с нестандартными распределениями. В этом случае отыскивают вероятность каждого из значений случайной величины.

З а д а ч а. На первом этаже четырёхэтажного дома в лифт входят 5 человек.

Каждый пассажир независимо от других с одинаковой вероятностью может выйти на любом этаже, начиная со второго. Случайной величиной Х будем считать номер этажа, на котором лифт сделал первую остановку. Найти закон распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.

Решение. Вероятность выйти любому пассажиру на любом из трёх этажей (2, 3, 4) равна р = 1/3, вероятность невыхода - q = 2/3. Событием 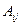назовём выход i -го пассажира на j -ом этаже. Случайная величина Х может принимать три значения: 2, 3, 4.

Лифт сделает первую остановку на втором этаже (событие 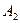), если на нём выйдет хотя бы один пассажир. Это событие 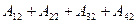. Вероятность такого события рассчитаем по формуле (2) “вероятности хотя бы одного события”:

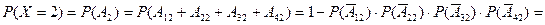
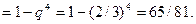
Лифт сделает первую остановку на третьем этаже (событие 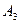), если никто не выйдет на втором (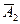), а на третьем выйдет хотя бы один человек. Это событие 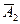× 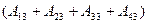. Вероятность такого события равна

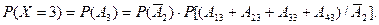
Рассмотрим условную вероятность 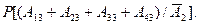Здесь сумма событий 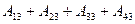должна произойти при условии, что на втором этаже никто не вышел, т.е. осталось только два этажа для выхода пассажиров. В этом случае вероятность выйти равна уже не 1/3, а 1/2 и совпадает с вероятностью невыхода. Тогда условная вероятность

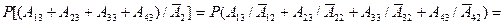
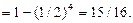
Поэтому вероятность Р (Х = 3) численно равна

Р (Х = 3) = (1 – 65/81) × 15/16 = 15/81.

Лифт сделает первую остановку на четвёртом этаже (событие 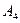), если никто не вышел на втором (событие 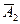=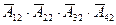) и третьем этажах (событие 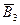= 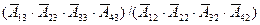). При таком стечении обстоятельств вероятность выхода любого пассажира на четвёртом этаже будет уже равна единице (выше ехать некуда). Вероятность такого сложного события

будет равна

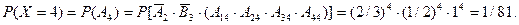
Впрочем, последнюю вероятность можно было посчитать и гораздо проще: ведь это вероятность всем четырём пассажирам выйти на одном этаже, т.е. .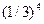

Как и полагается, сумма всех трёх вероятностей равна 1: Р (Х = 2) + Р (Х = 3) + Р (Х = 4) = 1 (это рекомендуется обязательно проверить).

Закон распределения случайной величины Х запишем в таблицу

Х
р	65/81	15/81	1/81

Математическое ожидание равно М (Х) = (130 + 30 +4) / 81 = 2,0247. Дисперсия равна D (Х) = (4 × 65 + 9 × 15 + 16 × 1) / 81 - 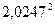= 0,9747. Среднее квадратическое отклонение равно s = 0,99.

48. Какое распределение случайных величин в теории вероятностей справедливо для редких событий?

49. Монету подбрасывают 3 раза. Найти дисперсию случайной величины Х – числа выпадений герба.

1) 1/4; 2) 2/3; 3) 3/8; 4) 3/4.

50. Имея неограниченное количество патронов, сколько в среднем Вы сделаете выстрелов для поражения цели при вероятности попадания в неё 0,2?

Лекция 6

Функция распределения непрерывной случайной величины Х определяется также, как и для дискретной: F(x) = Р (Х < x). И случайная величина называется непрерывной, если её функция распределения является непрерывной функцией с кусочно-непрерывной производной. Кроме функции распределения, которую называют ещё интегральной, для непрерывной случайной величины вводят дифференциальную функцию распределения, которую называют также плотностью распределения вероятностей, или плотностью вероятностей, или плотностью распределения: p(x) = .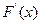

Свойства плотности распределения

1) Плотность распределения и функция распределения связаны между собой соотношениями: p(x) = 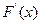и 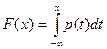. 2) p(x) ³ 0.

3)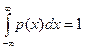. 4) Р (a < X < b) = 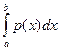. 5) Р (Х = a) = 0.

Последнее свойство говорит о невозможности непрерывной случайной величине принять одно конкретное значение.

Вероятностный смысл плотности распределения

Вероятность того, что случайная величина примет значение, принадлежащее интервалу (x, x+Dx), приближенно равна произведению плотности распределения в т. x на длину интервала: Р (x < Х < x + Dx)» p (x) × Dx.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Математическое ожидание: М (Х) =.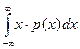

Дисперсия: D (Х) =.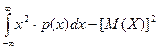

Среднее квадратическое отклонение: s(Х) = .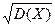

З а д а ч а. Задана плотность распределения р(х): .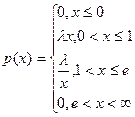

Найти l, М (Х), D (Х), s, Р (0,5 £ Х £ 2).

Решение. Параметр l найдем, используя свойство 3) плотности распределения: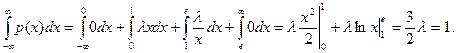

Отсюда l = 2/3.

Математическое ожидание равно М (Х) =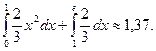

Дисперсия равна D (X) = .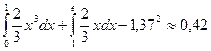

Среднее квадратическое отклонение s»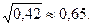

Вероятность попадания случайной величины Х в интервал (0,5; 2) равна Р (0,5 £ Х £ 2) =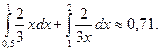

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Приведём пять наиболее распространённых законов распределения непрерывных случайных величин.

Равномерное распределение

Плотность распределения и функция распределения вычисляются по формулам

, .

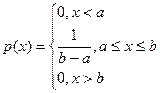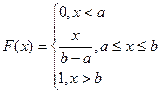Математическое ожидание и дисперсия соответственно равны: М (Х) = 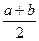, D (X) = .

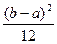П р и м е р. Равномерному распределению подчиняется время ожидания поезда метро при условии, что интервал движения поездов постоянен, а пассажир приходит на станцию каждый раз в не планируемый заранее момент времени. Если интервал движения равен 3 мин., то среднее время ожидания поезда составляет 1,5 мин., а среднее квадратическое отклонение - 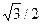мин. = 52 сек.

Показательное (экспоненциальное) распределение

Плотность распределения и функция распределения в этом случае равны

, .

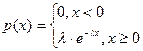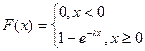Математическое ожидание и дисперсия находятся по формулам:

М (Х) = 1/ l, D (X) = 1/.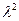

Показательное распределение хорошо описывает время службы приборов и время обслуживания клиентов.

З а д а ч а. Пусть заявленное заводом среднее время службы телевизора равно 20 годам; это означает, что параметр распределения равен l = 1/20. Найти вероятность выхода из строя телевизора в течение одного года при условии, что до этого он безотказно проработал время Т.

Решение. Искомую вероятность для Dt = 1 вычислим, используя формулу (1) для условной вероятности:

.

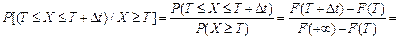
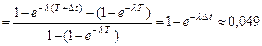Как видим, результат не зависит от уже отработанного времени Т, т.е. если телевизор не вышел из строя за какой-то срок, то в течение следующего года вероятность сломаться у него одна и та же. Естественно, так будет в случае выполнения показательного закона распределения для времени нормальной работы прибора. Такое свойство этого распределения называют “ отсутствием последействия ”, и вводят понятие функции надёжности (вероятность безотказной работы за время Т): R (T) = Р (X > T) = 1 – Р (X < T) = 1 – F (T) = 1 – [1 – exp (- lT)] = = exp (- lT). Величину l называют интенсивностью отказов.

Нормальное (гауссово) распределение

Самое распространённое распределение непрерывной случайной величины описывается формулой:

.

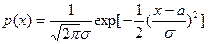Здесь через a обозначено математическое ожидание, а через s - среднее квадратическое отклонение.

Нормированным нормальным распределением называется распределение, у которого a = 0 и s =1.

Вероятность случайной величине оказаться в интервале (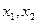) равна

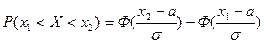, (9)

где Ф (х) – интеграл вероятности.

Вероятность отклонения на величину d от математического ожидания a получается из формулы (9), если положить в ней 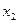= а + d, а 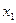= а - d:

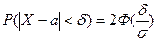. (10)

Если в последней формуле взять d = 3 s, то получим 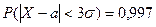, т.е. вероятность практически равную 1. Это означает, что нормально распределённая случайная величина отклоняется от своего математического ожидания на величину, большую, чем 3 s, с вероятностью всего 0,3%. Это обстоятельство называют “ правилом трёх сигм ”. Для любых других распределений установлено, что 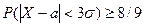(см. ниже Неравенство Чебышёва).

З а д а ч а. Вы регулярно покупаете половину килограммовой буханки черного хлеба, и очевидно, что средний вес а за большой промежуток времени составит 500 г. Предположим, что продавец при разрезании буханки ошибается в среднем на 30 г, и эту величину можно принять за среднее квадратическое отклонение s. Определить вероятность того, что Вы получили из рук продавца полбуханки, вес которой заключен между 480 и 520 г.

Решение. Для нахождения вероятности Р (480 < X < 520) воспользуемся формулой (10), которая дает следующее значение: 2 Ф (20 / 30)» 0.5.

Логарифмически-нормальное (логнормальное) распределение

В этом случае по нормальному закону распределен логарифм случайной величины Х:

.

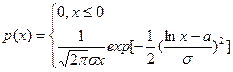Здесь а и s - это математическое ожидание и среднее квадратическое отклонение ln Х.

По такому закону, например, распределен размер дохода, который зависит от многих случайных факторов и который пропорционален уже достигнутому уровню накопления. Ему же подчинены размеры частиц при дроблении (например, помол кофейных зёрен в кофемолке).

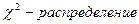с n – свободы

Если 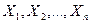- попарно независимые нормальные случайные величины, то случайная величина 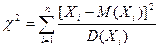имеет 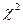- распределение с n -степенями свободы.

П р и м е р. Есть n покупателей половинок черного хлеба, не стоящих с очереди друг за другом (иначе случайные величины 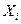окажутся зависимыми). Все они определяют вес 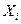своего хлеба, складывают разности 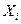- 500, возведённые в квадрат, и делят получившуюся сумму на 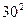(конкретные цифры взяты из задачи для нормального распределения). Найденная случайная величина будет иметь 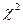- распределение.

Дата добавления: 2014-01-07