Закон больших чисел

В общем виде законом больших чисел называют формулировку условий, при которых совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

Центральная предельная теорема (теорема Ляпунова)

Если случайная величина Х является суммой большого числа взаимно независимых величин, так что влияние каждой из них на общую сумму незначительно, то Х имеет распределение, близкое к нормальному.

Поскольку на практике очень часто приходится сталкиваться именно с подобной ситуацией, то понятно, почему это распределение такое распространённое.

Неравенство Маркова

Вероятность положительной случайной величине X принять значение меньшее e удовлетворяет неравенству

.

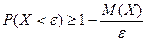З а д а ч а. Оценить число вкладчиков банка, если известно, что общая сум- ма вкладов составляет 600 000 рублей, а вероятность того, что произвольно взятый вклад меньше 1000 рублей, равна 0,6.

Решение. Обозначим число вкладчиков банка через N. Тогда средний вклад будет равен М (X) = 600 000 / N. В соответствии с равенством Маркова

0,6 = Р (Х<1000) ³ 1 - 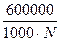. Решая это неравенство относительно неизвест­ного числа вкладчиков, найдем оценку: N £ 1500.

Неравенство Чебышёва

Вероятность отклонения случайной величины X от её математического ожидания на величину меньшую e удовлетворяет неравенству

.

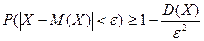Если считать, что e = 3 s, то предыдущее неравенство запишется как “ правило трёх сигм ” для любого распределения: .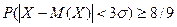

З а д а ч а. В заряде для залпа праздничного салюта 200 мелких зарядов. Вероятность того, что любой из них зажжётся в небе, равна 0,95. Оценить вероятность отклонения числа вспыхнувших в небе огней от своего математического ожидания не более, чем на 5.

Решение. Прежде всего, надо найти среднее число разорвавшихся зарядов и их дисперсию. Так как это схема биномиальная (взрыв – осечка), то М (X) = np = 200 × 0,95 = 190, а D (X) = npq = 190 × 0,05 = 9,5. По неравенству Чебышёва оцениваем интересующую нас вероятность:

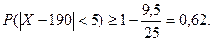
Теорема Чебышёва (закон больших чисел)

Если 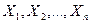- попарно независимые случайные величины с ограниченными дисперсиями, то их среднее арифметическое с большой вероятностью будет как угодно мало отличаться от среднего арифметического их математических ожиданий, если n стремиться к бесконечности.

Математически эта теорема записывается в следующем виде: каково бы ни было e > 0,

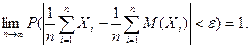
Закон больших чисел при различных предположениях доказывали Марков (эту теорему называют и его именем), Колмогоров, Хинчин.

Теорема Бернулли

Если в n независимых испытаниях вероятность появления события А одинакова и равна р, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет как угодно малым, если число испытаний достаточно велико: для любого e

.

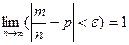Смысл последней теоремы заключается в том, что при большом числе испытаний статистическое определение вероятности практически совпадает с классической оценкой вероятности, осуществляемой умозрительно, без каких-либо экспериментов (см. в начале этого пособия про опыты Бюффона и Пирсона).

Дата добавления: 2014-01-07