Л И Т Е Р А Т У Р А. Логарифмически-нормальному; 2) равномерному; 3) показательному; 4) нормальному

Ответы

Логарифмически-нормальному; 2) равномерному; 3) показательному; 4) нормальному.

Тесты

58. Какой теореме соответствует утверждение: «при большом числе независимых опытов среднее арифметическое измеренных значений случайной величины приближается к её математическому ожиданию»?

1) теореме Ляпунова; 2) теореме Чебышёва; 3) теореме Пуассона; 4) теореме Бернулли.

59. Какой теореме соответствует утверждение: «при суммировании большого числа случайных величин закон распределения суммы при определённых условиях приближается к нормальному»?

1) центральной предельной теореме; 2) теореме Чебышёва; 3) теореме Пуассона.

60. Какому закону, скорее всего, подчиняется случайная величина: число вызовов, поступивших на телефонную станцию за сутки?

Приложение

Таблица значений функции Лапласа 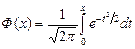(приведены только знаки после запятой).

х
0,0	0,0000	0,0040
0,1	0,0398
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1										38 30
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9					47 38
2,0				47SS
2,1
2,2
2,3
2,4	49 I8
2,5
2,6
2,7
2,8
2,9

х		х		х		х
3.0	0,49865	3,5	0,49977	4,0	0,499968	4,5	0,4999966
3.1	0,49903	3,6	0,49984	4,1	0,499979	4,6	0,4999979
3.2	0,49931	3,7	0,49989	4,2	0,499987	4,7	0,4999987
3.3	0,49952	3,8	0,49993	4,3	0,499991	4,8	0,4999992
3,4	0,49966	3,9	0,49995	4,4	0,499995	4,9	0,4999995

1) 3; 2) 1; 3) 4; 4) 4; 5) 2; 6) 4; 7) 2; 8) 3; 9) 4; 10) 3; 11) 3; 12) 4; 13) 2; 14) 3; 15) 3; 16) 2; 17) 2; 18) 4; 19) 1; 20) 3; 21) 2; 22) 1; 23) 2; 24) 1; 25) 4; 26) 2; 27) 1; 28) 4; 29) 3; 30) 1; 31) 4; 32) 2; 33) 3; 34) 2; 35) 2; 36) 3; 37) 4; 38) 4; 39) 2; 40) 2; 41) 2; 42) 4; 43) 3; 44) 1; 45) 3; 46) 2; 47) 1; 48) 2; 49) 4; 50) 3; 51) 1; 52) 1; 53) 2; 54) 3; 55) 2; 56) 1; 57) 3; 58)2; 59) 1; 60) 4.

1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для втузов. – М., 1977.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления. Для втузов. Т. 2. – М., любой год изд.

3. Мацкевич И. П., Свирид Г.П. Высшая математика. Теория вероятностей и математическая статистика. – Минск, 1993.

4. Чистяков В.П. Курс теории вероятностей. - М.: Наука, 1987.

5. Данко Н.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т.1. - М.: Высшая школа, 1980.

Дата добавления: 2014-01-07