Вектор ускорения точки

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.

Пусть в некоторый момент времени 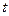движущаяся точка находится в положении 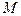и имеет скорость 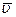, а в момент 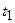приходит в положение 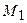и имеет скорость 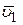(Рис. 48).

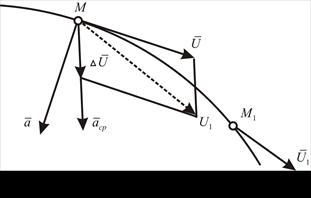
Рис. 48. К определению ускорения точки.

Тогда за промежуток времени 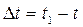скорость точки получает приращение 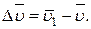Вычтем из вектора 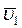скорость 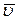и получим разность 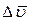(Рис. 48). Заметим, что вектор 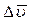направлен в сторону вогнутости кривой (траектории).

Отношением приращения вектора скорости 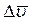к соответствующему промежутку времени 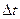определяет вектор среднего ускорения точки за этот промежуток времени:

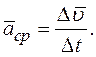(5)

Вектор среднего ускорения имеет то же направление, что и вектор 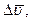т.е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени 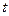называется векторная величина 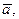к которой стремится среднее ускорение 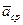при стремлении промежутка времени 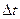к нулю:

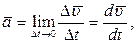
или, с учетом равенства (4):

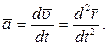(6)

Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.

Размерность ускорения .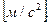

При прямолинейном движении вектор 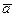направлен вдоль прямой, по которой движется точка.

5.4. Естественный способ задания движения.

Пусть задана траектория движения точки. Тогда положение точки 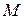на траектории будет однозначно определено криволинейной координатой 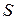(Рис. 49).

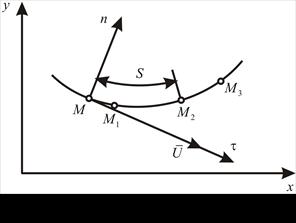
Рис. 49. Траектория точки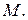

Чтобы знать положение точки на траектории в любой момент времени, достаточно знать закон

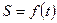. (7)

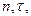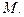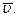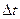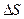Введём подвижные оси связанные с точкой Найдём значение Если за промежуток времени точка совершит вдоль дуги траектории перемещение где одновременно – приращение координаты 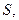то численно средней скоростью точки за этот промежуток времени будет

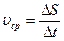
и в пределе

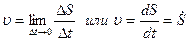. (8)

Т.е. числовое значение скорости точки в данный момент времени равно первой производной от расстояния (криволинейной координаты) 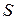этой точки по времени.

Дата добавления: 2014-01-07