Касательное и нормальное ускорения точки

ТВЕРДОГО ТЕЛА

ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ

ЛЕКЦИЯ № 6

Запишем ещё раз выражение (6):

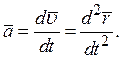(9)

Введём на Рис. 48 оси и 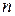,спроектируем вектор 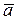(9) на эти оси.

Тогда:

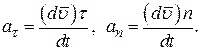(10)

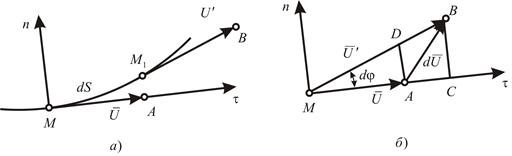
Рис. 50. К определению нормальной и касательной составляющих ускорения.

Вектор представляет собой разность между скоростями в двух соседних точках М и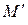(Рис. 50, а), т.е. 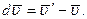Отложим векторы 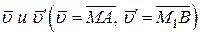от общего начала (Рис. 50,б) тогда 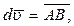и фигуру 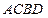при бесконечно малом угле можно рассматривать как прямоугольник. Отсюда

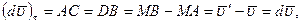
где 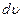– элементарное приращение числового значения скорости.

Далее, поскольку предел отношения дуги к хорде равен единице, можно 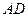рассматривать как элементарную дугу радиуса 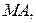размер которой определяется произведением радиуса на центральный угол. Тогда

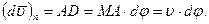
Подставляя найденные значения 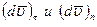в равенства (10), получим:

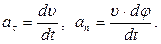(11)

Напомним, что отношение 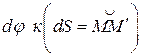(Рис. 50, а) определяет

кривизну кривой в точке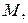а кривизна 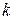является величиной, обратной радиусу кривизны 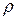в этой точке, т.е.

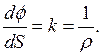(12)

Введём (12) во второе равенство из (11) и преобразуем его, учтя выражение (8), к виду

.

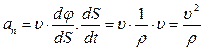В результате получим:

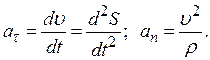(13)

Эти выражения – одна из важнейших теорем кинематики. Величины 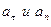называются касательным и нормальным ускорениями точки.

6.2. Поступательное движение твёрдого тела.

Поступательным называется такое движение твёрдого тела, при котором любая прямая, проведённая в этом теле, перемещается, оставаясь параллельной своему начальному направлению.

Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.

Пусть (Рис. 51) твёрдое тело совершает поступательное движение в системе 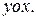Две произвольные точк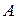и и 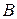в момент времени 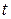определяются в этой системе двумя радиусами-векторам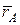и и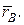

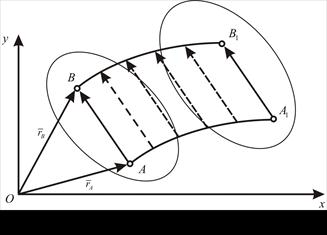
Рис. 51. Поступательное движение твердого тела.

Соединим 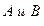вектором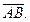

Тогда: 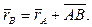(14)

Из Рис. 51 видно, что вектор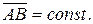

Продифференцируем обе части равенства (14) по времени:

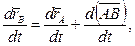
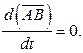
Причем

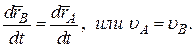(15)

Возьмём от обеих частей (15) производные по времени:

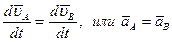(16)

Из (15) и (16) можно сделать вывод, что скорости и ускорения точек тела в любой момент времени одинаковы по модулю и направлению. Теорема доказана.

Дата добавления: 2014-01-07