Интерференция волн

Интерференция - это перераспределение потока электромагнитной энергии в пространстве, возникающее в результате наложения волн, приходящих в данную область пространства от разных источников. Если в области интерференции световых волн поставить экран, то на нем будут

наблюдаться светлые и темные области, например полосы.

Интерферировать могут только когерентные волны. Источники(волны) называют когерентными, если они имеют одинаковую частоту w и постоянную во времени разность фаз, излучаемых ими волн.

Когерентными могут быть только точечные монохроматические источники. К ним по свойствам близки лазеры. Обычные источники излучения некогерентны, так как немонохроматичны и не являются точечными.

Немонохроматичность излучения обычных источников обусловлена тем, что их излучение создается атомами, испускающими в течение времени порядка t=10^-8 с волновые цуги длиной L=ct =3м. Излучения разных атомов не коррелированы друг с другом.

Однако наблюдать интерференцию волн можно и при использовании обычных источников, если с помощью какого-либо приема создать два или более источников, подобных первичному источнику. Существует два метода получения когерентных световых пучков или волн: метод деления волнового фронта и метод деления амплитуды волны. В методе деления волнового фронта пучок или волна делится, проходя через близко расположенные щели или отверстия (дифракционная решетка), либо с помощью отражающих и преломляющих препятствий (бизеркало и бипризма Френеля, отражательная дифракционная решетка).

В методе деления амплитуда волны излучение делится на одной или нескольких частично отражающих, частично пропускающих поверхностях. Примером является интерференция лучей, отраженных от тонкой пленки.

Точки А, В и С на рис. являются точками деления амплитуды волны

Количественное описание интерференции волн.

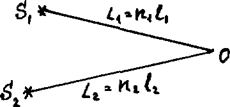
Пусть две волны, приходят в точку О от источников S₁ и S₂ по разным опти­ческим путям L₁=n₁l₁ и L₂=n₂l₂.

Напряженность результирующего поля в точке наблюдения равна

`E=`E₁+`E₂. (1)

Детектор излучения(глаз) регистрирует не амплитуду, а интенсивность волны, поэтому возведем соотношение (1) в квадрат и перейдем к интенсивностям волн

E²=E₁²+E₂²+2`E<sub>1</sub>`E₂ (2)

Усредним это выражение по времени

<E²>=<E₁²>+<E₂²>+2<`E<sub>1</sub>`E₂> (2)

Последнее слагаемое в (3) 2<E₁E₂> называют интерференционным членом. Его можно записать в виде

2<`E<sub>1</sub>`E₂>=2<E₁E₂cosd> (4)

где d - угол между векторами E₁ и E₂. Если d=p/2, тo cosd=0 и интерференционный член будет равен нулю. Это означает, что волны, поляризованные в двух взаимно перпендикулярных плоскостях интерферировать не могут. Если вторичные источники, от которых наблюдают интерференцию, получены от одного первичного источника, то векторы`E<sub>1</sub> и`E₂ параллельны и cosd=1. В этом случае (3) можно записать в виде

<E²>=<E₁²>+<E₂²>+2<E₁E₂> (5)

где усредняемые по времени функции имеют вид

E₁=E₁₀cos(wt+a), E₂=E₂₀cos(wt+b), (6)

a=-k₁l₁+j₁, b=-k₂l₂+j₂.

Вычислим в начале среднее по времени значение интерференционного члена

(7)

откуда при a=b: <E₁²>=½E²₁₀, <E₂²>=½E²₂₀ (8)

Обозначая I₁=E²₁₀, I₂=E²₂₀ и , формулу (5) можно записать в терминах интенсивности волн. Если источники некогерентны, то

I=I₁+I₂, (9)

а если когерентны, то

I=I₁+I₂+2cosDj (10)

где

Dj=a-b=k₂l₂-k₁l₁+j₁-j₂ (11)

есть разность фаз складываемых волн. Для источников. полученных от одного первичного источника j₁=j₂, поэтому

Dj=k₂l₂-k₁l₁=k₀(n₂l₂-n₁l₁)=(2p/l₀)D (12)

где К₀=2p/l - волновое число в вакууме, D - оптическая разность хода лучей 1 и 2 от S₁ и S₂ до точки наблюдения интерференции 0. Получили

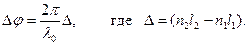(13)

Из формулы (10) следует, что в точке 0 будет максимум интерференции, если cos Dj = 1, откуда

Dj=2pm, или D=ml₀ (m=0,1,2,…) (14)

Условие минимума интерференции будет при cos Dj = -1, откуда

Dj=2p(m+½), или D=(m+½)l₀ (m=0,1,2,…) (14)

Таким образом, волны в точке наложения усилят друг друга, если их оптическая разность хода равна четному числу полуволн ослабят друг друга

если она равна нечетному числу полуволн.

Степень когерентности излучения источника. Интерференция частично когеретных волн.

Реальные световые пучки, приходящие в точку наблюдения интерференции, частично когерентны, т.о. содержат когерентный и некогерентный свет. Для характеристики частично когерентного света вводят степень когерентности 0 < g < 1 которая представляет собой долю некогерентного света в световом пучке. При интерференции частично когерентных пучков получим

I=g×I_неког+(1-g)×I_ког=g×(I₁+I₂)+(1-g)(I₁+I₂+2ÖI₁I₂ cosDj (16)

Откуда I=I₁+I₂+2ÖI₁I₂ cosDj (17)

Если g=0 или g=1, то приходим к случаям некогерентного и когерентного сложения интерферентностей волн.

Опыт Юнга (деление волнового фронта)

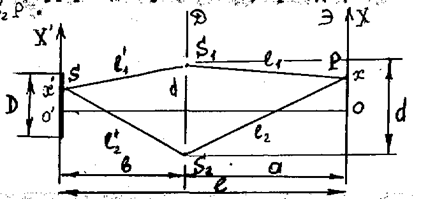Первый опыт по наблюдению интерференции был осуществлен Юнгом (1802). Излучение от точечного источника S проходило через два точечных отверстия S₁ и S₂ в диафрагме D и в точке Р на экране Э наблюдалась интерференция лучей 1 и 2, проходящим по геометрическим путям SS₁P и SS₂P.

Рассчитаем интерференционную картину на экране. Геометрическая разность хода лучей 1 и 2 от источника S до точки Р на экране равна

Dl=(l`<sub>2</sub>+l<sub>2</sub>) - (l`₁+l₁)= (l`<sub>2</sub>-1`₁)+(l₂-l₁) (1)

Пусть d – расстояние между S₁ и S₂, b – расстояние от плоскости источника S до диафрагмы Д, a – расстояние от диафрагмы Д до экрана Э, x – координата точки P на экране отностительно его центра, а x` - координата источника S относительно центра плоскости источника. Тогда согласно рисунку по теореме Пифагора получим

(2)

Аналогичными будут выражения для l`<sub>1</sub> и l`₂, если заменить aàb, xàx`. Предположим, что d и x<<a, тогда

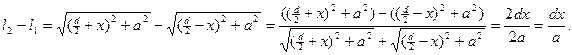(3)

Аналогично (4)

С учетом (3) и (4) геометрическая разность хода лучей 1 и 2 будет равна

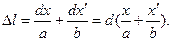(5)

Если лучи 1 и 2 проходят в среде с показателем преломления n, то их оптическая разность хода равна

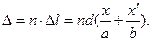
Условия максимумов и минимумов интерференции на экране имеют вид

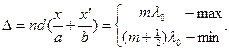(7)

Откуда координаты максимумов х=х_m и минимумов х=х'_m интерференционной картины на экране

(8)

Если источник имеет вид полоски с координатой x', перпендикулярной плоскости рисунка, то изображение на экране также будет иметь вид полосок с координатой х, перпендикулярных плоскости рисунка.

Расстояние между ближайшими максимумами и минимумами интерференции или ширина интерференционных полос (темных или светлых) будет согласно (8) равна

Dx=x_m+1-x_m=x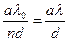`<sub>m+1</sub>-x`_m= (9)

где l=l₀/n – длина волны в среде с показателем преломления n.

Пространственная когерентность(некогерентность) излучения источника

Различают пространственную и временную когерентность излучения источника. Пространственная когерентность связана с конечными (неточечными) размерами источника. Онa поводит к уширению интерференционных полос на экране и при некоторой ширине источника D полному исчезно­вению интерференционной картины.

Объясняется пространственная некогерентность следующим образом. Если источник имеет ширину D, то каждая светящаяся полоска источника с координатой х' даст на экране свою интерференционную картину. В ре-зyльтaтe различные смещенные относительно друг друга интерференционные картины на экране наложатся, друг на друга, что приведет к размазыванию интерференционных полос и при некоторой ширине источника D к полному исчезновению интерференционной картины на экране.

Можно показать, что интерференционная картина на экране исчезнет, если угловая ширина источника, j=D/l, видимая из центра экрана, больше отношения l/d:

(1)

К схеме Юнга сводится метод получения вторичных источников S₁ и S₂ с помощью бипризмы Френеля. Источники S₁ и S₂ лежат в одной плоскости с первичным источником S.

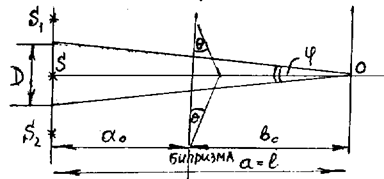
Можно показать, что расстояние между источниками S₁ и S₂, полученными с помощью бипризмы с преломляющим углом Q и показателем n равно

d=2a₀(n-1)q, (2)

а ширина интерференционных полос на экране

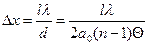(3)

Интерференционная картина на экране исчезнет при выполнении условия 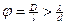или при ширине источника, равной 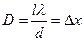, т.е. ширине интерференционной полосы. Получим с учетом (3)

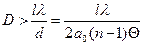(4)

Если l=0,5 м, а₀=0,25 м, n= 1,5 - стекло, l=6 10^-7 - длина волны зеленого света, то ширина источника, при которой исчезнет интерференционная картина на экране равна D=0,2 мм.

Временная когерентность излучения источника. Время и длина когерентности.

Временная когерентность связана со немонохроматичноотью излучения источника. Она приводит к уменьшению интенсивности интерференционных полос при удалении от центра интерференционной картины и последующему ее обрыву. Например, при наблюдении интерференционной картины с использованием немонохроматического источника и бипризмы Френеля на экране наблюдается от 6 до 10 полос. При использовании высокомонохроматичного лазерного источника излучения число интерференционных полос на экране достигает нескольких тысяч.

Найдем условие обрыва интерференции из-за немонохроматичности источника, излучающего в интервале длин волн (l, l+Dl). Положение m-го максимума на экране определяется условием

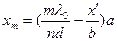(1)

где l=l₀/n - длина волны с показателем преломления n. Отсюда следует, что каждой длине волны l соответствует своя интерференционная картина. При увеличении l происходит смещение интерференционой картины тем большее, чем больше порядок интерференции (номер интерференционной полосы) m. В результате может оказаться, что m-ый максимум для длины волны l+Dl наложится на (m+1)-ый максимум для длины волны l. При этом интерференционное поле между m-ым и (m+1)-ым максимумами для длины волны l равномерно заполнится интерференционными максимумами из интервала (l, l+Dl) и экран окажется равномерно освещенным, т.е. ИК оборвется.

Условие обрыва интерференционной картины

X_max(m,l+Dl)=X_max(m+1,l) (2)

Откуда согласно (1)

(m+1)l=m(l+Dl), (3)

что дает для порядка интерференции(номера интерференционной полосы), при которой произойдет обрыв ИК

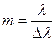(4)

Условие интерференционных максимумов связано с оптической разностью хода лучей 1 и 2, приходящих в точку наблюдения интерференции на экране условием

D=ml (5)

Подставляя (4)в (5), найдем оптическую разность хода лучей 1 и 2, при которой происходит исчезновение интерференции на экране

(6)

При D>L_ког интерференционная картина не наблюдается. Величина L_ког=l²/Dl называется длиной (продольной) когерентности, а величина

t_ког=L_ког/c (7)

- временем когерентности. Переформулируем (6) в терминах частоты излучения. Учитывая, что l=c/n, получим

|dl|= или Dl= (8)

Тогда согласно (6)

L_ког=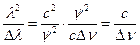 (9)

А согласно (7)

или (10)

Получили связь между временем когерентности t_ког и шириной частотного интервала Dn излучения источника.

Для видимого диапазона (400-700) нм с шириной интервала Dl=300 нм при средней длине волны l= 550 им длина когерентности составляет

порядка L_ког=10^-6 м,а время когерентности порядка t_ког=10^-15 с. Длина когернтности лазерного излучения может достигать нескольких километров. Отметим, что время излучения атома имеет порядок 10^-8 c, а длины волновых цугов составляют порядка L = 3 м.

Принципы Гюйгенса и Гюйгенса-Френеля.

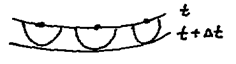В волновой оптике существует два принципа: принцип Гюйгенса и принцип Гюйгенса-Френеля. В принципе Гюйгенса постулируется, что каждая точка фронта волны является источником вторичных волн. Построив огибающую этих волн, можно найти положение фронта волны в последующие моменты времени.

Принцип Гюйгенса является чисто геометрическим и позволяет вывеcти. например, законы отражения и преломления света, объясняет явления распространения света в анизотропных кристаллах(двойное лучепреломление). Но он не может объяснить большинство оптических явлений, обусловленных интерференцией волн.

Френель дополнил принцип Гюйгенса условием интерференции вторич­ных волн, исходящих от фронта волны. Такое расширение принципа Гюйгенса получило название принципа Гюйгенса-Френеля.

Зоны Френеля.

Френель предложил простой прием вычисления результата интерференции вторичных волн. приходящих от фронта волны в произвольную точку Р, лежащую на прямой, проходящую через источник S и точку Р.

Рассмотрим идею Френеля на примере сферической волны, испускаемой точечным источником S.

Пусть фронт волны от источника S в некоторый момент времени находится на расстоянии a от S и на расстоянии b от точки Р. Разобьем фронт волны на кольцевые зоны так, чтобы расстояние от краев каждой зоны до точки Р отличались на l/l. При таком построении колебания в соседних зонах сдвинуты по фазе на p, т.е. происходят в противофазе. Если обозначить амплитуды колебаний в зонах E₁, E₂,... причем E₁>E₂>..., то амплитуда результирующего колебания в точке Р будет равна

E=E₁-E₂+E₃-E₄+… (1)

Здесь чередование знаков (+) и (-), так как колебания в соседних зонах происходят в противофазе. Представим формулу (1) в виде

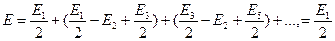(2)

где положено E_m=(Е_m-1 + Е_m+1)/2. Получили, что амплитуда колебаний в точке Р, если в нее приходят колебания от всего волнового фронта, равна Е=Е₁/2, т.е. равна половине амплитуды волны, приходящей в точку Р от первой зоны Френеля.

Если закрыть все четные или нечетные зоны Френеля с помощью специальных пластинок, называемых зонными, то амплитуда колебаний в точке Р увеличится и будет равна

E=E₁+E₃+E₅+…+E_2m+1, E=|E₂+E₄+E₆+…+E_2m+…| (3)

Если на пути фронта волны поставить экран с отверстием, который открывал бы конечное четное число зон Френеля, то интенсивность света в точке Р будет равна нулю

E=(E₁-E₂)+(E₃-E₄)+(E₅-E₆)=0 (4)

\\ \\ \\

0 0 0

т.е. в этом случае в точке Р будет темное пятно. Если же открыть нечет­ное число зон Френеля, то в точке Р будет светлое пятно:

E=E₁-E₂+E₃-E₄+E₅=E₁ (4)

Для перекрытия зон френеля с помощью экранов или зонных пластине необходимо знать радиусы зон френеля. Согласно рис. Получим

r²_m=a²-(a-h_m)²=2ah_m (6)

r²_m=(b+m^l/₂)²-(b+h_m)²=bml-2bh_m (7)

где пренебрегли членами с l² и h_m².

Приравнивая (5) и (6), получим

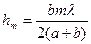(8)

Подставляя формулу (8) в (6), радиус m-ой зоны Френеля

(9)

где м=1,2,3,... - номер зоны Френеля, l - длина волны, излучения, испускаемого источником. Если фронт водны плоский (a ->¥), то

(10)

При фиксированном радиусе отверстия в экране, поставленом на пути волны число m зон Френеля, открываемых этим отверстием, зависит от расстояний a и b от отверстия до источника S и точки Р.

Дифракция волн(света).

Дифракцией называют совокупность интерференционных явлений, наблюдаемых в средах с резкими неоднородностями, соизмеримыми с длиной волны, и связанных с отклонением законов распространения света от законов геометрической оптики. Дифракция, в частности, приводит к огибанию волнами препятствий и проникновению света в область геометрической тени Роль неоднородностей среды могут играть щели, отверстия и различные препятствия: экраны, атомы и молекулы вещества и т.п.

Различают два вида дифракции. Если источник и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку наблюдении, практически параллельны, то говорят о дифракции Фраунгофера(дифракция в параллельных лучах), в противном случае говорят о дифракции Френеля(дифракция в сходящихся лучах)

Дифракция Френеля на круглом отверстии.

Пусть сферическая волна, от источника в падает на круглое отверстие в диафрагме. В этом случае на экране будет наблюдаться дифракционная картина в виде светлых и темных колец.

Если отверстие открывает четное число зон Френеля, то в центре дифракционной картины будет темное пятно, а если оно открывает нечетное число зон Френеля, то светлое пятно.

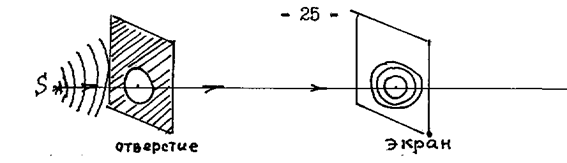
При перемещении диафрагмы с отверстием между источником и экраном в пределах отверстия будет укладываться то четное, то нечетное число зон Френеля и вид дифракционной картины(то с темным, то со светлым пятном в центре) будет постоянно меняться.

Дифракция Фраунгофера на щели.

Пусть от источника S распространяется сферическая волна. С помощью линзы Л₁ она превращается в плоскую волну, которая падает на щель шириной b. Лучи, дифрагировавшие на щели под углом j собираются на экране, находящемся в фокальной плоскости линзы Л₂, в точке F

Интенсивность дифракционной картины в точке Р экрана определяется интерференцией вторичных волн, исходящих от всех элементарных участков щели и распространяющихся в точку Р в одной и том же направлении j.

В виду того, что на щель падает плоская волна, фазы колебаний во всех точках щели одинаковы. Интенсивность в точке Р экрана, обусловленная волнами, распространяющимися в направлении j, будет определяться сдвигом фаз между волнами, исходящими от плоского фронта волны АВ, перпендикулярного направлению распространения волны(см. рис.), либо волнами. исходящими от любой плоскости, параллельной направлению АВ.

Сдвиг фаз между волнами, испускаемыми полоской 0 в центре щели и полоской с координатой х, отсчитанной от центра щели, составляет kx×sinj (рис.). Если щель имеет ширину b и испускает волну с амплитудой E₀, то полоска с координатой x и шириной dx испускает волну с амплитудой (Eo/b)dx. От этой полоски в точку Р экрана в направлении j придет волна с амплитудой

(1)

Множитель iwt, одинаковый для всех волн, приходящих в точку Р экрана, можно опустить, так как при вычислении интенсивности волны в точке Р он исчезнет. Амплитуда результирующего колебания в точке Р, обусловленная наложением вторичных волн, пришедших в точку Р от всей щели, будет равна

(2)

Откуда

(2)

где u=(k^b/₂)sinj=(p^b/_l)sinj, l - длина волны, испускаемая источником. Интенсивность волны I=E² в точке Р экрана будет равна

(3)

где I₀ - интенсивность волны, испускаемой щелью в направлении j=0, когда (sin u/u)=1.

В точке Р будет минимум интенсивности, если sin u=0 или

откуда b×sinj=ml, (m=1,2,…) (4)

Это условие дифракционных минимумов темных полос на экране).

Условие дифракционных максимумов найдем, взяв производную oт I(j) но u и приравняв ее к нулю, что приводит к трансцендентному уравнению tg u=u. Решить ато уравнение можно графически

Согласно рис. прямая y=u пересекает кривые y=tg u примерно в точках с координатой по оси абцисс, равной

u=(2m+1)^p/₂=(m+½)p, а также u=0 à j=0, (5)

что позволяет написать приближенное, но достаточно точное решение уравнения tg u=u в виде

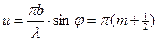(6)

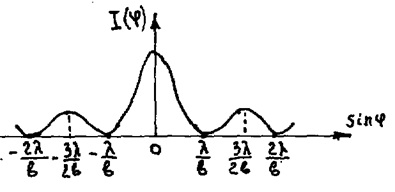Откуда получим, что условие дифракционных максимумов(светлых полос на экране) имеет вид

b×sinj=(m+½)l; (m=1,2,…). (7)

Центральный максимум при j=0 не входит в условие (7)

Распределение интенсивность на экране при дифракции света на одной щели представлено на рис.

Дифракционная решетка и ее применение для разложения немонохроматического излучения источника в спектр.

Дифракционной решеткой можно считать любое устройство, обеспечивающее пространственную периодическую модуляцию падающей на нее световой волны по амплитуде и фазе. Примером дифракционной решетки является периодическая система. N параллельных щелей, разделенных непрозрачными промежутками, лежащих в одной плоскости, расстояние d между серединами соседних щелей называется периодом или постоянной решетки.

Дифракционная решетка обладает способностью разлагать немонохроматической излучение источника в спектр, создавая на экране смещенные относительно друг друга дифракционные картины, соответствующие разным длинам волн излучения источника.

Рассмотрим вначале формирование дифракционной картины для излучения источника с фиксированной длиной волны l.

Пусть на решетку нормально падает плоская монохроматическая волна с длиной волны l, а дифракционная картина наблюдается на в фокальной плоскости линзы Л. Дифракционная картина на экране представляет собой многолучевую интерференцию когерентных пучков света одинаковой интенсивности, идущих в точку наблюдения Р от всех щелей в направлении j.

Для расчета интерференционной картины(ИК) обозначим E₁(j) амплитуду волны (формула (2) предыдущего раздела), пришедшей в точку наблюдения Р от первого структурного элемента решетки, амплитуду волны от второго структурного элемента Е₂=E₁e^id, от третьего Е₂=E₁e^2id и т.д. где

d=k×a×sinj=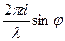 (1)

- сдвиг фаз волн, приходящих в точку Р от соседних щелей с расстоянием d между ними.

Полная амплитуда колебаний, создаваемых в точке Р волнами, прихо­дящими в нее от всех N щелей дифракционной решетки, представляется суммой геометрической прогрессии

E_P=E₁(j)(1+e^id+e^2id+…+e^i(N-1)d)=E₁(j) (2)

Интенсивность волны в точке Р равна I(j)=E_pE^*_p, где E^*_p - комплексно сопряженная амплитуда. Получаем

I(j)=I₁(j)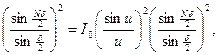 (3)

где обозначено

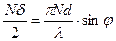, (4)

Отсюда следует, что распределение интенсивности на экране I(j), создаваемое излучением от N₁₂ щелей, промодулировано функцией интенсивности одной щели I₁(j)=I₀(sin(u)/u)². Распределение интенсивности на экране, определяемое формулой (3) представлено на рис.

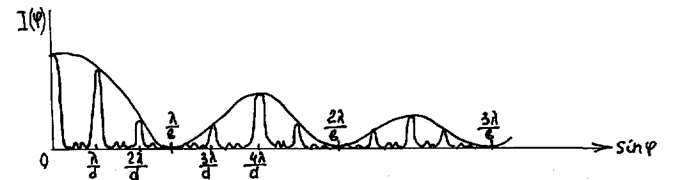
Из рисунка видно, что в ИК имеются резкие максимумы, называемые главными, между которыми наблюдаются малоинтенсивные максимумы и минимумы, называемые побочными. Число побочных минимумов равно N-1, а число побочных максимумов равно N-2. Точки, в которых I₁(j)= 0, называются главными минимумами. Их расположение такое же как и в случае одной щели.

Рассмотрим формирование главных максимумов. Они наблюдаются в направлениях, определяемым условием sind/2=0 (но при этом sin Nd/2=0, что приводит к неопределенности I(j)=0/0¹0. Условие sind/2=0 дает d/2=pk или

d×sinj=kl, k=0,±1,±2,… (5)

где k - порядок главного максимума.

Рассмотрим формирование минимумов. Первое условие sin u=0 при u¹0 приводит к условию главных минимумов, такому же как в случае одной щели

b×sinj=ml, m=0,±1,±2,… (6)

Второе условие sin Nd/2=0 при sin d/2¹0 определяет положение побочных минимумов при значениях

p, … (N-1)p;

Np, (N+1)p, … (2N-1)p; (7)

2Np, (2N+1)p,… (3N-1)p;

Подчеркнутые значения кратны N и приводят к условию главных максимумов Nd/2 =Nkp или d/2=kp. Эти значения d должны быть исключены из списка побочных минимумов. Оставшиеся значения можно записать в виде

, где р - целое число, некратное N (8)

откуда получаем условие побочных минимумов

d×sinj=(k+^P/_N)l, P=0,±1,±2,…N-1 (9)

где k - фиксированный порядок главного максимума. Можно допустить отрицательные значения р= -1, -2,... -(N-1), которые дадут положение побочных минимумов слева от k-го главного максимума.

Из условий главных и побочных максимумов и минимумов следует, что излучению с другой длиной волны l будет соответствовать другое угловое расположение минимумов и максимумов в дифракционной картине. Это означает, что дифракционная решетка осуществляет разложение немонохроматического излучения источника в спектр.

Характеристики спектральных приборов: угловая и линейная дисперсии и разрешающая способность прибора.

Любой спектральный прибор осуществляет разложения излучения на монохроматические составляющие путем их пространственного разделения с помощью диспергирующего элемента(призмы, дифракционной решетки и т.д.) Чтобы извлечь необходимую информацию из наблюдаемых спектров, прибор должен давать хорошее пространственное разделение спектральных линий, а также обеспечивать возможность раздельного наблюдения близких спектральных линий.

В связи с этим для характеристики качества спектрального прибора вводят следующие величины: угловую D_j =dj/dl или линейную D_l =dl/dl дисперсии прибора и его разрешающую способность R=l/Dl, где Dl - минимальная разность длин волн спектральных линии, которые прибор позволяет видеть раздольно. Чем меньше разность Dl, "видимая" прибором, тем выше его разрешающая способность R.

Угловая дисперсия D_j определяет угол Dj=D_jDl, на который разводит прибор две спектральные линии, длины волн которых отличаются на единицу (например, в оптике полагают Dl = 1 нм). Линейная дисперсия D_l определяет расстояние Dl =D_lDl между спектральными линиями на экране, длины волн которых отличаются на единицу (Dl =1 нм). Чем выше значения Dj и D_l способность спектрального прибора к пространственному разделению спектральных линий.

Конкретные выражения для дисперсий прибора D_j и D_l и его разрешающей способности R зависят от типа прибора, используемого для регистрации спектров излучения различных источников. В данном курсе вопрос о вычислении спектральных характеристик прибора будет рассмотрен на примере дифракционной решетки.

Угловая и линейная дисперсии дифракционной решетки.

Выражение для угловой дисперсии дифракционной решетки можно найти дифференцируя условие главных максимумов d sinj = kl по l. Получим dcosj dj=kdl, откуда

(1)

Вместо угловой дисперсии можно использовать линейную

(2)

Учитывая, что положение спектральной линии, отсчитываемое от центра дифракционной картины равно l=F×tgj, где F - фокусное расстояние линзы в фокальной плоскости которой регистрируется спектр, получим

, что дает (3)

Разрешающая способность дифракционной решетки.

Большая угловая дисперсия является необходимым, но недостаточным условием раздельного наблюдения близких спектральных линий. Это объ­ясняется тем, что спектральные линии имеют ширину. Любой детектор (в том числе и глаз) регистрирует огибающую спектральных линий, кото­рые в зависимости от их ширины могут восприниматься либо как одна, либо как две спектральные линии.

В связи с этим вводится дополнительная характеристика спектрального прибора - его разрешающая способность: R=l/Dl, где Dl - минимальная разность длин волн спектральных линий, которые прибор позволяет видеть раздельно.

Чтобы получить конкретное выражение для R для данного прибора, необходимо задаться критерием разрешения. Известно, что глаз воспринимает две линии раздельно, если глубина "провала" в огибающей спектральных линий составляет не менее 20% от интенсивности в максимумах спектральных линий. Этому условию удовлетворяет критерий, предложенный Рэллеем: две спектральные линии одинаковой интенсивности можно наблюдать раздельно, если максимум одной из них совпадает о "краем" другой. За "края" линии можно принять положение ближайших к ней побочных минимумов.

На рис. изображены две спектральные линии, соответствующе излучениям с длиной волны l₁<l₂.

Совпадение "края" одной линии с максимумом другой эквивалентно одинаковому угловому положению j, например, максимума, левой линии, соответствующей длине волны l₁, и левого "края" линии, соответствующей длине волны l₂.

Положение k-го максимума спектральной линии с длиной волны l₁ определяется условием

d×sinj=kl₁ (1)

Положение левого"края" линии с длиной волны l₂ определяется угловым положением ее первого левого побочного минимума (р=-1)

d×sinj=(k-¹/_N)l₂ (2)

Приравнивая правые части формул (1) и(2), получим

Kl₁=(k-¹/_N)l₂, или k(l₂-l₁)=l₂/N, (3)

Откуда

(4)

Получили, что разрешающая способность R=kN дифракционной решетки увеличивается с увеличением числа N штрихов на решетке, а при фиксированном N с увеличением порядка k спектра.

Тепловое излучение.

Тепловое излучение(ТИ) - это испускание ЭМ-волн нагретым телом за счет его внутренней энергии. Все остальные виды свечения тел, возбуждаемые за счет видов энергии, отличие от тепловой, называют люминесценцией.

Поглащательная и отражательная способность тела. Абсолютно черное, белое и серое тела.

В общем случае любое тело отражает, поглощает и пропускает падающее на него излучение. Поэтому для падающего на тело потока излучения можно написать:

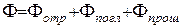(1)

откуда:

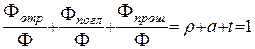(2)

где r, а, t - коэффициенты отражения, поглощения и пропускания, называемые также его отражательной, поглащательной и пропускательной способностями. Если тело не пропускает излучение, то t=0, и r+a=1. В общем случае коэффициенты r и а зависят от частоты излучения n и температуры тела: 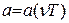и .

Если тело полностью поглощает падающее на него излучение любой частоты, но не отражает его (а_T = 1,), то тело называют абсолютно чёрным, а если тело полностью отражает излучение, но не поглощает его, то тело называют белым, если же а_T<1, то тело называют серым. Если поглащательная способность тела зависит от частоты или длины волны падающего излучения и a_{n, T} <1, то тело называют селективным поглотителем.

Энергетические характеристики излучения.

Поле излучения принято характеризовать потоком излучения Ф (Вт).

Поток - это энергия, переносимая излучением через произвольную поверхность в единицу времени. Поток излучения, испускаемый единицей площади. тела, называют энергетической светимостью тела и обозначают R_T (Вт/м³).

Энергетическую светимость тела в интервале частот 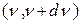обозначают dR_n, а если она зависит от температуры тела T, тo dR_n,T. Энергетическая светимость пропорциональна ширине dn частотного интервала излучения: . Коэффициент пропорциональности 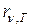называют испускательной пособностью тела или спектральной энергетической светимостью.

Размерность .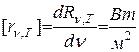

Энергетическая светимость тела во всем интервале испускаемых частот излучения равна

Связь между спектральными характеристиками излучения по частоте и длине волны.

Характеристики излучения, зависящие от частоты n или длины волны l излучения, называют спектральными. Найдем связь между этими харак­теристиками по длине и частоте волны. Учитывая, dR_n=dR_l, получим: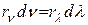. Из связи n=с/l следует |dn|=(c/l²)dl. Тогда

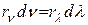
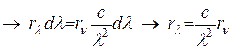
Тепловое излучение. Законы Вина и Стефана-Больцмана.

Тепловое излучение - это ЭМ-излучение, испускаемое веществом за счет его внутренней энергии. ТИ имеет сплошной спектр, т.е. его испускательная способность r_n,T или r_l,T в зависимости от частоты или длины волны излучения изменяется непрерывно, без скачков.

ТИ - это единственный вид излучения в природе, которое является равновесным, т.е. находится в термодинамическом или тепловом равновесии с излучающим его телом. Тепловое равновесие означает, что излучающее тело и поле излучения имеют одинаковую температуру.

ТИ является изотропным, т.е. вероятности испускания излучения разных длин волн или частот и поляризаций в разных направлениях равновероятны (одинаковы).

Среди излучающих (поглощающих) тел особое место занимают абсолютно черные тела (АЧТ), которые полностью полащают падающее на него излучение, но не отражают его. Если АЧТ раскалить, то, как показывает опыт, оно будет светить ярче, чем серое тело. Например, если на фарфоровой тарелке нанести рисунок желтой, зеленой и черной краской, а затем тарелку нагреть до высокой температуры, то черный рисунок будет светить ярче, зеленый слабее, и совсем слабо будет светиться желтый рисунок. Примером раскаленного АЧТ является Солнце.

Другим примером АЧТ является полость с малым отверстием и зеркально отражающими внутренними стенками. Внешнее излучение, попав в отверстие, остается внутри полости и практически не выходит из него, т.е. поглощательная способность такой полости равна единице, а это и есть АЧТ. Например, обычное окно в квартире, открытое в солнечный день, не выпускает наружу попавшее внутрь его излучение, и снаружи кажется черным, т.е. ведет себя как АЧТ.

Опыт показывает, что зависимость испускательной способности АЧТ от длины волны излучения l имеет вид:

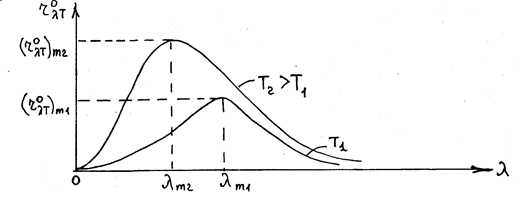
График имеет максимум. При увеличении температуры тела максимум зависимости от l смещается в сторону более коротких длин волн (больших частот), а тело начинает светить ярче. Это обстоятельство отражено в двух опытных законах Вина и законе Стефана-Больцмана.

Первый закон Вина утверждает: положение максимума испускательной способности АЧТ (r^o_l,T)_m обратно пропорционально его температуре:

(1)

где b = 2,9×10^-3 м×К - первая постоянная Вина.

Второй закон Вина утверждает: максимальная испускательная способность АЧТ пропорциональна пятой степени его температуры:

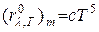(2)

где с = 1,3×10^-5 Вт/м³К⁵ - вторая постоянная Вина.

Если вычислить площадь под графиком испускательной способности АЧТ, то найдем его энергетическую светимость R^o_T. Она оказывается пропорциональной четвертой степени температуры АЧТ. Таким образом

(3)

Это закон Стефана-Больцмана, s = 5,67×10^-8 Вт/м²К⁴ - постоянная Стефана-Больцмана.

Закон Кирхгофа.

Кирхгофом было доказано следующее свойство тепловых излучателей:

отношение испускательной способности тела r_l,T к его поглащательной способности a_l,T при той же температуре T не зависит от природы из­лучающего тела, для всех тел одинаково и равно испускательной способно­сти АЧТ r^o_l,T: r_l,T/a_l,T =r^o_l,T.

Это основной закон теплового излучения. Для его доказательства рассмотрим теплоизолированную полость А с малым отверстием, внутри ко­торой находится тело В. Полость А нагрета и обменивается теплом с телом В через поле излучения полости С. В состоянии теплового равновесия тем­пературы полости А, тела В и поля излучения С одинаковы и равны Т. В опыте имеется возможность измерять поток

e_l,T излучения, выходящего из отверстия, свойства которого аналогичны свойствам излучения С внутри полости.

Поток излучения e_l,T, падающий от нагретой полости А на тело В поглащается этим телом и отражается, а само тело В излучает энергию.

В состоянии теплового равновесия испущенный телом В поток r_l,T и отраженный им поток (1-a_l,T)e_l,T должны равняться потоку e_l,T теплового излучения полости

(1)

откуда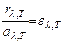

Это и есть закон Кирхгофа. При его выводе природа тела В не учитывалась, поэтому он справедлив для любого тела и, в частности, для АЧТ, для которого испускательная способность равна r^o_l,T, а поглощательная способность a_l,T=1. Имеем:

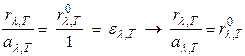(2)

Получили, что отношение испускательной способности тела к его поглощательной способности равно испускательной способности АЧТ при той же температуре Т. Равенство r^o_l,T=e_l,T говорит о том, что по выходящему из полости потоку излучения e_l,T можно измерить испускательную способность АЧТ r^o_l,T.

Формула Планка и доказательство с ее помощью опытных законов Вина и Стефана-Больцмана.

Длительное время различные ученые пытались объяснить закономерности излучения АЧТ и получить аналитический вид функции r^o_l,T. При попытке решить задачу было получено много важных законов теплового излучения. Так, в частности. Вин на основе законов термодинамики показал, что испускательная способность АЧТ r^o_l,T является функцией отношения частоты излучения n и его температуры T, совпадающей с температурой АЧТ:

r^o_l,T =f (n/T)

Впервые явный вид для функции r^o_l,T был получен Планком (1905). При этом Планк предположил, что ТИ содержит ЗМ-волны различных частот (длин волн) в интервале (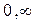). Волну фиксированной частоты n называют осциллятором ЭМ-поля. По предположению Планка энергия каждого осциллятора поля частоты n квантуется, то есть зависит от целочисленного параметра, а значит, изменяется дискретным образом(скачком):

(1)

где e₀(n) - минимальный квант(порция) энергии, которым может обладать осциллятор поля частоты n.

На основе этого предположения Планк получил следующее выражение для испускательной способности АЧТ (см. любой учебник):

(2)

где с = 3×10⁸м/с - скорость света, k=1,38×10^-23 Дж/К - постояннная Больцмана.

В соответствии с теоремой Вина r^o_l,T =f(n/T) необходимо положить, что квант энергии осциллятора поля пропорционален его частоте n:

(3)

где коэффициент пропорциональности h= 6,62×10^-34 Дж×с или 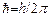=1,02×10^-34 называется постоянной Планка, w = 2pn - циклическая частота излучения (осциллятора поля). Подставив (3) в формулу (2), получим

(4)

или

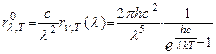(5)

Для практических расчетов удобно подставить значения постоянных c, k, h и записать формулу Планка в виде

(6)

где a₁ = 3,74×10^-16 Вт.м², a₂ = 1,44×10^-2 мК.

Полученное выражение для r^o_l,T дает правильное описание закона излучения АЧТ, соответствующее эксперименту. Максимум функции Планка можно найти вычислив производную dr^o_l,T/dl=0  и приравняв ее к нулю, что дает

(7)

Это первый закон Вина. Подставив l =l_m в выражение для функции Планка, получим

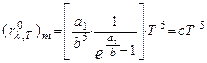(8)

Это второй закон Вина. Интегральная энергетическая светимость (площадь под графиком функции Планка) находится интегрированием функции Планка по веем длинам волн. В результате получим(см. учебник):

(9)

Это закон Стефана-Больцмана. Таким образом, формула Планка объясняет все опытные законы излучения АЧТ.

Излучение серых тел.

Тело, для которого поглощательная способность a_l,T=a_T<1 и не зависит от частоты излучения(его длины волны) называют серым. Для серого тела согласно закону Кирхгофа:

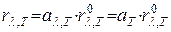, где r^o_l,T - функция Планка

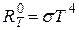, где (1)

Для несерых тел (селективных поглотителей), для которых a_l,T зависит от n или l, связь R_T=a_TR⁰_T не имеет места, и надо вычислять интеграл:

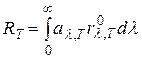(2)

Дата добавления: 2014-01-07