Свойства распределения Максвелла

Каноническое распределение в классическом приближении. Распределение Максвелла и Больцмана

Чтобы определить состояний системы при квантовом рассмотрении, необходимо знать все квантовые числа всех частиц системы, то есть квантовые состоянии всех частиц системы, которые и определяют состояния n системы и ее энергию E_n. При этом вероятность такого состояния будет

P_n(E_n) = e^-En/kT/z

В классическом приближении состояния каждой частицы системы определяются координатами R и импульсом P. Чтобы определить состояние всей системы, нужно знать координаты и импульсы всех частиц системы. Полная энергия системы при этом будет зависеть от координат и импульсов всех ее частиц.

E = E(p,q)

Определим вероятность того, что координаты первой частицы лежат в интервале от R₁ до R ₁ + d R ₁, а ее импульс при этом - в интервале от p ₁ до p ₁ + d p ₁, при этом координаты второй частицы – в интервале от R ₂ до R ₂ + d R ₂, а ее импульс при этом - в интервале от p ₂ до p ₂ + d p ₂ и так далее для всех частиц.

Чтобы вычислить такую вероятность, надо определить, каким квантовым состоянием системы n соответствует рассматриваемый интервал, вычислить вероятность каждого такого состояния и затем сложить. Если рассматриваемые интервалы dp и dq бесконечно малы, то в классическом приближении энергия будет одинакова и будет

P_n(E) = e^-E(p,q)/kT/z

Чтобы вычислить рассматриваемую вероятность, надо взять вероятность одного состояний и умножить на число состояний, при которых частицы системы лежат в интервалах dp и dq.

Чтобы определить число таких состояний, рассмотрим сначала одну частицу в одномерном случае и найдем число состояний, при которых ее координата лежит в интервале от x до x + dx, а проекции импульса - в интервале от p до p + dp.

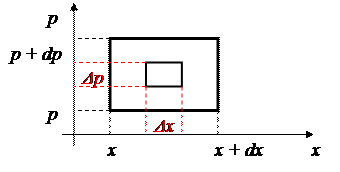
Из квантовой механики известно, что для каждой частицы в этом случае выполняется принцип неопределенности Гайзенберга

ΔpΔx ≈ 2ħΠ

Таким образом, число состояний, при которых импульс и координаты частиц лежат в заданных интервалах будет dpdx/2ħΠ; если ситема состоит из “n” частиц dpdq/(2ħΠ)^3N. И тогда вероятность будет

W(p,q)dpdq = (e^-E(p,q)/kT/z)(dpdq/(2ħΠ)^3N) = c₀ e^-E(p,q)/kTdpdq

Постоянный коэффициент c₀ можно определить из условия нормировки

∫W(p,q)dpdq = 1 = c₀ ∫ e^-E/kTdpdq

Определим вероятность того, что импульс первой частицы лежит в интервале от P₁ до P₁ + dP₁, а импульс второй частицы - от P₂ до P₂ + dP₂ и так далее для импульсов всех частиц при любых значениях их координат.

Чтобы найти эту вероятность, надо полную вероятность просуммировать по всем возможным координатам всех частиц. Тогда

W(p)dp= dp ∫W(p,q)

Полная энергия системы в классическом приближении состоит из кинетической и потенциальной

E(p,q) = T(p) + u(q)

W(p,q)dpdq = dp ∫c₀ e^-E/kTdq = dp ∫c₀ e^-T(p)/kT e^-u(q)/kT dq = dpc₀ e^-T(p)/kT∫e^-u(q)/kT dq = c₁ e^-T(p)/kTdp

Постоянный коэффициент c₁ можно легко определить из условия нормировки. Определим вероятность того, что импульс первой частицы леит в интервале от P ₁ до P ₁ + d P ₁. При любых значениях импульса всех остальных частиц

W₁(p ₁)d p ₁ = dp₁∫W(p)d p ₂ d p ₃ d p _n

Кинетическая энергия системы будет

T(p) = (dp₁²/2m) + ∑(dp_i²/2m)

Тогда

W₁(p ₁)d p ₁ = [c₂ e ^(-p₁²/2mkT)]dp₁

W₁(p ₁) = [c₂ e ^(-p₁²/2mkT)] – распределение Максвелла

Определим вероятность того, что координаты первой частицы лежат в интервале от R ₁ до R ₁ + d R ₁, второй частицы – в интервале от R ₂ до R ₂ + d R ₂ и так далее для всех частиц при любых значениях их импульсов.

W(q)dq = dq ∫W(p,q)dp = dqc₀e^-u(p)/kt ∫ e^-T(p)/kt dp = c₃e^-u(q)/ktdq

Определим вероятность того, что координаты первой частицы лежат в интервале от R до R + dR при любых координатах всех остальных частиц. Потенциальная энергия идеального газа равно сумме потенциальных энергий всех частиц системы. При этом потенциальная энергия каждой частицы зависит только от координат.

u(q) = u₁(R ₁) + ∑u_i

W₁(R ₁)d R ₁ = d R ₁ ∫c₃e^-u(q)/ktd R ₂d R ₃…= c₄ e^{-u(R 1)/kt}d R ₁ – распределение Больцмана

Среднее число частиц f(p)dp, импульс которых лежит в интервале от P до P + dP, будет

f(p)d p = NW₁(p)d p

W₁(p) – плотность вероятности

В § 2.6 было показано, что вероятность того, что одна частица имеет импульс в интервале от P до P + dP, будет

W₁(p)d p = [c₇ e ^(-p₁²/2mkT)]d p

Чтобы определить вероятность того, что скорость одной частицы лежит в интервале от V до d V, сделаем замену переменных p = m V.

W₁(V)d V = [c₇ e ^(-mV²/2kT)]md V = c₈ e ^(-mV²/2kT)d V

Определим вероятность того, что проекция скорости первой частицы лежит в интервале от V до dV

d V = dV_xdV_ydV_z

W₁(V_x)dV_x = dV_x∫ W₁(V)dV_y dV_z = dV_x c₈ e ^(-mV_x²/2kT) ∫ e ^[-m(V_y² + V_z²)/2kT] dV_ydV_z = c₉ e ^(-mV_x²/2kT)dV_x

Постоянный коэффициент можно определить из условия нормировки

c₉ = ∫W₁(V_x)dV_x = 1 = (m/2ПkT)^1/2

W₁(V_x)dV_x = (m/2ПkT)^1/2 e ^(-mV_x²/2kT)dV_x

Точно так же находим проекции на оси y и z.

W₁(V)d V = (m/2ПkT)^3/2 e ^(-mV²/2kT)d V

<V_x> = ∫ V_x W₁(V_x)dV_x = ∫ V_x (m/2ПkT)^1/2 e ^(-mV_x²/2kT)dV_x = 0

Определим вероятность того, что величина скорости лежит в интервале от V до d V. Чтобы определить эту вероятность, надо вероятность W₁(V)d V просуммировать по всем направлениям скорости, то есть

W(V)d V = ∫W₁(V)d V = ∫(m/2ПkT)^3/2 e ^(-mV²/2kT)d V

Перейдем к сферическим координатам

V_x, V_y, V_z → V, θ, φ

Экобиан этого преобразования будет V²sinθ

W(V)dV = ∫(m/2ПkT)^3/2 e ^(-mV²/2kT) V²sinθdVdφdθ =

= 4ПV² (m/2ПkT)^3/2e ^(-mV²/2kT) dV

Чтобы определить наиболее вероятную скорость, надо приравнять у нулю производную

W₁(V)/dV = 0

(d/dv)(V² e ^(-mV²/2kT))= 0

V_m = (2kT/m)^1/2

Определим среднюю скорость

<V> = ∫VW₁(V)dV = (4/П)^1/2 (2kT/m)^1/2

Найдем среднюю квадратичную скорость

<V²> = ∫V²W₁(V)dV = 3kT/m

Дата добавления: 2014-01-07