Теплоемкость газов и твердых тел

Условие применимости классического приближения и вырождения идеального газа

Как известно, среднее число частиц, энергия которых лежит в интервале от E до E + dE, определяется квантовым распределением.

f(E)dE = c₀V(E)^1/2dE/(e^{(E - μ)/kT} ± 1)

“+” – распределение Ферми

“-” – распределение Бозе

V – объем системы

c₀ – можно найти из условия нормировки

∫f(E)dE = N

Это распределение справедливо всегда. В классическом приближении среднее число частиц, скорость которых в интервале от V до V + dV, дается распределением Максвелла.

f(V)dV = 4NП(m/2ПkT)^3/2V²e^(-mV²/2kT)dV

Для идеального газа E = mV²/2

dE = mVdV

f(E)dE = c_o1N(E)^1/2e^-E/kTdE

Сравнивая полученные распределения, заметим, что классическое приближении будет совпадать с квантовым, если e^(E-μ)/kT>>1. Тогда

f(E)dE = c_oV(E)^1/2e^μ/kT e^-E/kT dE

Таким образом, условием применимости классического приближения будет e^E-μ/kT>>1. Это условие должно выполняться для любых значений энергии, в том числе и в самой трудном случае (E = 0). То есть e^-μ/kT>>1.

Рассмотрим классическое приближение

N = ∫ f(E)dE = c_oVe^μ/kT ∫(E)^1/2 e^-E/kT dE = c_o2Ve^μ/kT(kT)^3/2 = N

e^-μ/kT = c_o2V(kT)^3/2/N >>1

T>>(N/c_o2V)^2/3(1/k)

Если Т_сист. > Т _{с(критич)}, где Т_сист = (N/c_o2V)^2/3(1/k), то можно пользоваться классическим приближением. Заметим, что критическая температура определяется концентрацией частиц системы N/V.

Вырожденная система – система, основная часть частиц которой находится в состоянии с минимальной энергией.

Рассмотрим ферми-частицы, функция распределения которых имеет вид

f(E)dE = c_oV(E)^1/2 dE/ (e^(E-μ)/kT + 1)

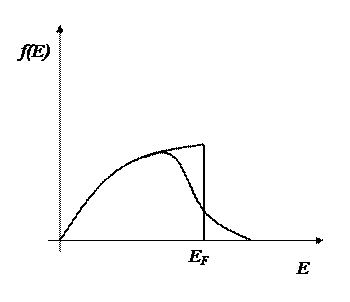
Ферми-газ считается вырожденным, если частиц с энергией E большей, чем E_F, будет мало.

Это условие будет выполняться, если

e^(E-μ)/kT > 1 E > E_F

Наилучший случай, когда μ максимально большое.

e^(E-Ef)/kT >> 1 E > E_F

Определим, чему равняется энергия Ферми. Для этого рассмотрим газ при абсолютном нуле температуры. В этом случае интеграл от 0 до ∞ можно заменить на интеграл от 0 до E_F и учесть, что знаменатель дроби при нулевой температуре будет равен единице. Тогда получается

N = ∫f(E)dE = 2c₀VE_F^3/2 /3

E_F = (3N/2V)^2/3

T_F = (1/k)(3c₀N/2V)^2/3

Рассмотрим систему из Бозе-частиц. На эти частицы не распространяется принцип Паули. Среднее число таких частиц будет

E_l<N_l> = (e^(El-μ)/kT - 1)^-1

Так как на эти частицы не распространяется принцип Паули, то в основном состоянии с E₀ = 0 может быть сколько угодно частиц. В случае вырождения в заданном состоянии должно находится много частиц

<N₀> = (e^-μ/kT - 1)^-1

e^-μ/kT ≈ 1

Среднее число частиц, лежащих в заданном интервале, можно определить с помощью функции распределения Бозе

f(E)dE = c_oV(E)^1/2 dE/ (e^(E-μ)/kT - 1)

Но надо учесть, что сюда не входят частицы с энергией E = 0, так как для этих частиц функция распределения равна нулю.

∫ f(E)dE = Ne – частицы, энергия которых не равна нулю (возбужденные частицы)

Ne = ∫ c_oV(E)^1/2 dE/ (e^(E-μ)/kT - 1)

В случае вырождения e^-μ/kT = 1

Ne = ∫ c_oV(E)^1/2 dE/ (e^E/kT - 1) = c_oV (kT)^3/2 ∫x^1/2dx/(e^x-1) = c_o3V (kT)^3/2

Если газ вырожден, то число возбужденный частиц должно быть меньше полного числа частиц.

c_oV (kT)^3/2 << N

T << (1/k)(N/c_o3V)^2/3 = T_b – температура Бозе

Оказывается, что T_c, T_F, T_b практически определяется одинаковыми функциями.

Если система в результате процессов получает некоторое количество тепла σQ, то теплоемкость равна

с = σQ/dT

dT – изменение температуры системы при этом процессе

Очевидно, что теплоемкость системы зависит от процесса. В газах обычно различают теплоемкость при постоянном объеме c_V и при постоянном давлении c_p. Из первого начала термодинамики

d<E> = σQ + σA

σQ = d<E> - σA

Тогда для идеального газа σA = - pdV

c_V = σQ/ dT = d<E>/dT

<E> = (3/2)NkT

c_V = (3/2)Nk

Если газ многоатомный, то

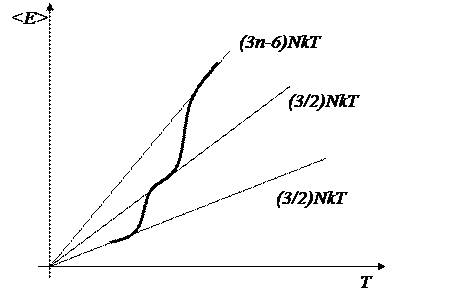
Вычислим c_p при постоянном давлении

c_p = σQ/dT = d<E>/dT - σA/dT

σA = - pdV

pV = NkT

c_p = c_V + Nk

Рассмотрим теплоемкость твердых тел. Твердое тело можно представить, как некоторый замкнутый объем, в котором находится электронный и фононный газ. Фононный газ описывает поведение кристаллической решетки. Теплоемкость твердого тела будет равна сумме теплоемкостей фононного и электронного газа. Рассмотрим теплоемкость твердого тела. Как было показано в § 2.5, энергия фононного газа зависит от температуры.

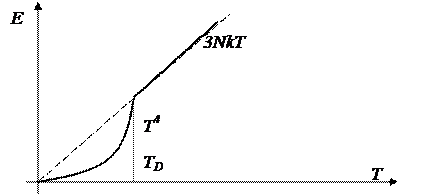
T >> T_b → <E> = 3NkT → c_V = 3Nk

T << T_b → <E> = σT⁴ → c_b = 4 σT³

Рассмотрим теплоемкость электронного газа

<E> = ∫Ef<E>dE

f(E) = g(E)<Ne> = c₀(E)^1/2/(e^(E-μ)/kT + 1)

c_V = ∂<E>/∂T = ∫E∂fdE/∂T

<N> = ∫fdE

∂N/∂T = ∫∂fdE/∂T = 0

c_V = ∫(E – E_F)∂f/∂T = ∫(E – E_F) g(E) [e^(E-μ)/kT(E-μ)/(e^(E-μ)/kT + 1)²kT²]dE

Рассмотрим функцию

e^(E-μ)/kT/(e^(E-μ)/kT + 1)²= <Ne>(1 - <Ne>) = (e^(E-μ)/kT + 1)^-1[1 - (e^(E-μ)/kT + 1)^-1]

Если рассмотреть случай низких температур, то полученное выражение будет отлично от нуля лишь в очень узкой области значений энергии вблизи E_F. Поэтому значения энергий в подынтегральном выражении должны быть близки к E_F, а химический потенциал при низких температурах μ ≈ E_F.

c_V = g(E_F)(1/KT²)∫[(E - EF)² e^(E-μ)/kT/(e^(E-μ)/kT + 1)²]dE = αT

α = const

Таким образом, при низких температурах, когда T << T_F, c_V = αT

При высоких температурах, T >> T_F, можно пользоваться классическим приближением и рассматривать электроны, как одноатомный идеальный газ, средняя энергия которого <E> = 3NkT/2, c_V = 3Nk/2.

Дата добавления: 2014-01-07