Общая постановка транспортной задачи

Задача о перевозках.

ТРАНСПОРТНАЯ ЗАДАЧА.

Симплекс-методом можно решить любую ЗЛП. Но есть такие ЗЛП, которые можно решить более простыми методами. К таким задачам относится транспортная задача. Примером транспортной задачи является задача о перевозках, задача о назначениях, задача развития и размещения одно- и многопродуктовых отраслей.

Имеется m пунктов отправления А₁, А₂,..., А_m, в которых сосредоточен некоторый груз в количествах а₁,а₂,...,а_m и n пунктов назначения В₁, В₂,..., В_n, в которые требуется завезти этот груз в количествах b₁,b₂,...,b_n, причем

. Известны стоимости c_ij перевозки единицы

груза из пунктов А_i в пункты В_j (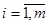; 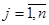). Предполагается, что

а) товар является однородным и делимым, т.е. потребителю безразличен источник получаемого товара, а перевозки могут осуществляться партиями любого размера;

б) стоимость перевозки груза из одного пункта в другой пропорциональна количеству перевозимого груза.

Требуется составить такой план перевозок из пунктов А_i в пункты В_j, при котором затраты на перевозки были бы наименьшими.

Исходные данные задачи обычно представляются в виде транспортной таблицы (табл. 5.1).

Таблица 5.1

Пн По	В1	В2	...	В3	Запасы
А1	^С11	^С12	...	^С1n	а1
А2	^С21	^С22	...	^С2n	а2
...	...	...	...	...	...
Аm	^Сm1	^Сm2	...	^Сmn	аm
Потребности	в1	в2	...	вn

Стоимости c_ij проставляются в правых верхних углах соответствующих клеток.

Составим математическую модель задачи. Пусть x_ij – количество груза, перевозимого из пункта А_i в пункт В_j. Целевая функция задачи (общая стоимость перевозок) записывается следующим образом:

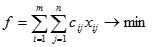
Систему ограничений записываем, руководствуясь тем, что:

а) запасы пунктов отправления должны быть исчерпаны;

б) потребности пунктов назначения должны быть удовлетворены;

в) перевозки могут быть только неотрицательными.

Таким образом, ограничения задачи имеют вид:

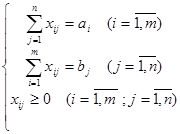
Мы видим, что задача о перевозках является ЗЛП.

Транспортной задачей называется ЗЛП следующего вида:

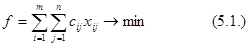
Отметим следующую особенность транспортной задачи как ЗЛП специального вида: система уравнений разбита на две группы (5.2) и (5.3) так, что каждая переменная входит ровно в одно уравнение группы с коэффициентом 1.

Уравнения (5.2) называются горизонтальными, уравнения (5.3) -вертикальными.

Любой набор значений переменных x_ij называется планом перевозок. План перевозок называется допустимым, оптимальным или опорным, если он является допустимым, оптимальным или опорным планом ЗЛП (5.1 - 5.4).

Транспортная задача, как и любая задача линейного программирования, может быть решена симплекс-методом. Однако
благодаря указанной выше особенности транспортной задачи, для неё
существуют более простые методы решения, один из которых – метод
потенциалов - мы изучим.

Дата добавления: 2014-01-07