Алгоритм решения транспортной задачи методом потенциалов

1. Отыскиваем исходный опорный план перевозок (к примеру, методом минимального элемента). Переход к пункту 2.

2. Строим систему потенциалов. Для этого для каждой базисной
клетки (p,q) записываем уравнение α_p+β_q=c_pq. Получается
система m+n–1 уравнений с m+n неизвестными потенциалами. Один из
потенциалов полагаем равным 0 и находим из системы остальные
потенциалы. Переход к пункту 3.

3. Для каждой свободной клетки (i, j) вычисляем псевдостоимость 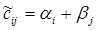. Если для всех свободных клеток , то план оптимален, и алгоритм останавливается. Если же найдется свободная клетка (i, j), для которой 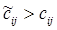, то переход к пункту 4.

4. Строим цикл пересчета, проходящий через клетку (i, j),
делаем по нему максимально допустимый сдвиг, получив, таким образом,
новый опорный план. Переход к пункту 2.

Пример. Исходные данные задачи приведены в таблице 5.9.

Методом минимального элемента находим исходный опорный план перевозок и записываем его в ту же таблицу.

Таблица 5.9

Пн По	В1	В2	В3	В4	Запасы	αi
А1	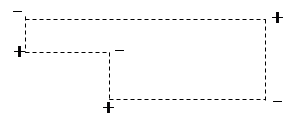^2 15	^1 4	^5 7	^11 6
А2	^5 7	^4 18	^8	^14 9
А3	^3 4	^2 11	^6 7	^12 13
Потребности					70=70
βj

Для определения потенциалов решим следующую систему:

Положим α₁=0. Тогда β₁=2; α₂=3; β₂=1; β₃=5; α₃=1; β₄=11. Найденные потенциалы вносим в таблицу 5.9.

Вычисляем псевдостоимости для свободных клеток и проставляем их в левые верхние углы клеток. Выбираем свободную клетку, в которой 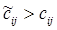; например, выберем клетку (1,4). Строим цикл пересчета, проходящий через эту клетку, и произведем по нему максимально допустимый сдвиг h = 10 (в отрицательных клетках наименьшей перевозкой является х₂₃=10). После сдвига клетка (2,3) становится свободной, а клетка (1,4) - базисной. Получаем новый опорный план, записанный в таблице 5.10.

Таблица 5.10

Пн По	В1	В2	В3	В4	Запасы	αi
А1	- ^2 5	^1^4	^0^7	+ ^6 10
А2	^5 17	^4 18	^3^8	^9^9
А3	+ ^8 7	^7 11	^6 17	- ^12 3
Потребности					70=70
βj

Вновь строим систему потенциалов, рассчитываем псевдостоимости, строим цикл пересчета, проходящий через клетку (3,1), делаем по нему максимально допустимый сдвиг величины h=3.

Таблица 5.11

Пн По	В1	В2	В3	В4	Запасы	αi
А1	^2 2	^1 4	^-4^7	^6
А2	^5 17	^4 18	^-1^8	^9 9
А3	^4	^2^11	^6 17	^8 1^2
Потребности					70=70
βj			-4

После сдвига получим опорный план, записанный в таблице 5.11. Построив систему потенциалов и рассчитав псевдостоимости, видим, что для всех свободных клеток . Поэтому опорный план оптимален.

Итак, оптимальный план имеет следующий вид: х₁₁=2; х₁₄=13; х₂₁=17; х₂₂=18; х₃₁=3; х₃₃=17.

При этом f_mln = 2•2 + 13•6 + 17•5 + 18•4 + 3•4 + 17•6 =353

Дата добавления: 2014-01-07