Потенциалы

Цена цикла пересчета

Ценой цикла пересчета называется разность между суммой стоимостей, стоящих в положительных клетках, и суммой стоимостей, стоящих в отрицательных клетках.

Например, цена цикла пересчета, указанного в таблице 5.5, равна (– 4).

Цена цикла пересчета - это приращение целевой функции при сдвиге h=1 по циклу пересчета.

Если, например, сделать единичный сдвиг по циклу пересчета таблицы 5.5, получится план перевозок, суммарная стоимость которого 430–4 = 426.

Имеет место, следующее утверждение: при сдвиге на величину h ≥ 0 по циклу пересчета, имеющему цену γ, приращение Δf целевой функции вычисляется по формуле

Δf = γ · h (5.5)

В справедливости формулы (5.5) можно убедиться и на примерах (таблицы 5.4, 5.5, 5.6). Из формулы (5.5) вытекает, что при положительном сдвиге по циклу пересчета с отрицательной ценой значение целевой функции уменьшается. Поэтому поиск оптимального плана перевозок сводится к выявлению циклов пересчета с отрицательной ценой и осуществлению максимально допустимых сдвигов по ним. А если циклов пересчета с отрицательной ценой не окажется?

Теорема: Опорный план перевозок, при котором все циклы пересчета имеют неотрицательные цены, оптимален.

Выявить цикл пересчета с отрицательной ценой при имеющемся опорном плане (или обнаружить, что такого цикла нет) можно было бы так: для каждой свободной клетки построим цикл пересчета и вычислим его цену. Однако в методе потенциалов для этой цели разработана менее трудоемкая процедура.

Пусть в транспортной задаче с пунктами отправления А₁, А₂,..., А_m и пунктами назначения В₁, В₂,..., В_n имеется некоторый опорный план перевозок. Сопоставим каждому пункту отправления A_i число α_i (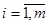), каждому пункту назначения В_j - число β_j (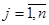) так, чтобы для каждой базисной клетки (p,q) выполнялось равенство

α_p + β_q = c_pq (5.6)

Числа α_i и β_j называются потенциалами пунктов отправления и назначения соответственно.

Для отыскания потенциалов нужно для каждой базисной клетки составить уравнение вида (5.6) и решить полученную систему m + n – 1 уравнений с m + n неизвестными. Такая система имеет бесконечно много решений. Чтобы получить конкретное решение, один из потенциалов полагают равным 0.

Найдем, например, систему потенциалов для опорного плана, данного в таблице 5.6. Составим систему уравнений:

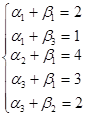
Положим α₁=0. Тогда β₁=2; β₃=1; α₂=2; α₃=1; β₂=1.
Дополним таблицу 5.6 столбцом с потенциалами α_i и строкой с потенциалами β_j, получим таблицу 5.7.

Таблица 5.7

Пн По	В1	В2	В3	Запасы	αi
А1	^2^2 0	^1^3	^1^1
А2	^4^4 60	^3^2	^3^5
А3	^3 3	^2 2 40	^2 6
Потребности				150=150
βj

Назовем псевдостоимостью перевозки единицы груза из пункта А_i в пункт В_j величину

Рассчитанные для таблицы 5.7 псевдостоимости помещены в левых верхних углах этой таблицы.

Потенциалы и псевдостоимости имеют любопытную экономическую интерпретацию. Предположим, что имеется перевозчик, который взимает с пункта А_i плату α_i за вывоз единицы груза, а с пункта В_j - плату β_j за ввоз единицы груза. Тогда псевдостоимость 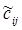– это та выручка, которую получает перевозчик за перевозку единицы груза из пункта А_i в пункт В_j. Полезно применить эту интерпретацию для лучшего понимания того условия оптимальности опорного плана, которое будет приведено ниже.

А пока докажем следуйте утверждение:

цена γ_ij цикла перерасчета, проходящего через свободную клетку (ij), выражается формулой:

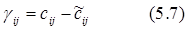
Для доказательства рассмотрим рисунок 5.1.

Рис. 5.1.

Клетка (ij) - единственная свободная клетка изображенного цикла пересчета. Цена γ_ij цикла пересчета, согласно определению, равна

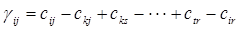
Так как для базисных клеток выполняются равенства (5.6), то
можно записать:

, что и требовалось доказать.

Из формулы (5.7) вытекает, что если для свободной клетки псевдостоимость больше стоимости, то через эту свободную клетку проходит цикл пересчета с отрицательной ценой. В частности, условие оптимальности опорного плана перевозок можно сформулировать так:

если, опорный план перевозок таков, что для всех свободных
клеток псевдостоимость не превосходит стоимости, то этот план
оптимален.

Например, опорный план перевозок таблицы 5.7 не является
оптимальным, так, как для клетки (2.2) псевдостоимость больше
стоимости. Цена, цикла пересчета, проходящего через эту клетку
отрицательна и равна 2–3=–1 (в этом можно лишний раз
убедиться, подсчитав цену, исходя из определения). Сделав максимально допустимый сдвиг величины h=40, получим таблицу 5.8.

Таблица 5.8

Пн По	В1	В2	В3	Запасы	αi
А1	^2 2 0	^0 3	^1 1
А2	^4 4 20	^2 2	^3 5
А3	^3 3	^1 2	^2 6
Потребности				150=150
βj

Построим систему потенциалов для таблицы 5.8. При небольшом навыке это можно сделать, не выписывая систему уравнений. Рассчитав затем псевдостоимости, видим, что для всех свободных клеток псевдостоимости не превосходят стоимостей. Следовательно, опорный план таблицы 5.8 оптимален.

f_min=40•1+20•4+40•2+50•3=350

Дата добавления: 2014-01-07