Переход от представления во временной области в частотную область. Структурные схемы многомерных систем управления. Управляемость, стабилизируемость, нормализуемость

Лекция 4

При анализе динамики линейных многомерных систем с постоянными параметрами можно использовать представление во временной области, т. е. в пространстве состояний

или же представление в области комплексной переменной s, т. е. в частотной области

(26)

В выражении (26) черта сверху обозначает преобразование Лапласа соответствующей функции времени; G(s), Ga(s) — матричные передаточные функции, связывающие управление и и возмущение d(s) с выходом y(s):

(27)

Отметим при этом, что представление в частотной области не содержит аналога вектора состояния х.

Поскольку одни методы синтеза систем управления проще реализуются во временной области, а другие — в частотной, разработчик должен уметь быстро переходить от одного представления к другому.

Переход от представления (24) — (25) к представлению (26) единствен, он осуществляется применением преобразования Лапласа к уравнениям (1) и (2) с нулевыми начальными условиями (х0 = 0):

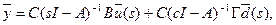(28)

откуда:

(29)

(30)

Для выполнения расчетов на ЭВМ по выражениям (28) — (30) имеются эффективные стандартные программы.

Обратный переход к временному представлению значительно сложнее. Это объясняется следующими причинами: 1) обратный переход не единствен, так как в общем случае представление в пространстве состояний содержит больше информации, чем просто передаточная функция; по одной и той же передаточной функции (28) можно построить целое семейство уравнений вида (24) — (25); 2) из всех возможных систем в пространстве состояний, соответствующих заданной передаточной функции (28), обычно выбирают минимальную реализацию, т. е. систему с наименьшей размерностью пространства состояний, хотя и в этом случае неединственность остается, так как есть много способов построения минимальной реализации. Приведем здесь один из наиболее эффективных алгоритмов построения минимальной реализации в случае различных действительных полюсов передаточной функции.

Дата добавления: 2014-01-07