Управляемость

Весьма существенным при анализе систем управления является понятие управляемости. Неформально система управляема, если найдется такое управление u (t), которое обеспечивает ее перевод из произвольного начального состояния х₀ в произвольное же состояние x_d за конечное время. Более строго определение управляемости может быть сформулировано следующим образом.

Система называется полностью управляемой, если из любого начального состояния x_о(t_о) она может быть переведена в любое наперед заданное состояние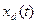с помощью некоторого управления u (t) за конечное время .

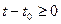Возможен случай частично управляемой системы, т. е. системы, имеющей подмножества начальных состояний, из которых достижение произвольного желаемого состояния за конечное время невозможно.

Из этого дескриптивного определения для конкретных классов систем можно получить конструктивные условия управляемости. Так, в случае постоянных матриц А и В система (1) — (2) будет полностью управляема тогда и только тогда, когда ранг матрицы управляемости Lc равен n, где

(60)

Нестрогий вывод этого условия может быть проделан с исполь­зованием аналитического выражения для решения системы (1) —(2):

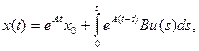(61)

где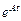может быть записана в виде

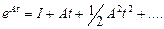(62)

Согласно теореме Гамильтона — Кэли е^Аt выражается в виде конечного ряда, или матричного полинома,

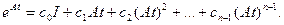(63)

Подставив (62) в (61), получим;

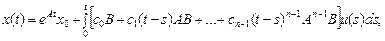(64)

или

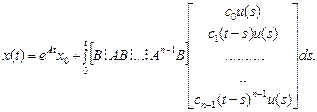(65)

Поскольку управляемость означает, что управление и влияет на все состояния х посредством интегрального члена в (65), ясно, что система будет управляемой тогда и только тогда, когда подынтегральное выражение в (65) обеспечивает такое влияние, т. е. когда ранг матрицы 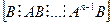равен п. Условие управляемости не по состояниям, а по выходам можно получить, умножив обе части уравнения (64) на С:

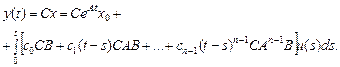(66)

Управляемость по выходам будет обеспечиваться в том случае, когда управление u(t) будет влиять на все I выходов у(0) т. е. выход у будет полностью управляемым тогда и только тогда, когда равен / ранг соответствующей матрицы управляемости

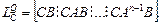(67)

Условие управляемости для случая линейной нестационарной системы в форме (3.2.1) с известными матричными функциями времени А, В состоит в том, что (п X п)-матрица A(t_o, t_f) невырожденная, т. е. det M(t_o, t_s) 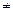0, где

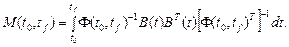(68)

Напомним, что Ф(t,tо)— фундаментальная матрица системы, т.е. решение матричного линейного однородного уравнения

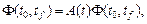
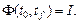(12)

Доказательство необходимости и достаточности этого условия для полной управляемости почти очевидно, поэтому оно здесь не приводится. Укажем только, что подынтегральное выражение в (12) положительно полуопределено, и для управляемости достаточно, чтобы в каждый момент времени t, 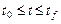подынтегральное выражение было не вырождено. Рассмотрим примеры, иллюстрирующие изложенные положения.

Стабилизируемость Значительно более слабым, чем управляемость, является свойство стабилизируемости. Оно заключается в том, что воздействием регулятора в цепи обратной свзязи все неустойчивые моды или собственные векторы управляемой системы могут быть сделаны устойчивыми, т. е. все положительные вещественные части собственных чисел могут быть сделаны отрицательными. Ясно, что устойчивая система, т. е. такая система у которой все собственные числа имеют отрицательные вещественные части, стабилизируема тривиальным образом (без регулятора). Кроме того, понятно, что всякая управляемая система стабилизируема, вполне управляемого объекта и не всегда для объекта, таковым не являющимся. Если управляемый процесс стабилизируем, а неуправляемые собственные значения (моды) имеют достаточно большие по модулю отрицательные действительные части, все еще возможно построить эффективную систему управления Однако, если управляемый процесс не является даже стабилизируемым, управление им невозможно.

Дата добавления: 2014-01-07