Структурные схемы многомерных систем управления

Теперь, когда в нашем распоряжении имеется достаточно простой аппарат перехода от временного представления линейных многомерных систем с постоянными коэффициентами к частотному их представлению и обратно, займемся анализом много­мерных систем управления с обратными связями. В начале рас­смотрим простую многомерную структурную схему, показанную на рис. 3. В частотной области выход определяется управляющими и возмущающими воздействиями согласно выражению

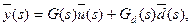(45)

где G(s), Gd(s) — матричные передаточные функции системы по управлению и по возмущению, определенные в (27), причем элементы этих матриц задаются выражением

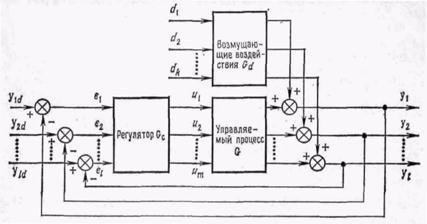
Рис. 3. Блок-схема многомерной системы регулирования

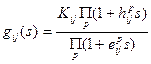(46)

где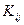— коэффициент усиления, 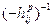— нули передаточной функции, 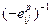— полюса передаточной функции. Эта же самая структурная схема (рис. 3) справедлива и для временного представления, однако при этом G и 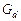имеют смысл некоторых интегральных операторов. Так, для линейной системы, задаваемой (1), при нулевых начальных условиях (хо = 0) G задает линейную форму (L, w), где L — линейный оператор, a w — некоторая функция, по правилу

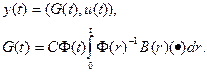(48)

Такое выражение G(t) получается непосредственно из решения системы (1) с соответствующими начальными условиями

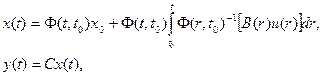(49)

где, как и раньше, квадратная (nxn) -матрица 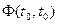является фундаментальной матрицей рассматриваемой системы, т. е. решением однородного матричного уравнения ,

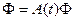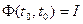
На структурной схеме рис. 3 показан также многомерный регулятор Gc. Матрица Gc может быть произвольной, однако на практике чаще встречается диагональный случай

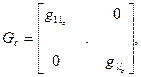(50)

при этом элементы g_ii, соответствующие одноконтурным (одномерным) регуляторам, как правило, задают ПИД-закон в частотной области:

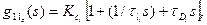i = 1, 2,..., l. (51)

или во временной области

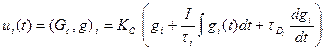(52)

Здесь ошибка, или рассогласование, определяется по выражению

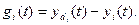(53)

Таким образом, структурные схемы, подобные той, которая изображена на рис. 3, представляют замкнутые линейные системы регулирования как во временной, так и в частотной области.

Операторное уравнение замкнутой системы получается подстановкой в уравнение разомкнутой системы

(54)

выражения для ошибки

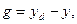(55)

где 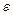— l -мерный вектор отклонений фактического выхода от заданного y_d, d — р -мерный вектор возмущений. Подстановка дает

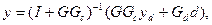(56)

или после упрощения

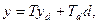(57)

где Т и T_d — передаточные функции замкнутой системы по управлению и возмущению соответственно:

(58)

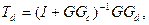(59)

Прежде чем переходить к рассмотрению основных методов синтеза регуляторов, введем некоторые основные концепции, связанные с поведением управляемых систем.

Дата добавления: 2014-01-07