Химический потенциал

Для системы, состоящей из одного вещества, справедливо:

, (61)

Любая экстенсивная функция состояния является функцией количества вещества в системе.

Поэтому, если система состоит из нескольких компонентов, то

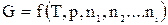, (62)

где n_i – число молей i -го компонента. Продифференцируем (62) по n_i

p, Т, n_j≠i=const

(63)

Величину Гиббс назвал химическим потенциалом и обозначил μ _i Его ещё называют парциальной мольной энергией Гиббса (парциальная термодинамическая функция Гиббса)

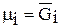
Можно дать следующее определение химического потенциала:

Это изменение энергии Гиббса однородной многокомпонентной системы при добавлении к ней 1 моля данного компонента при постоянных давлении, температуре и составе системы (т.е. добавление должно происходить при бесконечно больших количествах всех компонентов, чтобы состав системы не изменился).

Химический потенциал в отличие от, например, энергии Гиббса G, – интенсивная величина, т.е. он не зависит от массы системы, а зависит от природы системы и ее состава, температуры и давления. Вообще говоря, m_i зависит от силы химического взаимодействия данного компонента с другими компонентами: чем это взаимодействие сильнее, тем меньше m_i. Сила взаимодействия зависит от концентрации компонента, причем, чем меньше концентрация i-ого компонента, тем взаимодействие сильнее, и тем меньше m_i. Вещество стремится переходить из состояния, где его m больше, в состояние, где его m меньше (т.е. туда, где сильнее взаимодействие данного компонента с другими компонентами).

Любая энергетическая характеристика есть произведение интенсивного фактора на экстенсивный. В нашем случае μ_i – интенсивный параметр, а n_i – экстенсивный. Тогда:

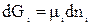при T, p = const. (64)

Введение некоторого количества dn_i молей i–го компонента при постоянном количестве других компонентов и постоянных Т и р будет увеличивать значение энергии Гиббса на величину . Аналогичные изменения будут вызваны прибавлением других компонентов. Общее изменение энергии Гиббса системы при добалении в нее нескольких компонентов равно:

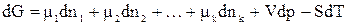, (65)

или, в общем случае,

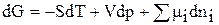(66)

Это уравнение получило название фундаментального уравнения Гиббса.

Проинтегрируем соотношение (64) при постоянном составе системы (т.е. когда m_i = const):

,

получим:

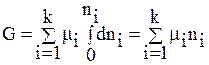(67)

Соотношение (67) иногда называется уравнением Гиббса-Дюгема (чаще данное уравнение записывают таким образом:

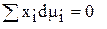, где x_i - молярная доля i-ого компонента.)

При р, Т = const для химической реакции верно:

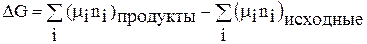. (68)

Расчёт химического потенциала идеального газа:

Если у нас есть один чистый компонент, то его химический потенциал m равен молярной энергии Гиббса :

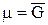. Но

(69)

(Здесь 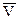и 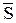– молярный объем и молярная энтропия вещества), тогда получим:

(70)

Пусть идеальный газ находится при Т = const, тогда

dT = 0 и

dm = 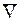dp (71)

Проинтегрируем выражение (71) от р⁰ = 1 атм до любого р и, соответственно, от m⁰ до m; получим:

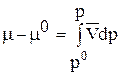; . (72)

Но для идеального газа выполняется закон Менделеева–Клапейрона, который для 1 моль газа имеет вид:

р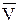= RT, отсюда 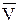= 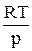. (73)

Тогда получим:

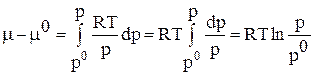(74)

Если р⁰ = 1 а тм, то

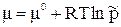(75)

В уравнении (75) р – не само давление, а безразмерная величина, численно равная давлению, выраженному в атмосферах ().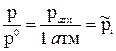

m⁰ – стандартный химический потенциал, т.е. химический потенциал при стандартном давлении р⁰ = 1 атм;

Если же имеется смесь газов, то для любого i-ого компонента смеси.

m_i = m⁰_i + RT ln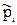 (76)

Здесь 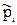– безразмерная величина, численно равная парциальному давлению i-ого компонента смеси (т.е. той части от общего давления, которая приходится на i-ый компонент), выраженному в атмосферах ().

Так как 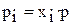, где 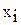– мольная доля i–го газа в смеси, p – общее давление в системе, то

.

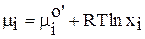Дата добавления: 2014-01-07