Обчислення площ плоских фігур у декартовій системі координат

Обчислення площ плоских фігур

Застосування інтегрального числення

Розділ 10

Якщо на відрізку 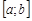задана неперервна функція , то, згідно з геометричною інтерпретацією визначеного інтеграла, площа криволінійної трапеції, обмеженої кривою 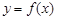, прямими 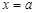, 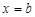та віссю 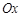(рис.1), обчислюється згідно з формулою:

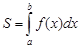. (1.1)

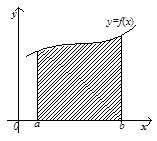
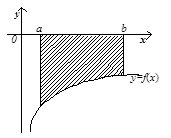
Рис.1 Рис.2

Криволінійні трапеції (рис.1 – при 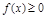, рис.2 – при )

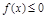Якщо на відрізку 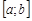функція 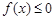(рис.2), то криволінійна трапеція буде розміщена у нижній півплощині і відповідний визначений інтеграл буде від’ємним. Оскільки площа фігури є величиною невід’ємною, то її можна обчислити згідно з формулою

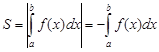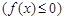, . (1.2)

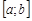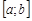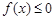Якщо на відрізку функція декілька разів змінює знак (рис.3), то інтеграл на відрізку слід розбити на суму інтегралів по часткових відрізках – відрізках знакосталості функції. Інтеграл буде додатнім на тих відрізках, на яких та від'ємним там, де . Інтеграл на відрізку 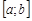дає різницю площ фігур, що лежать вище та нижче осі .

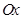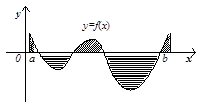
Рис.3. Геометрична інтерпретація інтеграла від

знакозмінної функції

Щоб знайти суму площ без врахування розташування відносно осі 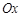, треба знайти суму абсолютних величин інтегралів на відрізках знакосталості функції або обчислити інтеграл від абсолютної величини функції, тобто (рис.4)

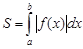. (1.3)

Рис.4. Геометрична інтерпретація інтеграла

від модуля функції

Приклад 1.1. Обчислити площу фігури, обмеженої лініями та 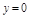на проміжку .

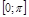á Згідно з формулою (1.1) для невід'ємної на 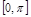функції матимемо

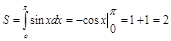(кв.од.).

Якщо треба обчислити площу фігури, розміщеної між лініями , 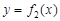та прямими 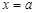, 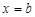(на відрізку 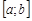) (рис.5), то формула площі запишеться

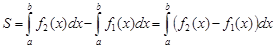. (1.4)

Рис.5.

Приклад 1.2. Обчислити площу фігури, обмеженої параболами ; .

á Розв’язуючи систему рівнянь 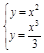, знаходимо абсциси точок перетину: ; .

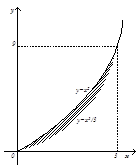Вважаючи 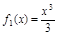, 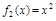на підставі формули (1.4) отримаємо

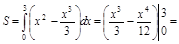
(кв.од.).

Дата добавления: 2014-01-07