Подобные преобразования для двух нагоняющих годографов

Пусть мы имеем годограф с источником в точке r = r ₀₁ (рис.30) Преобразуем его координаты по формулам (42)

R = r ₁ / r _{0 1,} T = t / r _{0 1} ^{1 - m}

Получим уравнение:

T = R ^{m- 1} T (R)

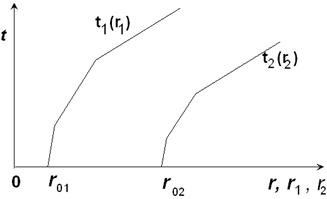
Рис. 4.6.

Этот годограф численно совпадает с годографом, источник которого расположен в точке r ₀ = 1 (единичный годограф). Используя полученный годограф и преобразования подобия можно вычислить годограф с источником в любой точке поверхности среды r 0 = r 02. Это делается по формулам (42) при значении r ₀ =r ₀₂

r ₂ = r ₀₂ R = (r _{02 /} r ₀₁ ) r ₁

(46)

t ₂ = r ₀₂ ^{m- 1} T = (r ₀₂ /r ₀₁ ) ^{1 - m} t ₁

Так как в формуле скорости (25) функция ψ(φ) -произвольная функция полярного угла, то она может иметь точку разрыва, φ= φ* где значение функции изменяется скачком, при этом двухмерная скоростная функция v = r ^m ψ (φ) будет содержать прямую наклонную линию разрыва φ = φ * -границу раздела. Тогда, на поверхности среды мы зарегистрируем годограф состоящий из трёх ветвей - прямой рефрагированной волны t ^p, отражённой волны t ⁰,

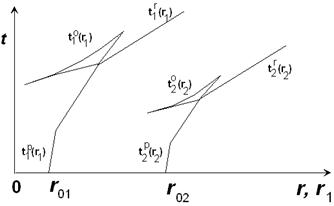
Рис. 4.7.

преломлённо-рефрагированной волны t ^r (рис.31).

4.9.3 Подобие годографов отражённых волн.

Для трёх ветвей годографа будут вернысоотношения подобия (35). Для годографовотражённой волны от границы φ = φ * на поверхности среды φ= 0 t ₁ ^o(r 1 ) и t ₂ ^o(r 2 ) (рис.7) подобны друг другу. Их координаты будут относиться:

r ₂ /r ₁ = r ₀₂ /r ₀₁, t ₂ ^o/ t ₁ ^o = (r ₀₂ / r ₀₁ ) ^{1 - m},

Рассмотренные выше преобразования (35) переводят правую ветвь годографа r 1 в правую же ветвь годографа r 2 или левую в левую, то - есть мы сформулировали соотношения подобия для нагоняющих годографов.

.

4.9.4 Преобразования для двух встречных годографов.

В рассматриваемых средах существуют нелинейные преобразования для двух встречных годографов, которые переводят прямой годограф в обратный и наоборот. Рассмотрим два встречных годографа - прямой t ₁ (r ₁ ) с источником в точке r ₀₁ и обратный t ₂ (r ₂ ) с источником в точке r ₀₂, заданные на отрезке [ r ₀₁ ,r ₀₂]. Годографы увязаны во взаимных точках: t ₁ (r ₀₂ ) = t ₂ (r ₀₁ ).

Рассмотрим произвольную точку прямого годографа t ₁, r ₁ (рис.32). Представим себе, что в этой точке r ₁ располагается источник r ₀ некоторого годографа t (r). Очевидно, по принципу взаимности – t (r ₀₁ ) = t ₁ (r ₀ ). Годограф t (r) - это нагоняемый годограф для t ₂ (r ₂ ), и следовательно, они подобны. Точки годографа t (r) можно преобразовать в точки годографа t ₂ (r ₂ ), используя формулу преобразования (35). Запишем эти преобразования для годографа t(r). Используем формулы для нагоняющих годографов, получим.

r ₂ =(r ₀₂ / r ₀ )r,

t ₂ = (r _{02 /} r ₀ ) ^{1 - m} t.

Подставим в эту формулу координаты одной точки годографа t (r) а именно [ t, r ₀₁ ]

r ₂ =(r ₀₂ / r ₀ ) r ₀₁ ,→

t ₂ = (r _{02 /} r ₀ ) ^{1 - m} t.

По принципу взаимности верно t(r ₀₁ ) = t ₁ (r ₁ ), причем r ₀₌ r _1.

Тогда:

r ₂ = (r ₀₂ /r ₁ ) r ₀₁

(47)

t ₂ = (r ₀₂ / r ₁ ) ^{1 -m} t _1,

или

Мы получили точку (t ₂, r ₂ ) на годографе t ₂ (r₂), отвечающую произвольной точке (t ₁, r ₁ ) годографа t ₁ (r ₁ ) или образ точки (r ₁, t ₁ ) на годографе t ₂.

Рис. 4.8.

Эти нелинейные преобразования непрерывно отображают прямой годограф в обратный и наоборот. Теперь рассмотрим точки источников (r ₀₁, 0 ) и(r ₀₂, 0). При преобразованиях (47) они переходят друг в друга:

r ₂ = (r ₀₁ / r ₀₁ ) r ₀₂ = r _02,

t ₂ = (r ₀₂ / r ₀₁ ) ^{1 – m} t ₁ = 0.

Взаимные точки также отображаются друг в друга:

(r ₁ = r ₀₂, t ₁ = T) → (r ₂ = r ₀₁, t ₂ = T),

так как

r ₂ = (r ₀₂ / r ₀₂ ) r ₀₁ = r ₀₁,

t ₂ = (r ₀₂ / r ₀₂ ) ^{1 - m} T = T.

Таким образом, поля времён, годографы и лучи в среде, где скорость волн однородная функция, образуют группу подобных друг другу лучей. Источники подобных полей времён, годографов, семейств лучей лежат на одной радиальной прямой j = const.

4.10 Преобразование уравнения поля времен для случая однородной функции произвольной степени V = r ^m y (j) к полю времен для одномерно-неоднородной среды.

Среда, где скорость волн - есть однородная функция двух координат - это двухмерно неоднородная среда или двухмерная градиентная среда. Скорость волн зависит от двух координат разреза. Однако для такой среды прямые и обратные задачи могут быть сведены к одномерным задачам.

В уравнении поля времён

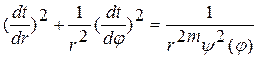(48)

Преобразуем переменные по формулам:

r = r ^{1 - m},

a = ½1 -m ½ j, (49)

t = ½1- m ½ t,

Получим:

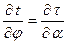
Уравнение (36) перепишем в виде:

или

(50)

Мы получили уравнение поля времён в полярных координатах для среды, где скорость волн есть функция только полярного угла, то есть, одномерное уравнение. Это позволяет прямые и обратные задачи для таких сред свести к одномерным, а это значит упростить их в очень значительной степени. Итак, поля времён и годографы для среды со скоростью

v = r ^m y(j)

с помощью преобразований координат вида:

r = r ^{1- m}

a = ç 1-m ç j

t = ç 1-m ç t

трансформируются в поля времён и годографы для среды, где скорость зависит только от полярного угла:

x = x (a) =y (j / ç1 -m ç ).

Однако для случая m= 1, то есть для однородной скоростной функции первой степени преобразования (46)не имеют смысла, так как:

r = r ⁰ = 1,

a = 0,

t = 0.

Это особая точка. Рассмотрим этот случай отдельно.

4.11. Преобразования уравнения поля времен для случая m=1 однородной скоростной функции к уравнению поля времен для вертикально-неоднородной среды.

Дата добавления: 2014-01-07