Вычисление среднего годографа, отвечающего аппроксимирующей функции

Обратная кинематическая задача сейсмики для среды, где скорость волн - однородная функция произвольной степени.

Обратная кинематическая задача сейсмики для среды, где скорость волн - однородная функция первой степени.

Обратные задачи для среды со скоростью v = ry(j) также могут быть решены способами, известными для вертикально - неоднородных сред. Например, способом Герглотца - Вихерта - Чибисова или способом Кондратьева. Однако если для вертикально-неоднородной среды, чтобы вычислить скоростную функцию v = v(z) достаточно задать один годограф t = t(x), то для среды со скоростью v= r y (j) для этого необходимы два встречных годографа t ₁ (x ₁ ) и t ₂ (x ₂ ),увязанные во взаимных точках (пара встречных или два нагоняющих или две ветви годографов из одного пункта взрыва. Пусть заданы два встречных годографа на поверхности среды t₁(x₁) и t₂(x₂) на интервале [ х₀₁, х₀₂ ], где х ₀₁ и х ₀₂ - декартовы координаты источников (х - значение пикетов профиля в метрах или километрах (рис.35)

Найдём по эти данным распределение скорости в среде в виде функции v=ry(j).

Мы предполагаем, что начало полярной системы координат находится в неизвестной

Рис.4.11

точке профиля справа или слева от расстановки, то есть будем предполагать,

что на поверхности среды при j=0

r=│x+C │.

Если скорость в среде – однородная функция, то прямой годограф может быть

преобразован в обратный в полярной системе координат по формулам (47).

r ₂ = (r ₀₁ / r ₁ ) r _02,

t ₂ = (r ₀₂ / r ₁ ) ^{1- m} t _1.

Запишем эти равенства в координатах профиля (в декартовой системе координат).

x ₂ + C = (x ₀₁ + C) (x ₀₂ + C) / (x ₁ + C),

t₂ = (x ₀₂ +C) ^{1- m} t ₁ / (x ₁ + C) ^{1- m} (54)

при m = 1 второе равенство запишется в виде:

t ₂ = t _1.

Времена в точках, которые преобразуются друг в друга, равны. Если на заданных годографах (рис.30) провести горизонтальную черту, то получим значения x ₁и x ₂ для двух таких точек. Так как x ₀₁и x ₀₂ известны, то значение С можнонайти из первого из уравнений (54).

x ₂ + C = (x ₀₁ + C) (x ₀₂ + C)/(x ₁ + C) =>

(x ₂ +C) (x ₁ +C) =(x ₀₁ +C) (x ₀₂ +C) =>

x ₁ x ₂ + C x ₂ + C x ₁ + C ² = x ₀₁ x ₀₂ + C x ₀₂ +C x ₀₁ +C ² =>

C x ₁ + C x ₂ – C x ₀₂ – C x ₀₁ = x ₀₁ x ₀₂ - x ₁ x ₂ =>

C = (x ₀₁ x ₀₂ - x ₁ x ₂ ) / [(x ₁ + x₂) - (x ₀₁ + x ₀₂)] (55)

Значение С определяется как разность произведений, делённая на разность сумм источников и приёмников..Если бы реальная среда в точности соответствовала некоторой функции v =ry(j), то для любых двух точек на заданных годографах получилось бы одинаковое значение С. Однако реальная среда сложнее. Определим С для нескольких пар точек, времена которых равны, и потом вычислим С как среднеарифметическое значение:

_n

С = å C_i /n(n = 7 ¸10)

ⁱ⁼¹

Чем меньше разброс значений С, тем меньше реальная среда отличается от аппроксимирующей функции. Затем перейдём от декартовых координат к полярным по формулам (рис.36)

r = ê x + C ê

r ₀₁ = ê x ₀₁ + C ê

r ₀₂ = ê x ₀₂ + C ê.

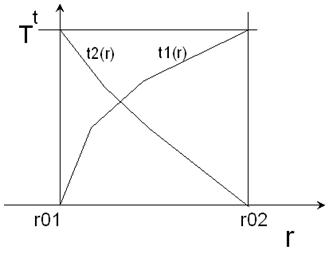
Рис.4.12.

После этого наблюдённые годографы преобразуем в годографы, отвечающие вертикально-неоднородной среде со скоростью v=y(z). Для этого построим их в полулогарифмическом масштабе (рис.37).

x = ln r, x ₀₁ = ln r _01,

T = t, x ₀₂ = ln r _02.

Рис.4.13.

Построенные в таких координатах годографы T₁(x₁), T₂(x₂) должны быть выпуклыми и идентичными друг другу. То есть, если совместить их пункты взрыва, то они должны совпасть. Однако для реальных сред они будут отличаться друг от друга. Совместим их пункты взрыва и осредним годографы. Это означает, что если взять времена годографов в точках, расположенных на одинаковом расстоянии от источников, то нужно вычислить среднее из этих времён.

T(x ₁ ) = (1/2) (T ₁(x ₀₁ + ∆x) + T ₂(x ₀₂ - ∆x))

пусть

0 ≤ ∆x ≤ x ₀₂ - x _{0 1},

x ₁ = x ₀₁ + ∆x

∆x = x ₁ - x ₀₁

Будем считать, что вычисленный таким образом T (x ₁) в точности соответствует некоторой вертикально-неоднородной среде, где скорость есть неизвестная функция глубины v=y(z).. Найти её можно теперь известными способами Герглотца - Вихерта - Чибисова или, приближённо, способом Кондратьева. В результате вычислим кривую y(j) =v(z) (км/сили м/с). Значения j = z будутполучены в радианах.

Как построить разрез? Находим положение начала полярной системы координат однородной скоростной функции. Пусть С < - х₀₂. С - отрицательна. Тогда отрезок, равный С нужно отложить влево от точки х =0. Чтобы ограничить приближённо область, где скорость описывается формулой v = r y(j), необходимо провести граничный луч, соединяющий точки источников. Заменим его дугой окружности, для этого через середину отрезка [ x₀₁,x₀₂ ] проведем перпендикуляр к прямой j = j_max. Получим точку М, и затем через три точки х ₀₁, х ₀₂и М проведём дугу окружности. Внутри этой окружности скорость можно найти по формуле:

v = ((X ₁ +C)² + Z ²) ^1/2 y (arctg (Z / ê X+C ê).

Возьмём любую точку (x^*,z^*) внутри этой окружности в декартовых координатах,тогда

r^* = ((x^* +C) ²+ z ^*2) ^1/2,

j ^* = arctg (z ^*/(x ^* + C)).

Значение y(j^*) снимем с графика y(j). Вычислив несколько таких значений, можно построить изолинии скорости внутри граничного луча. Этим способом можно вычислить поле скорости на калькуляторе. Однородная функция первой степени - это частный случай однородных функций. Скорость всегда возрастает по падению границы раздела и по радиальной координате изменяется линейно.

4.3.1 Постановка задачи

Пусть заданы два встречных годографа первых волн: t ₁ (x ₁)с источником в точке x ₀₁и t ₂ (x ₂)с источником в точке x ₀₂, увязанные во взаимных точках (рис.38). Предполагается, что скоростное распределение может быть аппроксимировано функцией вида: v = r^my(j). Значения радиальных координат r,

нам неизвестны. Также как и выше,

Рис.4.14..

предполагаем, что начало полярной системы координат находится в неизвестной точке профиля слева или справа от расстановки. Отсюда на поверхности среды при φ = 0, имеем

r = │x +C│,

r ₀₁ = │x ₀₁ +C│,

r ₀₂ = │x ₀₂ +C│,

где С - неизвестная константа. Значения полярных координат разреза

определяются по формулам:

Неизвестными, таким образом, в этой задаче являются параметры скоростного закона m и C, а также значения функции y (j). Необходимо положить ограничения на искомые параметры. Практика показывает, что достаточно искать значения m в диапазоне -3 ≤ m ≤ 3. Ограничения на C мы получим, решив систему неравенств:

Так как r =0 не может находиться внутри интервала х ₀₁, х ₀₂

r _{01 >} 0, или r _{01 <} 0,

r _{02 >} 0, r _{02 <} 0.

Отсюда получим С > - х ₀₁, С < -х ₀₂ (рис. 39)

.

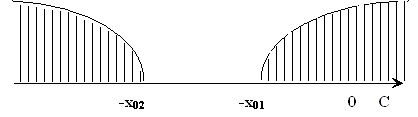
Рис.4.15. Область определения С.

Известно, что в случае, когда скорость в среде есть функция вида (25) прямой t₁(x₁) и обратный t₂(x₂) годографы связаны между собой формулами:

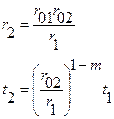
или в декартовой системе координат:

Возьмём произвольные значения m и C и преобразуем обратный годограф в прямой. Для этого выберем произвольную точку x ₁ на прямом годографе t ₁(x ₁). Соответствующая этой точке точка х ₂ на годографе t ₂(x ₂) (х ₂ -образ точки x ₁) определяется по формулам:

Возьмём время t ₂ в найденной точке х ₂и пересчитаем его обратно в точку x ₁ по формуле:

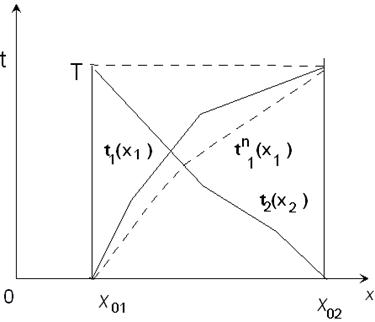
Рис.4.16..

для точки t ₁(r ₀₂) = T другого конца годографа t ₁(r ₁), получим:

Таким образом, преобразованный прямой годограф t ₁ ⁿ будет отличаться от

наблюдённого прямого, так как показано на рис.40. Пусть на годографе t ₁(х ₁),

имеется n точек, тогда cреднее квадратическое отклонение прямого наблюдённого годографа от преобразованного прямого при произвольных значения параметров может быть записано в виде:

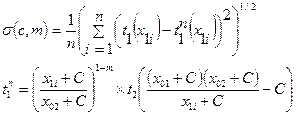
σ(c,m) - функция двух переменных, параметров m и C. Необходимо найти такие значения m и C, при которых данное среднеквадратическое отклонение минимально: σ(c,m)= min, то есть необходимо найти координаты m и C точки минимума. Значения этих координат будем считать параметрами искомой скоростной функции.

4.3.2. Поиск минимума функции нескольких переменных .

Минимум функции нескольких переменных может быть найден численными методами на компьютере. Существуют алгоритмы такого поиска. Например, известный алгоритм градиентного спуска. Рассмотрим метод прямого поиска минимума функции нескольких переменных. Существует стандартная процедура- DIRECTSEARCH такого поиска. Как построен алгоритм?

Рассмотрим рис. 4.17

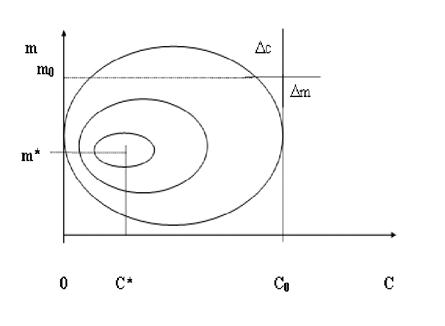
Рис. 4.17.

На рис. 4.17. изображены изолинии функции σ(c,m) =const. Выберем произвольную начальную точку m₀, c₀. У нас есть алгоритм (формула), позволяющая вычислить функцию σ(c,m). Вычислим значение этой функции в начальной точке. Зададим некоторый шаг D c, D m и вычислим значения σ (c,m) ещё в четырёх точках: σ(c₀,m₀+ D m), σ(c₀,m₀ -D m), σ(c₀+ D c,m₀), σ(c₀ - D c,m₀), то есть, определим значения функции σ для некоторой расстановки типа крест. Затем выберем из этих значений минимальное. В данном случае это будет σ(c₀, m₀ - D c) и переместим центр расстановки в эту точку. Далее процедура вычислений повторяется. Крест будет ползти в сторону минимума. Если минимальное значение получается в центральной точке креста - шаг дробится. Алгоритм процедуры прямого поиска становится понятнее, если рассмотреть обращение к процедуре DIRECTSEARCH.

DIRECTSEARCH (N(число переменных), RHO(параметр уменьшения шага поиска), DL(наименьший шаг), MF(процедура вычисления значений функции), M(максимальное число вычислений функции), MX(начальный шаг), D(координаты минимума), MFS(значение функции в точке минимума), P₁ (логическая переменная, если P₁ - истинно, то найден минимум, если P₁ - ложно выход из процедуры осуществлён при достижении количества вычислений функции больше значения M).

Структура линий уровня функции σ нам не известна - функция может содержать несколько минимумов. Эта проблема решается следующим образом: задаём несколько значений начальных точек, в нашем случае - 4. Вычислим координаты четырёх точек минимума. А затем выберем из них ту, в которой значение σ наименьшее.

В рассмотренном случае, мы считаем функцию σ функцией двух переменных. Однако, как мы сейчас увидим, эта задача может быть сведена к поиску функции одной переменной. Действительно, если для пары годографов, задано некоторое произвольное значение параметра С, то оптимальное значение m степени однородной аппроксимирующей функции может быть вычислено. Возьмём произвольную точку прямого годографа х₁, t₁. Зададим некоторое значение С. Соответствующая точка х ₂ (образ точки х ₁), при заданном значении С может быть найдена по формуле:

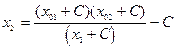
Возьмём значение t ₂ в точке x ₂. Известно, что:

отсюда:

m = 1 - A

Взяв несколько точек прямого годографа вычислим 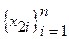, для каждой пары точек можно вычислить своё значение m_i, а затем вычислить среднеарифметическое значение:

После этого для заданного С и вычисленного m необходимо найти среднеквадратическое отклонение прямого наблюдённого от преобразованного прямого σ (С, m). В этом случае σ является функцией только одного переменного С. Таким образом можно вести поиск минимума функции σ (С) передвигаясь только по одной координате С. Это уменьшает время счёта примерно в пять раз. Точность вычислений при этом не теряется. Итак, минимум найден. Пусть это будут значения m^*, C^*.

Трансформируем годографы к полярным координатам по формулам:

и преобразуем обратный годограф в прямой по формулам:

t₁ⁿ- преобразованный прямой годограф, r - произвольная точка прямого годографа. Найдём средний годограф между прямым наблюдённым и прямым преобразованным годографами по формуле:

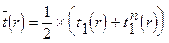
Будем считать, что этот годограф точно соответствует некоторой искомой скоростной функции вида:

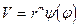(56)

среднеквадратическое отклонение:

характеризует степень отклонения реальной среды от аппроксимирующей функции - погрешность аппроксимации.

Дата добавления: 2014-01-07