Решение однородных уравнений

Рассмотрим линейное однородное дифференциальное уравнение.

С целью отыскания каких-нибудь частных решений линейного однородного дифференциального уравнения (79), постараемся выяснить, какие функции могли бы обратить это уравнение в тождество. Для этого нужно, чтобы при подстановке решения в левую часть уравнения (79) там оказались подобные члены, которые в сумме могли бы дать ноль. Такой функцией, которая подобна со всеми своими производными в смысле элементарной алгебры (т.е. отличается от производных лишь постоянным множителем), является функция у = e^kx (где k = const).

Итак, попытаемся удовлетворить линейному однородному дифференциальному уравнению (79), полагая: у = e^kx (где k = const). Откуда,

у^/ = k e^kx

y^|| = k² e^kx.,

……………

Тогда, подставив полученные выражения производных в уравнение (79), получаем:

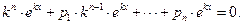
Разделив обе части последнего уравнения на 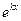(), будем иметь:

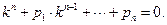(80)

Таким образом, функция у = e^kx (где k = const) является решением уравнения (79) тогда и только тогда, когда константа k является корнем уравнения (80), которое называется характеристическим уравнением.

Из курса высшей алгебры известно, что многочлен с действительными коэффициентами степени n имеет ровно n корней, которые могут быть действительными или комплексными числами, причём, комплексные корни возникают только сопряжёнными парами. Рассмотрим все возможные случаи появления корней.

1). Пусть уравнение (80) имеет n действительных и различных корней, тогда функции - будут частными решениями однородного уравнения (79). Покажем, что эти частные решения – линейно независимые функции, т. е. могут составить фундаментальную систему решений ЛОДУ (79). Для этого составим определитель Вронского для этих функций и покажем, что он отличен от нуля на всей числовой оси.

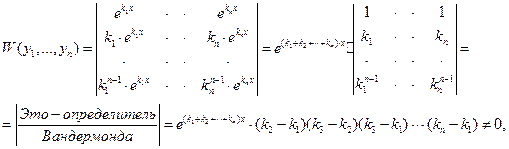
так как все корни – различные. Следовательно, общее решение ЛОДУ имеет вид: (81)

2). Случай действительных кратных корней (ограничимся рассмотрением ЛОДУ только второго порядка).

В этом случае уравнение (80) является квадратным уравнением и имеет два равных действительных корня.

Итак корни k₁ и k₂ действительные и равные (т.е. k₁ = k₂=К)

Характеристическое уравнение имеет вид: 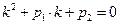, его дискриминант равен нулю и корни имеют вид: 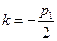. Но две одинаковые функции не могут составить общего решения однородного уравнения, так как всегда линейно зависимы. Для нахождения второго, линейно независимого по отношению к первому решению, используем формулу Лиувиля – Остроградского:

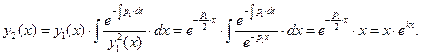
Общее решение однородного уравнения принимает вид: 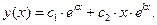(82) Корню кратности, например, три будут соответствовать три линейно независимые частные решения вида: 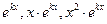и т. д.

3) корни k₁ и k₂ - комплексные сопряженные (тогда k₁ и k₂ имеют вид: , где α и β действительные константы, 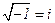). Тогда общее решение уравнения имеет вид:

y = e^αx (C₁cosβx + C₂sinβx) (83)

Пример. Найти общеерешение следующих уравнений:

а) у^// + 3у^/ +2у = 0 г) у^// + 4у^/ + 13у = 0

б) у^// - 3у^/ = 0 д) у^// +5у = 0

в) у^// - 4у^/ + 4у = 0

Решение. Все данные уравнения представляют собой линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

а) у^// +3у^/ +2у = 0

Составляем соответствующие характеристическое уравнение:

k² + 3k + 2 = 0

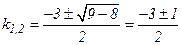; k₁ = -2, k₂ = -1.

Итак, корни k₁ = -2, k₂ = -1 действительные и различные, а значит общее решение уравнения определяется формулой (81):

у = С₁ е^ох + С₂ е^3х = С₁ е^о + С₂ е^3х = С₁ 1 + С₂ е^3х = С₁ + С₂ е^3х.

в) у^// - 4у^/ + 4у = 0.

Составим и решим соответствующее характеристическое уравнение:

k² - 4k + 4 = 0;

(k – 2)² = 0;

k₁ - k₂ = 2;

Итак, корни k₁ = k₂ = 2 действительные, равные, а значит общее решение уравнения определяется формулой (82): у = С₁ е^2х + С₂ е^2х х.

г) у^// + 4у^/ + 13у= 0.

Составим и решим соответствующее характеристическое уравнение:

k² + 4k + 13 = 0;

D = 4² – 4 · 13 = -36, тогда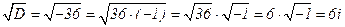

.

Итак, имеем пару комплексных сопряженных корней k₁ = -2 + 3i и k₂ = -2 - 3i (тогда α = -2; β = 3), а значит общее решение уравнения определяется формулой (83):

y = e^-2x (C₁cos3x + C₂sin3x)

д) у^// + 5у = 0

Составим и решим соответствующее характеристическое уравнение:

k² + 5 = 0;

k² = -5;

.

Итак, имеем пару комплексных сопряженных корней и 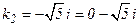(тогда ), а значит общее решение уравнения (77) определяется формулой (83):

.

Дата добавления: 2014-01-07