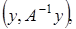КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 6-7. Линейные операторы. Пространства линейных операторов. Обратные операторы. Сопряженные операторы
|
|
|
|
Изложены основы теории линейных операторов. Приведены теоремы Банаха об обратном операторе и о замкнутом графике. Рассмотрены виды сходимости в пространстве линейных операторов, а также теоремы о продолжении линейного оператора по непрерывности. Большое внимание уделено обратным и непрерывно обратимым операторам, сопряженным операторам и основам теории нормально-разрешимых операторов.
Линейные операторы. Оператор  где
где 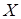 ,
, 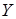 – банаховы пространства, называется линейным, если: 1) область определения оператора
– банаховы пространства, называется линейным, если: 1) область определения оператора 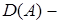 линейное многообразие; 2)
линейное многообразие; 2)  для любых
для любых  и любых чисел
и любых чисел 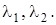
Область значений линейного оператора  является линейным многообразием
является линейным многообразием 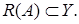
Оператор  называется непрерывным в точке
называется непрерывным в точке  если
если 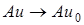 при
при 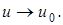
Теорема 1. Пусть 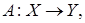
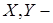 банаховы пространства
банаховы пространства 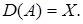 Если оператор
Если оператор  непрерывен в точке,
непрерывен в точке, 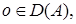 то он непрерывен в любой точке
то он непрерывен в любой точке 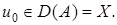
В самом деле, из 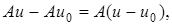 следует, что если
следует, что если 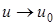 , то
, то 
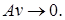 Ттогда
Ттогда 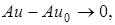 при
при 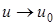 .
.
Отметим, что линейный оператор 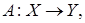
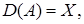
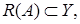 ограничен, если множество
ограничен, если множество 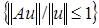 ограничено. Отсюда следует, что если
ограничено. Отсюда следует, что если  ограничен, то
ограничен, то 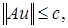
 для любого
для любого 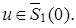
Теорема 2. Линейный оператор 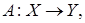 ограничен, тогда и только тогда, когда
ограничен, тогда и только тогда, когда 

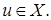
Доказательство. Пусть оператор  ограничен. Покажем, что
ограничен. Покажем, что 

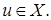 Пусть
Пусть 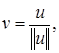
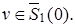 Тогда
Тогда 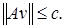 С другой стороны
С другой стороны 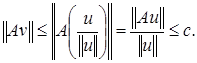 Отсюда имеем
Отсюда имеем 

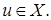
Пусть верно неравенство 

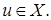 Покажем, что
Покажем, что  ограничен. В самом деле, в частности, при
ограничен. В самом деле, в частности, при 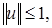 имеем
имеем 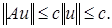 Это, означает, что для любых
Это, означает, что для любых 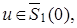
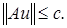 Теорема доказана.
Теорема доказана.
Теорема 3. Пусть 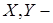 банаховы пространства,
банаховы пространства, 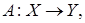
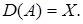 Оператор
Оператор  непрерывен, тогда и только тогда, когда он ограничен.
непрерывен, тогда и только тогда, когда он ограничен.
Доказательство. Необходимость. Пусть  непрерывен. Покажем, что
непрерывен. Покажем, что  ограничен. Предположим противное, т.е.
ограничен. Предположим противное, т.е.  неограничен. Тогда существует
неограничен. Тогда существует 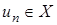 такой, что
такой, что 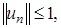
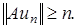 Пусть
Пусть  Так как
Так как 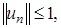 то
то 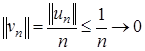 при
при 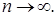 Так как оператор
Так как оператор  непрерывен, то
непрерывен, то 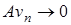 при
при 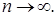 С другой стороны,
С другой стороны, 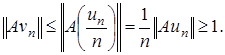 Из полученного противоречия следует, что оператор
Из полученного противоречия следует, что оператор  ограничен. Необходимость доказана.
ограничен. Необходимость доказана.
Достаточность. Пусть  ограничен. Покажем, что
ограничен. Покажем, что  непрерывен. Из ограниченности оператора, имеем
непрерывен. Из ограниченности оператора, имеем 

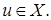 Оотсюда при
Оотсюда при  получим
получим  Это означает, что оператор
Это означает, что оператор  непрерывен в точке
непрерывен в точке  Тогда согласно теореме 1, оператор
Тогда согласно теореме 1, оператор  непрерывен в любой точке
непрерывен в любой точке  Достаточность доказана. Теорема доказана.
Достаточность доказана. Теорема доказана.
Пространства линейных операторов. Пусть  ,
,  ,
, 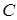 , … – линейные операторы, определенные в банаховом пространстве
, … – линейные операторы, определенные в банаховом пространстве 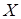 со значениями в банаховом пространстве
со значениями в банаховом пространстве 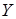 . На множестве линейных операторов введем операции сложения и умножения на число по правилу:
. На множестве линейных операторов введем операции сложения и умножения на число по правилу:
1) 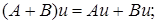
2) 
Можно показать, что для множества линейных операторов выполнены все аксиомы линейного пространства. Введем норму элемента, 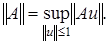 Заметим, что величина
Заметим, что величина 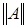 является наименьшей из констант в неравенстве
является наименьшей из констант в неравенстве 

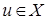 (см. теорему 2.). Очевидно, что
(см. теорему 2.). Очевидно, что
а)  если
если 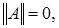 то
то  нулевой оператор;
нулевой оператор;
б) 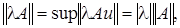
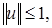
в) 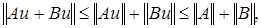
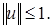
Отсюда имеем, 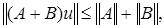

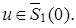 Выполнены все аксиомы нормы. Полученное нормированное пространство линейных непрерывных операторов действующих из
Выполнены все аксиомы нормы. Полученное нормированное пространство линейных непрерывных операторов действующих из 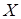 в
в 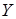 , обозначим через
, обозначим через 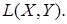
Пусть дана последовательность линейных операторов Говорят, что 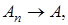
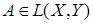 при
при  равномерно, если
равномерно, если 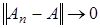 при
при  т.е. сходимость по норме пространства
т.е. сходимость по норме пространства 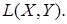
Теорема 4. Пусть 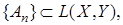
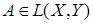 . Для того, чтобы
. Для того, чтобы 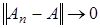 при
при  (равномерная сходимость), необходимо и достаточно, чтобы
(равномерная сходимость), необходимо и достаточно, чтобы 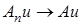 при
при  равномерно по
равномерно по 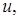
Доказательство. Необходимость. Пусть 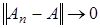 при
при  . Покажем, что
. Покажем, что 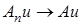 при
при  равномерно по
равномерно по 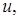
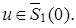 Ппоскольку
Ппоскольку  где
где 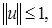
 при
при  , то
, то 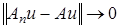 при
при  . Ииз
. Ииз 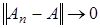 ,
,  следует, что
следует, что 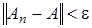 при
при  где
где 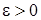 –любое число. Тогда
–любое число. Тогда 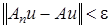 для любого
для любого 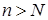 и для любого
и для любого 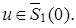 Это означает, что сходимость
Это означает, что сходимость  к
к 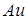 равномерно в
равномерно в 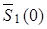 . Необходимость доказана.
. Необходимость доказана.
Достаточность. Пусть 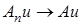 ,
,  равномерно по
равномерно по 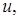
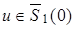 , т.е.
, т.е.  при
при 

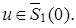 Покажем, что
Покажем, что 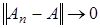 при
при  . Так как
. Так как 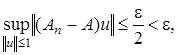 то согласно определению нормы линейного оператора, имеем
то согласно определению нормы линейного оператора, имеем 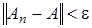 для любого
для любого 
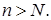 Отсюда имеем
Отсюда имеем 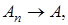
 . Достаточность доказана. Теорема доказана.
. Достаточность доказана. Теорема доказана.
Легко убедиться в том, что если 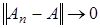 ,
,  , то
, то 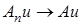 ,
,  равномерно по
равномерно по 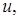
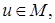 где
где 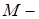 ограниченное множество в
ограниченное множество в 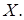
Теорема 5. Пусть 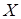 нормированное,
нормированное, 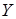 банахово пространство. Тогда пространство линейных операторов
банахово пространство. Тогда пространство линейных операторов 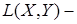 банахово.
банахово.
Доказательство. Пусть 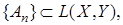 фундаментальная последовательность. Покажем, что любая фундаментальная последовательность
фундаментальная последовательность. Покажем, что любая фундаментальная последовательность 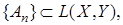 , т.е.
, т.е. 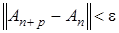 , для любых
, для любых  и любых натуральных
и любых натуральных  сходится к элементу
сходится к элементу 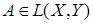 .
.
Рассмотрим последовательность 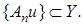 Ззаметим, что
Ззаметим, что
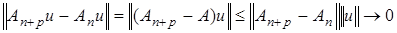
при  для любого натурального числа
для любого натурального числа  Это означает, что последовательность
Это означает, что последовательность  фундаментальна. Так как
фундаментальна. Так как 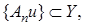
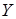 –банахово пространство то
–банахово пространство то 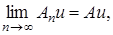
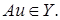 Остается показать, что
Остается показать, что 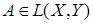 .
.
Легко убедиться в том, что  –линейный оператор. Покажем, что
–линейный оператор. Покажем, что  ограничен. Действительно, из фундаментальности числовой последовательности
ограничен. Действительно, из фундаментальности числовой последовательности 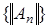 т.е.
т.е. 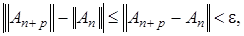 следует, что
следует, что 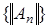 ограничена. Следовательно,
ограничена. Следовательно, 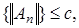
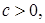
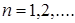 Тогда
Тогда  Отсюда переходя к пределу при
Отсюда переходя к пределу при  , получим
, получим 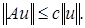 Это означает, что
Это означает, что  –линейный ограниченный оператор
–линейный ограниченный оператор 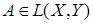 . Теорема доказана.
. Теорема доказана.
Определение 1. Говорят, что последовательность 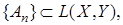 сильно сходится к элементу,
сильно сходится к элементу, 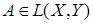 если
если 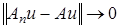 ,
,  для любого
для любого 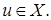
Заметим, что если 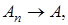
 равномерно, то
равномерно, то 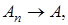
 сильно. В самом деле, из оценки
сильно. В самом деле, из оценки 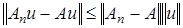 следует, что при
следует, что при 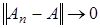
 ,
, 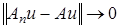 при
при  . Иными словами, из равномерной сходимости в
. Иными словами, из равномерной сходимости в 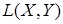 следует сильная сходимость в
следует сильная сходимость в 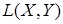 . Ооднако, обратное утверждение в общем случае, неверно.
. Ооднако, обратное утверждение в общем случае, неверно.
Лемма 1. Если 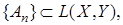 последовательность
последовательность 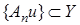 равномерно ограничена в замкнутом шаре,
равномерно ограничена в замкнутом шаре, 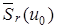 т.е.
т.е. 

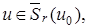 то числовая последовательность
то числовая последовательность  ограничена.
ограничена.
Доказательство. Пусть  Тогда
Тогда 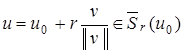 для любого
для любого  . Справедлива оценка
. Справедлива оценка
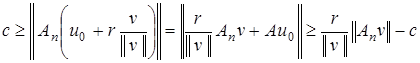 .
.
Отсюда имеем  ,
, 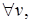
 Следовательно,
Следовательно, 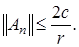 Лемма доказана.
Лемма доказана.
Теорема 6. (Принцип равномерной ограниченности) Пусть 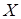 ,
, 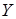 – банаховы пространства. Если
– банаховы пространства. Если 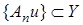 ограничена при каждом фиксированном
ограничена при каждом фиксированном 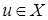 то
то 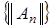 ограничена.
ограничена.
Доказательство. Пусть 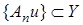 ограничена при каждом
ограничена при каждом 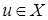 . Покажем, что
. Покажем, что 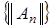 ограничена. Предположим противное т.е. числовая последовательность
ограничена. Предположим противное т.е. числовая последовательность 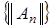 неограничена. Тогда последовательность
неограничена. Тогда последовательность  не ограничена ни в каком замкнутом шаре. Отметим, что если
не ограничена ни в каком замкнутом шаре. Отметим, что если 

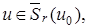 то согласно лемме было бы ограничена
то согласно лемме было бы ограничена 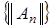 . Ииз неограниченности
. Ииз неограниченности  следует, что существуют замкнутые шары
следует, что существуют замкнутые шары 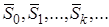 такие, что
такие, что 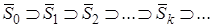 и на
и на 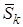 имеет место неравенство
имеет место неравенство  где
где 
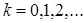 . Поскольку
. Поскольку 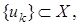
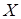 – банахово пространство, то по теореме вложенных шаров найдется точка
– банахово пространство, то по теореме вложенных шаров найдется точка 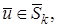
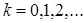 . такая, что
. такая, что 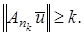 Это означает что последовательность
Это означает что последовательность 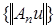 не ограничена. Это противоречит условию теоремы. Теорема доказана.
не ограничена. Это противоречит условию теоремы. Теорема доказана.
Теорема 7. (Теорема Банаха-Штейнгауза). Пусть 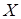 ,
, 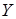 – банаховы пространства, последовательность
– банаховы пространства, последовательность 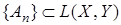 . Для того чтобы
. Для того чтобы 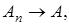
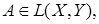
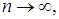 сильно, необходимо и достаточно чтобы
сильно, необходимо и достаточно чтобы
1) последовательность 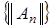 была ограничена;
была ограничена;
2) 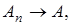
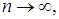 сильно, на линейном многообразии
сильно, на линейном многообразии 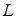 плотном в
плотном в 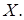
Доказательство. Необходимость. Пусть 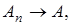
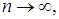 сильно. Покажем, что
сильно. Покажем, что 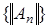 ограничена. Поскольку
ограничена. Поскольку 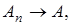
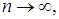 сильно, то согласно определению имеем
сильно, то согласно определению имеем 
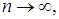

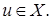 Отсюда следует, что
Отсюда следует, что 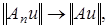
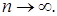 Следовательно
Следовательно  ограничена. Тогда по принципу равномерной ограниченности, последовательность
ограничена. Тогда по принципу равномерной ограниченности, последовательность 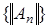 ограничена. В частности, последовательность
ограничена. В частности, последовательность 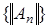 ограничена на
ограничена на 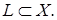 Необходимость доказана.
Необходимость доказана.
Достаточность. Пусть 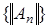 ограничена и
ограничена и 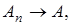
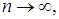 сильно на
сильно на 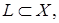
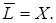 Покажем, что
Покажем, что 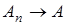 ,
, 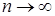 сильно на
сильно на 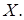 Пусть
Пусть 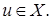 Так как
Так как 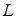 плотно в
плотно в 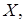 то найдется точка
то найдется точка 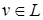 такая, что
такая, что 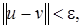
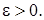 Поскольку
Поскольку 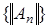 ограничена,
ограничена, 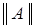 ограничена, то существует число
ограничена, то существует число 

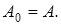 Тогда
Тогда
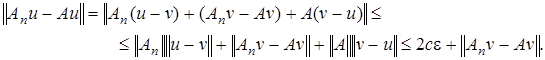
Так как 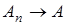 ,
, 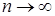 сильно на
сильно на 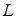 , т.е.
, т.е. 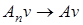 ,
, 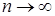 ,
, 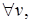
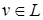 , то
, то 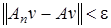 ,
, 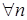 ,
, 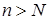 . Следовательно,
. Следовательно,  ,
, 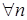 ,
, 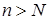 . Тогда
. Тогда 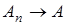 ,
, 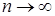 , сильно, в силу того, что
, сильно, в силу того, что 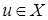 . Теорема доказана.
. Теорема доказана.
Пусть  ,
, 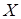 ,
, 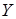 – банаховы пространства,
– банаховы пространства, 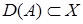 ,
, 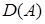 плотно в
плотно в 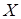 . Оператор
. Оператор  ограничен на
ограничен на 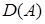 , если норма оператора
, если норма оператора 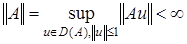 .
.
Теорема 8. (Теорема о продолжении линейного оператора по непрерывности). Пусть  ,
,  –банаховы пространства,
–банаховы пространства,  – линейный оператор, ограниченный на
– линейный оператор, ограниченный на 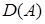 ,
, 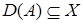 ,
, 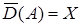 ,
, 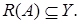 Тогда существует линейный ограниченный оператор
Тогда существует линейный ограниченный оператор 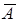 такой, что
такой, что
1) 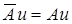 ,
, 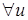 ,
, 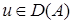 ;
;
2) 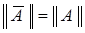 , где
, где  определен на всём
определен на всём 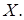
Доказательство. Пусть 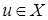 – произвольная точка. Так как
– произвольная точка. Так как 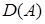 плотно в
плотно в 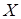 , то найдется последовательность
, то найдется последовательность 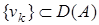 ,
, 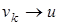 при
при 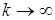 .
.
Определим оператор  на всем пространстве
на всем пространстве 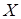 так:
так:  . Покажем, что
. Покажем, что 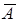 требуемое распространение оператора
требуемое распространение оператора 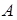 на всё
на всё 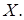 Действительно, если
Действительно, если 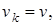 то
то 
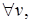
 Так как
Так как 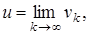 то
то 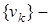 фундаментальна т.е.
фундаментальна т.е.  при
при 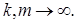 Заметим, что
Заметим, что  Отсюда следует, что последовательность
Отсюда следует, что последовательность 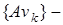 фундаментальная. Так как
фундаментальная. Так как 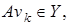
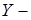 банахово пространство, то существует
банахово пространство, то существует 
Покажем, что 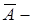 линейный оператор. Действительно, если
линейный оператор. Действительно, если 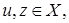
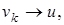
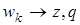
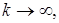 где
где 
 то
то  при
при 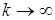 . Тогда
. Тогда
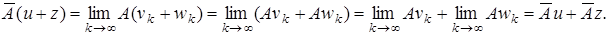 Покажем, что
Покажем, что 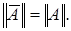 Пусть
Пусть 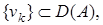


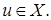 Тогда
Тогда 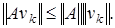 Переходя к пределу и учитывая непрерывность нормы, получим
Переходя к пределу и учитывая непрерывность нормы, получим  Отсюда следует, что
Отсюда следует, что 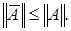 Однако
Однако
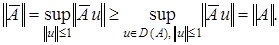
Из неравенств 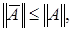
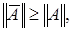 имеем
имеем 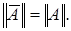 Теорема доказана.
Теорема доказана.
Обратные операторы. Пусть 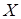 ,
, 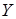 – банаховы пространства,
– банаховы пространства, 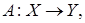
 –линейный оператор с областью определения
–линейный оператор с областью определения 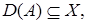 область значений
область значений 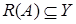 (иногда вместо
(иногда вместо 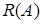 применяется обозначение
применяется обозначение  ).
).
Говорят, что оператор  обратимым, если для любого
обратимым, если для любого 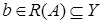 уравнение
уравнение 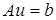 имеет единственное решение. Если
имеет единственное решение. Если  обратим, то каждому элементу
обратим, то каждому элементу 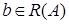 можно найти единственный элемент
можно найти единственный элемент 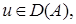 являющийся решением уравнения
являющийся решением уравнения  . Оператор осуществляющий это соответствие, называется обратным к
. Оператор осуществляющий это соответствие, называется обратным к  и обозначается
и обозначается  Множество
Множество  называется множеством нулей оператора
называется множеством нулей оператора  (иногда вместо
(иногда вместо 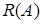 применяется обозначение
применяется обозначение 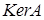 и называется ядром линейного оператора
и называется ядром линейного оператора  ).
).
Отметим, что:
1. Оператор 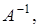 обратный линейному оператору
обратный линейному оператору  , также линеен. Действительно, если
, также линеен. Действительно, если 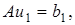
 то
то 
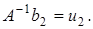 Тогда
Тогда 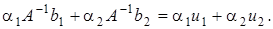 Так как оператор
Так как оператор  линеен, то
линеен, то 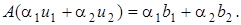 Следовательно,
Следовательно, 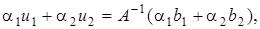 по определению обратного оператора. Отсюда следует, что
по определению обратного оператора. Отсюда следует, что 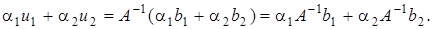 Это означает, что
Это означает, что 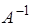 линеен.
линеен.
1. Оператор  переводит
переводит 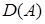 в
в 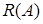 взаимно однозначно тогда и только тогда, когда
взаимно однозначно тогда и только тогда, когда 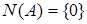 (либо
(либо 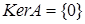 ).
).
Пусть 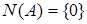 . Покажем, что оператор
. Покажем, что оператор  переводит
переводит 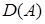 в
в 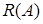 взаимно однозначно. Предположим противное т.е. образу
взаимно однозначно. Предположим противное т.е. образу 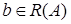 соответствует два прообраза
соответствует два прообраза 
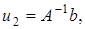 где
где 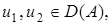


 Тогда
Тогда 
 Это означает, что
Это означает, что 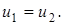
Пусть  взаимно однозначен. Покажем, что
взаимно однозначен. Покажем, что 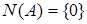 . Предположим противное т.е.
. Предположим противное т.е.  Пусть
Пусть 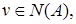
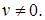 Пусть
Пусть 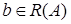 ,
, 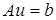 . Тогда
. Тогда 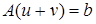 и
и 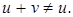 Отсюда следует, что образ
Отсюда следует, что образ 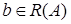 имеет два прообраза
имеет два прообраза 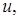
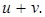 Это противоречит тому, что оператор
Это противоречит тому, что оператор  взаимно однозначен.
взаимно однозначен.
Определение 2. Говорят, что линейный оператор 
 непрерывно обратим, если:
непрерывно обратим, если:
а) оператор  обратим т.е. существует линейный оператор
обратим т.е. существует линейный оператор 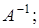
б) 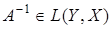 т.е. оператор
т.е. оператор 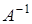 ограничен.
ограничен.
Теорема 9. Для того чтобы существовал ограниченный в 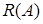 обратный оператор
обратный оператор 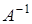 необходимо и достаточно, существования постоянный
необходимо и достаточно, существования постоянный 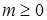 и для любого
и для любого 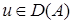 выполнения неравенства
выполнения неравенства
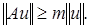 (1)
(1)
Доказательство. Необходимость. Пусть 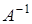 ограниченный в
ограниченный в 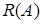 оператор. Покажем, что выполнено неравенство (1). Так как
оператор. Покажем, что выполнено неравенство (1). Так как 
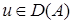 ,
, 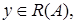 то из существования
то из существования 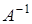 следует, что
следует, что 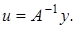 Поскольку
Поскольку 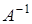 ограничен, то
ограничен, то 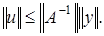 Отсюда имеем
Отсюда имеем 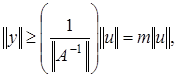 где
где 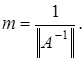 Следовательно,
Следовательно, 

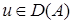 . Необходимость доказана.
. Необходимость доказана.
Достаточность. Пусть выполнено неравенство (1). Покажем, что существует ограниченный в 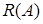 оператор
оператор 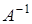 . Если
. Если 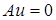 т.е.
т.е.  то из (1) имеем,
то из (1) имеем, 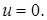 Отсюда следует, что
Отсюда следует, что 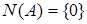 Тогда оператор
Тогда оператор  переводит
переводит 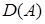 в
в 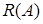 взаимно однозначно (см. выше п.2.). Это равносильно тому, что существует обратный оператор
взаимно однозначно (см. выше п.2.). Это равносильно тому, что существует обратный оператор 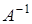 отображающий
отображающий 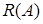 взаимно однозначно на
взаимно однозначно на 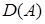 . Далее, из (1) при
. Далее, из (1) при 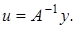 получим
получим 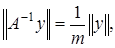
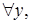
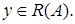 Это означает, что оператор
Это означает, что оператор 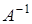 ограничен. Достаточность доказана. Теорема доказана.
ограничен. Достаточность доказана. Теорема доказана.
Из теоремы 9 при  имеем: Оператор
имеем: Оператор  непрерывно обратим тогда и только тогда, когда
непрерывно обратим тогда и только тогда, когда 
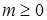 ,
, 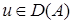 .
.
Лемма 2. Пусть  –всюду плотное множество в банаховом пространстве
–всюду плотное множество в банаховом пространстве  . Тогда любой ненулевой элемент
. Тогда любой ненулевой элемент  можно разложить в ряд
можно разложить в ряд

где  и
и 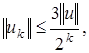
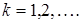
Доказательство. Пусть  . Последовательность
. Последовательность 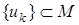 строим следующим образом: элемент
строим следующим образом: элемент 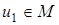 выберем так, чтобы
выберем так, чтобы 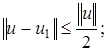 элемент
элемент 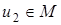 определим так, чтобы
определим так, чтобы 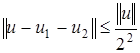 и т.д.
и т.д. 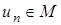 выберем так, чтобы
выберем так, чтобы 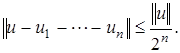 Такой выбор возможен, в силу того, что множество
Такой выбор возможен, в силу того, что множество  плотно в
плотно в  . Заметим, что
. Заметим, что 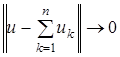 при
при 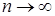 . Отсюда следует, что ряд
. Отсюда следует, что ряд  сходится к
сходится к  . Нормы элементов
. Нормы элементов 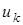 удовлетворяют неравенствам:
удовлетворяют неравенствам:

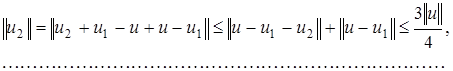

Лемма доказана.
Теорема 10. (Теорема Банаха об обратом операторе). Если  –ограниченный линейный оператор, отображающий взаимно однозначно банахово пространство
–ограниченный линейный оператор, отображающий взаимно однозначно банахово пространство 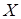 на банахово пространство
на банахово пространство 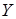 , то обратный оператор
, то обратный оператор 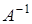 ограничен.
ограничен.
Доказательство. Так как оператор 
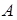 взаимно однозначно отображает банахово пространство
взаимно однозначно отображает банахово пространство 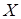 на банахово пространство
на банахово пространство 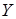 , то существует линейный обратный оператор
, то существует линейный обратный оператор 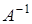 . Покажем, что
. Покажем, что 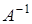 ограничен т.е.
ограничен т.е. 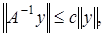
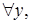
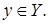
ведем в банаховом пространстве 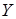 множества
множества 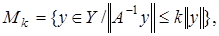 где
где 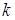 – любое натуральное число. Тогда
– любое натуральное число. Тогда 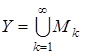 т.е. любой элемент
т.е. любой элемент  принадлежит некоторому
принадлежит некоторому 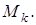 Согласно теореме Бэра банахово пространство
Согласно теореме Бэра банахово пространство 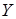 является множеством II категории т.е. любое множество
является множеством II категории т.е. любое множество 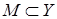 нельзя представить в виде объединение счетного числа нигде не плотных множеств. Отсюда следует, что хотя бы одно из множеств
нельзя представить в виде объединение счетного числа нигде не плотных множеств. Отсюда следует, что хотя бы одно из множеств  плотно в некотором шаре
плотно в некотором шаре 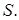 Пусть множество
Пусть множество  плотно в шаре
плотно в шаре 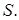 Рассмотрим шаровой слой
Рассмотрим шаровой слой

Перенося начало координат в точку 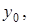 получим шаровый слой
получим шаровый слой 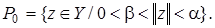 Покажем, что в
Покажем, что в 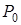 плотно некоторое множество
плотно некоторое множество  Пусть
Пусть 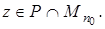 Тогда
Тогда  и норма
и норма 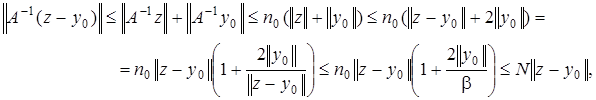
где 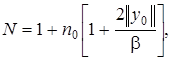
 –целая часть числа. Отсюда следует, что
–целая часть числа. Отсюда следует, что 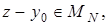 множество
множество 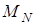 плотно в
плотно в 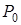 в силу того, что
в силу того, что  плотно в
плотно в 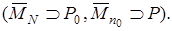

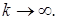
 .
.
Для любого элемента  можно найти число
можно найти число 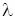 такое, что
такое, что  Тогда
Тогда 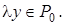 Так как
Так как 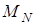 плотно в
плотно в 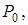 то найдется последовательность
то найдется последовательность 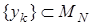 такая, что
такая, что 
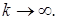 Отсюда следует, что последовательность
Отсюда следует, что последовательность  сходится к
сходится к 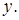 Заметим, что если
Заметим, что если  то и
то и  в силу того, что
в силу того, что 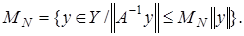 В самом деле, из
В самом деле, из 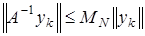 следует, что
следует, что 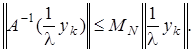 Поскольку
Поскольку  – произвольный элемент,
– произвольный элемент, 
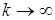 ,
,  ,
, 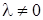 то множество
то множество 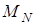 плотно в
плотно в 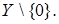 Следовательно,
Следовательно, 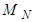 плотно в
плотно в 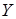 .
.
Пусть  ,
,  произвольный элемент. Согласно лемме 2 элемент
произвольный элемент. Согласно лемме 2 элемент 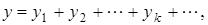
 где
где  Прообразы элементов
Прообразы элементов 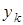 элементы
элементы  причем
причем 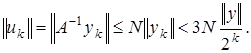 Рассмотрим ряд
Рассмотрим ряд 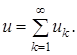 Норма
Норма 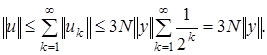 Следовательно, ряд
Следовательно, ряд 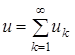 сходится. Так как
сходится. Так как  линейный ограниченный оператор т.е. непрерывный и ряд
линейный ограниченный оператор т.е. непрерывный и ряд 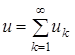 сходится, то
сходится, то 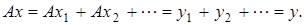 Отсюда, имеем
Отсюда, имеем 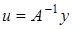 и
и 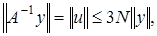
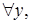
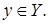 Это означает, что оператор
Это означает, что оператор 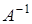 ограничен. Теорема доказана.
ограничен. Теорема доказана.
Определение 3. Прямой суммой 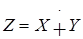 двух линейных пространств
двух линейных пространств 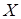 и
и 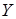 называется совокупность пар
называется совокупность пар 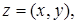

 для которых, если
для которых, если 
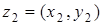 и
и 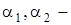 скаляры, то
скаляры, то 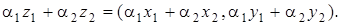 Норма в
Норма в  вводится так
вводится так 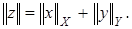
Определение 4. Графиком оператора 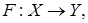

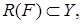
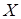 ,
, 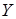 – банаховы пространства, называется совокупность пар
– банаховы пространства, называется совокупность пар 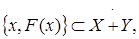 где
где 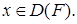
Определение 5. Линейный оператор  называется замкнутым, если его график является замкнутым множеством в
называется замкнутым, если его график является замкнутым множеством в  . Иными словами, замкнутость графика оператора
. Иными словами, замкнутость графика оператора 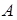 означает, что если
означает, что если 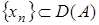 и
и 
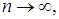 то
то 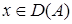 и
и 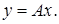
Отметим, что:
1) Пусть 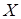 ,
, 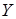 – банаховы пространства,
– банаховы пространства,  . Если
. Если  и
и
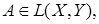 то
то  замкнут. В самом деле, если
замкнут. В самом деле, если 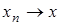 и
и  при
при 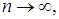 то
то 
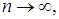 в силу непрерывности оператора
в силу непрерывности оператора  . Отсюда из единственности предела следует,
. Отсюда из единственности предела следует, 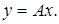 .
.
2) Если  замкнут и
замкнут и 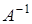 существует, то
существует, то 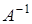 также замкнут. Поскольку множество
также замкнут. Поскольку множество 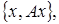
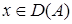 замкнуто, множество
замкнуто, множество