Конкретные банаховы и гильбертовы пространства

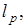
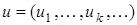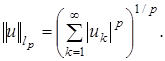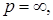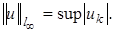1. Пространство Элементами являются с нормой В случае имеем с нормой Пространства , 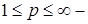банаховы,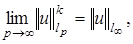

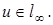
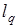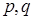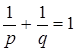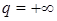Сопряженным к , является пространство , где связаны равенством , и при 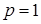. Пространство , рефлексивно.

Пространство 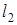гильбертово со скалярным произведением и с нормой .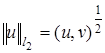

2.Пространства Лебега. Всякое нормированное пространство можно

рассматривать как линейное многообразие, плотное в некотором банаховом пространстве

Пусть нормированное пространство непрерывных функции 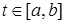с нормой

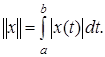
Банахово пространство является пополнением нормированного пространства . Пространство состоит из элементов являющихся классами эквивалентных в среднем последовательностей непрерывных функций. Помимо непрерывных функции 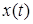класс содержит и разрывные функции, отличающих от функции 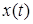в конечном числе точек. Разрывные функции можно интерпретировать как пределы в норме фундаментальных последовательностей непрерывных функции.

Пространство Лебега 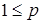является пополнением нормированного пространства 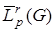непрерывных вектор функций с нормой

Элементами пространства Лебега 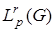являются некоторые «функции» приблизиться к некоторым с любой степенью точности (в среднем) можно с помощью непрерывных на функций. 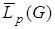плотно в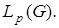

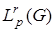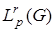Пространство. , Пространство , банахово, где 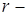целое положительное число, 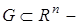измеримое по Лебегу множество. Элементами пространства 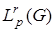(иногда встречаются обозначения 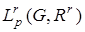) являются вектор функции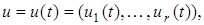 Норма в 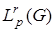определяется по формуле

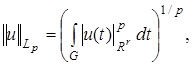
Если 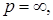то 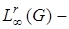банахово пространство ограниченных измеримых вектор функции с нормой

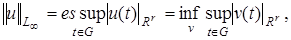
где 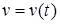пробегает множество всех измеримых вектор функции, совпадающих с 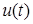почти всюду на Верно соотношение

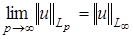для всех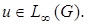

Если 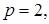то 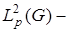гильбертово, со скалярным произведением

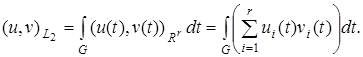
норма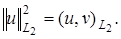

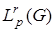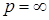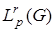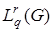Пространство , рефлексивно, а при оно является нерефлексивным. Сопряженным к , будет пространство , . Для 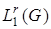сопряженным является пространство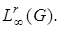

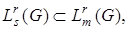Если то нормы

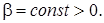
Из сходимости в 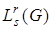по его норме следует сходимость по норме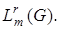

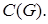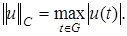3. Пространство Пространство состоит из непрерывных функции в замкнутом множестве с нормой Пространство 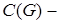банахово, нерефлексивно.

Теорема 2. (Теорема Рисса). Всякий линейный непрерывный функционал 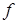на представим единственным образом в виде

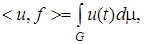
где 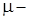регулярная борелевская мера на Норма

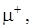
где 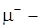положительная отрицательная составляющие меры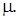

4.Пространства Соболева. Пусть 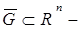заданная ограниченная замкнутая область.

Пусть 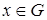непрерывно дифференцируемая раз функция, причем каждая частная производная функции 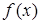имеет предел при стремлении 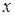к любой граничной точке области Граница 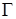области достаточно гладкая. Рассмотрим линейное пространство таких функции 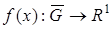с нормой

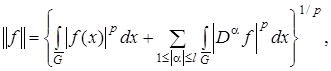
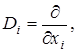
где 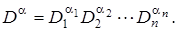Полученное нормированное пространство обозначим через 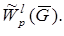Пополнением нормированного пространства является банахово пространство 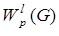и оно называется пространством Соболева.

В случае 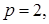имеем Пространство Соболева 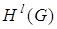является гильбертовым пространством. В частности, пространство 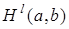является пополнением пространства 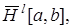состоящее из всевозможных функций непрерывно дифференцируемых на со скалярным произведением

и нормой

Элементами являются классы, состоящие из последовательностей 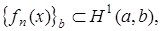фундаментальных в таких, что

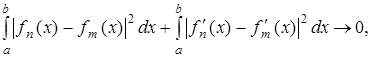
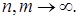
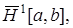Из условия фундаментальности в среднем в имеем

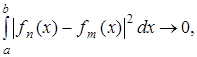
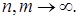
Тогда согласно определению пространства 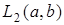существуют функции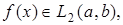 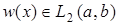такие, что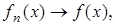 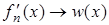в

среднем при 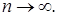Функция 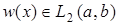называется обобщенной производной (в смысле Соболева) функции 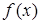и пишется

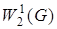4.1.Пространство (или ). Элементами пространства являются функций обладающих обобщенными производными 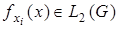по всем переменным 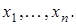Скалярное произведение определяется выражением

3) норма элемента Пространство –гильбертово, рефлексивно.

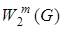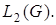4.2.Пространство (или ). Элементами пространства являются функций обладающих всеми обобщенными частными производными до порядка включительно из Скалярное произведение

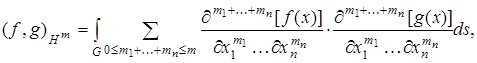
Норма 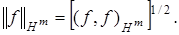Пространство –гильбертово, рефлексивно.

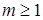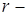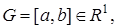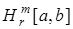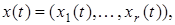
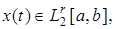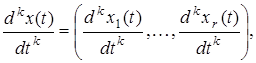
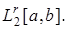4.3.Пространство (или ). Элементами являются мерные вектор функций и является обобщением пространства . В частности, когда элементами пространства являются функции обладающих обобщенными производными из Скалярное произведение

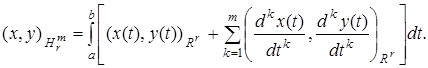
Норма 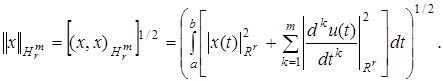Пространство – гильбертово, рефлексивно.

4.4.Пространство Множество 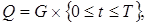где 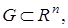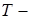заданное положительное число. Элементами пространства являются функции 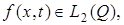обладающих обобщенными частными производными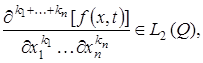 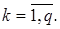Скалярное произведение

Норма 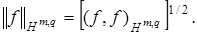Пространство 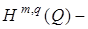гильбертово, рефлексивно.

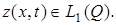Пусть Пусть функция Функция называется следом функции при 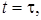если для любого найдется число такое, что для почти всех 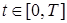для которых 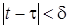имеет место неравенство

Если след функции при существует, то его обозначает через 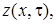или Аналогично определяется след 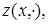при каждом фиксированном .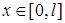

Дата добавления: 2014-01-07