
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 8. Функциональные пространства
|
|
|
|
Приведены сведения о гильбертовых, сопряженных, рефлексивных пространствах. Рассмотрены конкретные банаховы и гильбертовы пространства встречающихся в теории экстремальных задач.
Гильбертовы пространства. Пространство со скалярным произведением называется гильбертовым, если оно полно в норме, порожденный скалярным произведением. Гильбертовы пространства обозначают буквой 
Теорема 1. (Теорема Ф. Рисс). Пусть  гильбертово пространство. Для любого линейного ограниченного функционала
гильбертово пространство. Для любого линейного ограниченного функционала 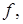 заданного всюду на
заданного всюду на 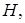 существует единственный элемент
существует единственный элемент  такой, что
такой, что 
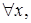
 причем
причем 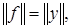 где
где 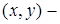 скалярное произведение элементов
скалярное произведение элементов 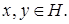
Доказательство. Пусть множество 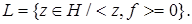 Если
Если  то
то 
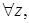
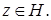 Тогда
Тогда  В этом случае, можно принять
В этом случае, можно принять  Итак,
Итак, 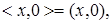
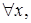

Пусть 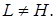 Тогда существует элемент
Тогда существует элемент 
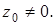 Не умаляя общности, можно считать, что
Не умаляя общности, можно считать, что 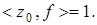 Действительно, в противном случае вместо
Действительно, в противном случае вместо  можно взять
можно взять  Тогда
Тогда 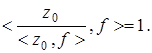 Легко убедиться в том, что элемент
Легко убедиться в том, что элемент 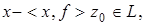
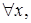
 В самом деле,
В самом деле,
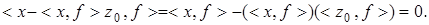
Так как 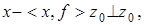 то скалярное произведение
то скалярное произведение

Отсюда имеем
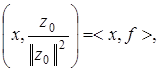
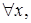

Если принять 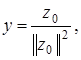 то
то 
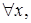
 Таким образом, установлена взаимно однозначное соответствие между элементами пространств и
Таким образом, установлена взаимно однозначное соответствие между элементами пространств и 
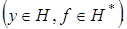
Покажем, что 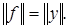 Поскольку
Поскольку  в силу неравенства Коши-Буняковского, то
в силу неравенства Коши-Буняковского, то  по определению нормы функционала. Так как
по определению нормы функционала. Так как  то
то  Тогда
Тогда 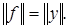
Докажем единственность 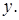 Предположим, что кроме
Предположим, что кроме  существует другой элемент
существует другой элемент 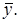 Тогда
Тогда 
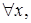
 Отсюда имеем
Отсюда имеем 
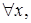
 Тогда
Тогда  Следовательно,
Следовательно,  Теорема доказана.
Теорема доказана.
Из данной теоремы следует, что пространство, сопряженное к гильбертову пространству  «совпадает» с
«совпадает» с  Тогда
Тогда 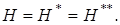 Если
Если  то
то 
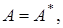 где
где  самосопряженный оператор.
самосопряженный оператор.
Сопряженные пространства. Пусть 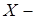 банахово пространство,
банахово пространство, 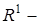 числовая ось. Пространство линейных ограниченных функционалов, заданных на
числовая ось. Пространство линейных ограниченных функционалов, заданных на 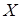 называется сопряженным к
называется сопряженным к 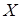 и обозначается
и обозначается 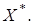
Таким образом, 
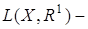 банахово пространство (см. теорему 5, лекция 6, где
банахово пространство (см. теорему 5, лекция 6, где  банахово). Значение линейного ограниченного функционала
банахово). Значение линейного ограниченного функционала  на элементе
на элементе  равно
равно 
Отметим, что:
1) Если 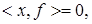
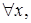
 то
то 
2) Если 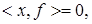

 то
то 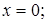
3) 
4) Сходимость по норме 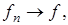
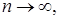 если
если 
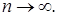
5) Слабая сходимость 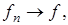
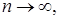
 слабо, если
слабо, если 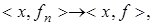
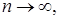
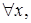
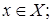
6) Принцип равномерной ограниченности: если  ограничена при каждом
ограничена при каждом  то
то 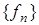 ограничена (см. теорему 6, лекция 6);
ограничена (см. теорему 6, лекция 6);
7) Теорема Банаха-Штейнгауза: для того чтобы 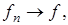
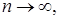
 слабо, необходимо и достаточно, чтобы:
слабо, необходимо и достаточно, чтобы:
а)  была ограничена;
была ограничена;
б) 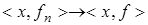 на плотном в
на плотном в 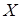 линейном многообразии.
линейном многообразии.
Рефлексивные пространства. Пусть 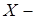 банахово пространство,
банахово пространство,  сопряженное пространство (банахово). Сопряженное к
сопряженное пространство (банахово). Сопряженное к  пространство
пространство  банахово. Пространство
банахово. Пространство  банахово и т.д.
банахово и т.д.
Теорема. Если 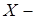 банахово пространство, то
банахово пространство, то 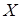 изометрично вложено в
изометрично вложено в 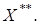
Доказательство. Отметим, что 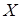 изометрично вложено в
изометрично вложено в 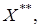 если
если  где
где 
 Пусть
Пусть 
 Значение функционала
Значение функционала 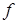 на элементе
на элементе 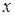 равно
равно  Теперь рассмотрим случай, когда
Теперь рассмотрим случай, когда 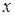 фиксирован, а
фиксирован, а 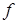 меняется. Тогда каждому
меняется. Тогда каждому  ставится в соответствие определенное число
ставится в соответствие определенное число 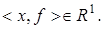 Заметим, что элементу
Заметим, что элементу  ставится в соответствие число
ставится в соответствие число

Справедливо неравенство  Отсюда следует, что
Отсюда следует, что 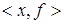 определяет заданный всюду в
определяет заданный всюду в  линейный ограниченный функционал
линейный ограниченный функционал  такой, что
такой, что
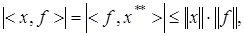


где  С другой стороны, из следствия 1 теоремы Хана-Банаха (см. лекция 4) следует, что существует функционал
С другой стороны, из следствия 1 теоремы Хана-Банаха (см. лекция 4) следует, что существует функционал 
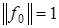 такой, что
такой, что 
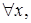
 Тогда
Тогда  Следовательно,
Следовательно, 
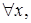


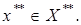 Теорема доказана.
Теорема доказана.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 601; Нарушение авторских прав?; Мы поможем в написании вашей работы!