Доказательство.Заметим, что , , ,

Если 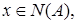то верно равенство 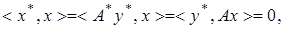в силу того, что 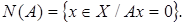Тогда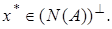

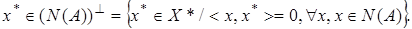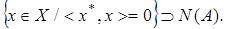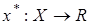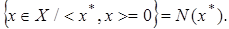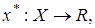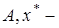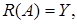
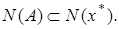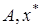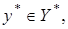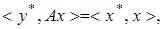
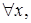
Пусть Тогда множество Если линейный оператор, то множество Рассмотрим операторы: ; где линейные непрерывные операторы, Для операторов выполнены все условия следствия 2. Тогда существует такой линейный непрерывный функционал что Отсюда следует, что 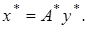Следовательно, 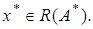Лемма доказана.

Лемма 4. Пусть 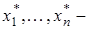линейные непрерывные функционалы на банаховом пространств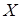е т.е. 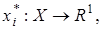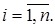Пусть 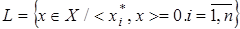подпространство в 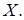Тогда аннулятор 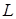совпадает с линейной оболочкой точек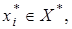

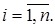
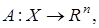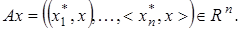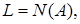
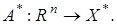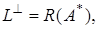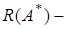Доказательство. Рассмотрим оператор где Тогда Cогласно лемме 3, имеем где линейная оболочка точек 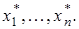Лемма доказана.

Нормально-разрешимые операторы. Пусть 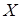, 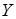– банаховы пространства,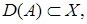

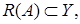
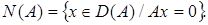
Теорема 12. Пусть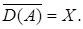Тогда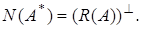

Доказательство. Как следует из условия теоремы множество 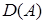плотно в 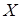следовательно существует сопряженный оператор 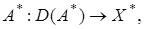где 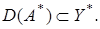Необходимо доказать, что ортогональное дополнение к области значения оператора 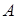совпадает с множеством нулей сопряженного оператора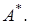

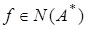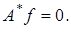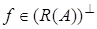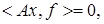
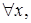
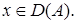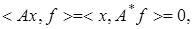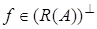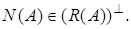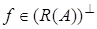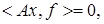
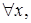
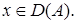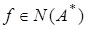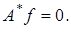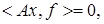
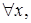
Пусть т.е. Покажем, что т.е. Так как то . Отсюда следует, что Пусть, обратно, т.е. Покажем, что т.е. Из 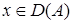следует,

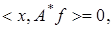
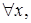
что 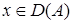. Так как 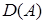плотно в 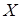то равенство 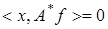возможно, только при 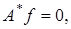где 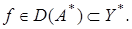Следовательно, 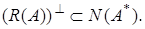Теорема доказана.

Теорема 13. Пусть 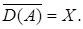Тогда 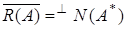(т.е. замыкание множества значений оператора 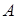состоит из тех и только тех элементов 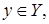которые ортогональны к каждому решению однородного сопряженного уравнения)

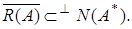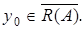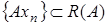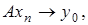
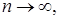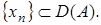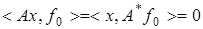Доказательство. Покажем, что Берем любой элемент Тогда существует последовательность такая, что где Пусть любой элемент. Тогда для любого 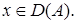Отсюда следует, что 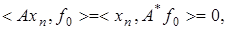в силу того, что 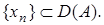Заметим, что элементами 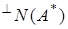являются: 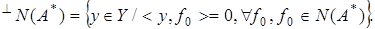Покажем, что 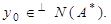Действительно, 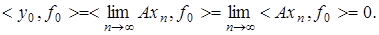Тогда 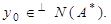Итак, доказано включение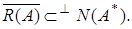

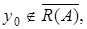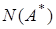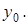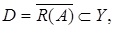
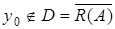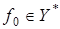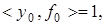
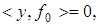
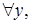
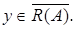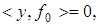
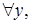
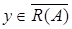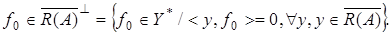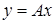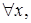
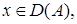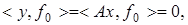
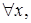
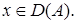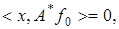
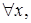
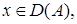
Теперь для доказательства теоремы достаточно показать, что если то множество содержит элемент не ортогональный к Согласно следствию 2 теоремы Хана-Банаха (см.. лекцию 4, где ) существует функционал такой, что Соотношение равносильно тому, что Так как , то Отсюда имеем 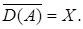Следовательно, 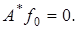С другой стороны из равенства 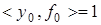следует 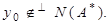Таким образом, если 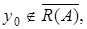то существует элемент 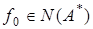не ортогональный к 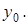Теорема доказана.

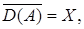
Определение 6. Оператор 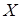, 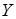– банаховы пространства называется нормально-разрешимым, если 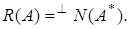Иными словами, оператор 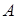нормально-разрешимый, если 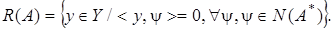Рассмотрим уравнение 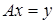и сопряженное однородное уравнение 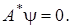Если оператор 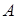нормально разрешимы, то верны следующие утверждения: а) если уравнение 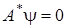имеет только нулевое решение, то уравнение 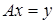имеет решение для любого 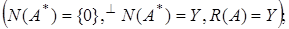б) если уравнение 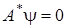имеет не нулевое решение, то уравнение 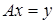имеет хоть одно решение в том и только в том случае, когда 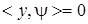для любого решения 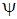уравнения .

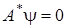Теорема 14. (Теорема Хаусдорфа). Пусть 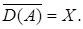Оператор 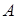нормально-разрешимый тогда и только тогда, когда 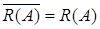т.е. оператор 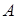имел замкнутую область значений.

Доказательство. В случае 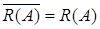из теоремы 13 следует, что 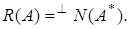Это означает, что оператор 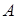нормально разрешимы (см. определение).

Пусть 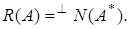Покажем, что 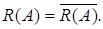Как следует из теоремы 13, 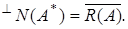Тогда 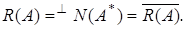Теорема доказана.

Дата добавления: 2014-01-07