Комплексные числа

4.1. Определение комплексных чисел

В связи с задачей решения квадратных уравнений при отрицательных значениях дискриминанта возникла необходимость расширения множества действительных чисел, необходимость введения чисел более общей природы, аналогично тому, как и ранее вводились расширения . Действительные числа уже будут частным случаем этих «новых» чисел.

Комплексным числом называется выражение z =x+iy, где x и y – действительные числа, а i – символ, который называется мнимой единицей: i²= -1. Символ i ввел Л.Эйлер в 1777 году, а понятие комплексного числа Р.Декарт в 1637 г.

Например, корни у равнения x ²+4 x +13=0,

D ₁= 4 -13=-9 теперь можно записать в следующем виде

z ₁ = (2+3 i), z ₂ = (2-3 i).

Числа х и y называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются символами:

x = Re z, y = Im z

Два комплексных числа 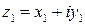и равны тогда и только тогда, когда равны их действительные и мнимые части, т.е. 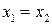и . Число называется нулем. Число называется единицей.

Если y = 0, то число z = x + i 0 считается совпадающим с действительным числом x. Если x = 0, то z = 0 + i y обозначается просто i y и называется чисто мнимым числом.

Геометрическая интерпретация комплексного числа.

Выберем на плоскости декартову прямоугольную систему координат и будем рассматривать упорядоченную пару чисел (x,y) как координаты точек этой плоскости.

Тогда каждому числу z = x + iy будет отвечать определённая точка z (x,y) плоскости и, наоборот, каждой точке плоскости будет отвечать определённое число z = x + iy.

Таким образом, между множеством комплексных чисел и множеством точек плоскости Оху существует взаимно однозначное соответствие, значит, каждое комплексное число можно интерпретировать как пару действительных чисел, т.е. как элемент пространства .

Плоскость Оху называется комплексной плоскостью. Действительные числа изображаются при этом точками оси Oх. Ось Oх называется действительной осью. Чисто мнимые числа z = iy изображаются точками на оси Oу, которая называется мнимой осью.

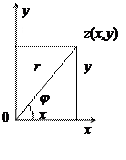Комплексное число z = x + iy можно интерпретировать и как вектор с координатами (x,y).

Рис.1

Впервые комплесные числа стал геометрически изображать датский землемер Вессель.

4.2. Различные формы записи комплексного числа

1. Алгебраическая форма:

z = x + iy. (1)

Два комплексных числа z ₁ = x ₁ + iy ₁ и z ₂ = x ₂ + iy ₂ равны друг другу (z ₁ = z ₂) тогда и только тогда, когда

x ₁ = x ₂, и y ₁ = y ₂

Если x ₂ = x ₁, а y ₂ = - y ₁, то комплексные числа z₁ = z₂ называются взаимно сопряжёнными:

z = x + iy, = x – i y.

Точки z (x,y) и z (x,-y) симметричны относительно действительной оси Oх.

2. Тригонометрическая форма.

Введём в рассмотрение радиус-вектор точки z и угол φ, образованный им с положительным направлением оси Oх. (рис.1).

Величины r и φ называются, соответственно, модулем и аргументом комплексного числа z и обозначаются символами:

r = | z |; φ = Arg z.

Модуль комплексного числа определяется однозначно формулой (из треугольника, рис 1);

r = | r |

Все значения аргумента φ удовлетворяют соотношению

,

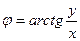
Угол φ называется аргументом комплексного числа z:

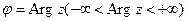
Аргумент определяется не однозначно, а с точностью до числа, кратного 2 π. Если z =0, то аргумент произволен.

Наименьшее по модулю значение аргумента Arg z называется его главным значением:

или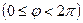

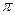, x > 0, y > 0;

- , x < 0, y > 0;

Arctg z =

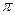+ , x < 0, y < 0;

2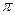- , x > 0, y < 0;

Главное значение аргумента определяется однозначно. Очевидно:

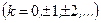
Из треугольника: x = cos φ и y = sin φ. Поэтому любое комплексное число можно записать в тригонометрической форме:

или (= r)

(2)

Два комплексных числа z ₁ и z ₂ равны тогда и только тогда, когда равны их модули, а аргументы равны или отличаются на 2 кπ:

;

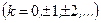
Для перехода от алгебраической формы (1) к тригонометрической (2) пользуются равенствами:

; .

Пример 1. Записать комплексные числа в тригонометри-

ческом виде

Рис.2.

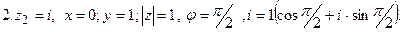
Пример2. Записать комплексное число 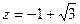ί в тригонометрическом виде.

Решение: .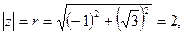

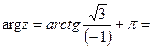
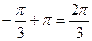Поэтому 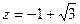ί=.

3. Показательная форма.

Рассмотрим показательную функцию с мнимым показателем . Использование формулы Эйлера

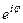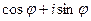= (3)

позволяет перейти от тригонометрической формы записи комплексного числа к показательной или экспоненциальной форме:

Вывод этой формулы содержится в теории рядов. С её помощью от тригонометрической формы (2) записи комплексного числа можно перейти к показательной:

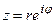(4)

Учитывая, что i² = -1;

e^x = 1 + x + +... + + …;

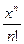e^z = 1 + z + 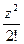+... + + …, где z – комплексное число;

e^iz = 1 + iz - - + …;

e^-iz = 1 - iz - + + + …;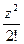

Примеры: Записать комплексные числа в показательной форме.

Правая часть формулы (3) есть комплексное число с модулем, равным 1:

i

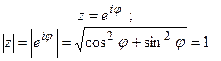(5)

х

Значит, равенство (5) на плоскости (z) определяет окружность единичного радиуса с центром в начале координат.

.

Рис. 3.

При φ =0 z ==1; при φ=π /2 z= =I и т.д. Таким образом, при изменении φ от 0 до 2 π точки z =опишет окружность единичного радиуса против часовой стрелки.

В отличии от функции , функция в силу формулы Эйлера периодическая с периодом T = 2 π.

4.3. Действия над комплексными числами

На множестве комплексных чисел определены те же действия, что и на множестве действительных чисел. Пусть

и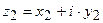

а) Сумма и разность двух комплексных чисел определяется следующим образом:

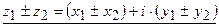
т.е. при сложении комплексных чисел их действительные и мнимые части складываются, а при вычитании вычитаются.

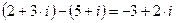
Модуль суммы комплексных чисел меньше либо равен сумме модулей этих чисел:

Доказательство: принимая во внимание, что модуль комплексного числа равен длине соответствующего этому числу вектора и что одна сторона треугольника короче суммы двух других сторон, то . Причем знак будет иметь место лишь в том случае, когда векторы соответствующих комплексных чисел z₁ и z₂ одинаково направлены, т. е. когда аргументы этих чисел равны или отличаются на кратное 2.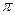

1) фиолетовой линией обозначено z₂;

2) синей линией обозначено z₁;

3) красной линией обозначена разность z₁ - z₂;

4) черной линией обозначена сумма z₁ + z₂;

Дата добавления: 2014-01-07