Моделирование транспортных потоков

Установление закономерностей между различными ха­рактеристиками транспортного потока может быть осуществле-о методами математического моделирования При моделиро­вании транспортных потоков различают два основных подхода ^ акро- и микроскопический

Макроскопический подход характеризуется созданием макро-\оделей описывающих состояние потока в виде взаимосвязи основных его характеристик Типичным примером макромодели рзляется уравнение, описывающее связь интенсивности, плот­ности и скорости N(x, ti, t-t} = q(ti, Xi, Xi)v(x\; xi, t) Для опи-"•"ния тпанспортного потока часто пользуются аналогиями Например в основе гидродинамической модели заложено пред-

-авлечге о движении одномерного потока сжимаемой жидко-l~h. В этой модели рассматривается наличие двух условии Первое условие допускает, что если интенсивность с расстоя-" 1ем уменьшается, то плотность с течением времени должна гасти, т е общее число автомобилей на рассматриваемом \частке остается постоянным во времени dn/dt = 0 Это значит,

то число входящих автомобилей на участок равно числ^ выхо­дящих Этот принцип математически записывается в виде урав-

ения неразрывности [1]

ЭЛ7Э5 + Э^/Э< = О

Второе условие допускает, что если плотность с расстоянием зеличивается, то скорость с течением времени уменьшается. Это объясняется естественным снижением скорости водителем

-\эи движении в более плотном транспортном потоке Этот прин-

- in описывается уравнением движения

Э./Qt=-(C'^!!q)(Эq|ЭS)

-е С — постоянная

Используя гидродинамическую модель, Д Дрю предложил ледующее соотношение между скоростью и плотностью [10]

^ =. (1 —^/^max)¹"-¹'/² ДЛЯ П> —1

-е т- — скорость двнжечия в свободных условиях q, — тотчо^ть потол^ е / й точке диаграммы, qmas — максимальная тотчо^ть потока

12С

При п = 1 уравнение преобразуется ^ линейную модель-Гриншилдса

v = v,(\ —qJqvm). ~^

'При п. = — 1 уравнение преобразуется в экспоненциальную

модель Гринберга _

V = (OnJn^max)/'?.,), Г

-где i „ — скорость, соответств; ющая максимальной интенсивности ~~_

Движение транспортного потока может быть описано, кроме, того. микромоделями, в которых используются закон сохране-" ния количества движения, закон сохранения энергии, метод^ кинем ^tt's el'⁷?' ^^^^ ^{тт гг} ^

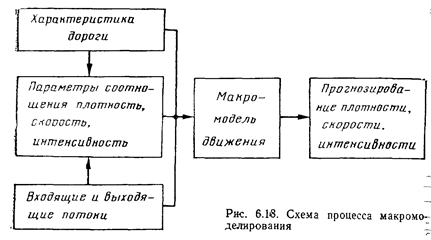
Макролюделирование (рис. 6.18) позволяет, оперируя значе-_ нием о начальном состоянии потока и характеристиках дороги,-прогнозировать изменение плотности, скорости и интенсивности.

Микроскопический подход преследует цель более деталь-" ного представления взаимодействия автомобилей в транспорч-ном потоке. Это взаимодействие описывается так называемой моделью следования за лидером. В основу этой модели поло­жена подтвержденная экспериментально гипотеза о взаимосвя­зи между скоростью и ускорением движения ведомого и лиди­рующего автомобиля [34]:

dv,-t(t + t)/w = /.[»,(/) --J,-i (О],

где a:' _i(r—T)W: — ускоре-ii'e ведомого ав^мобиля с \четом реакции во­дителя (задержки) г, заменяющейся в пределах 1,0.. 2,2 с; ). — показа­теля, характеризующий реакцию водителя на изменение режима движения лидера, называемый показателем чувствительности и равный 1//р; v, — ско­рость i-ro автомобиля.

Дальнейшее развитие этого принципа приводит к созданию более сложных нелинейных моделей Микромодели хорошо опи­сывают процесс на небольших участках дорог (I... 1,5 км) за сравнительно короткие периоды (до 30 мин).

Одной из важнейших характеристик транспортного потока является интервал движения автомобилей друг за другом. Рас­пределение интервалов является случайным событием, поэтому может быть описано существующими вероятностными законами как дискретными (распределение Пуассона, биномиальное, ги-лергеометрическое и др.), так и непрерывными (распределения Пирсона, нормальное, Вейбулла, Эрланга, Максвелла, экспо­ненциальное н др.).

Наиболее широкое применение в теории транспортных пото­ков нашли распределения Пуассона, Пирсона, Эрланга. Кроме того, в последнее время для математического описания транс­портного потока находят применение марковские случайные процессы, рассматривающие вероятность состояния системы в будущем {t > to) в зависимости от ее состояния в настоящем [t = to) при условии независимости от того, когда и каким об­разом система пришла в это состояние. В частности, при опре­делении разрыва в потоке может быть использовано эрланговое распределение интервалов в пересекаемом транспортном пото­ке. При рассмотрении маневров обгона, смены полосы движе­ния могут быть использованы марковские процессы и т. д. Например, транспортный поток небольшой плотности хорошо описывается распределением Пуассона [10]:

Р,(п) =[(^)"е-"]/га!,

где Pt{n) — вероятность появления в данном сечении дороги п автомобилей за интервал t; q — среднее число автомобилеи за единицу времени; qt — среднее число автомобилей за интервал г

Потоки средней и большой плотности более достоверно опи­сываются распределениями: нормальным, логарифмически нор­мальным, гамма-распределением и др.

Дата добавления: 2014-01-07