Вероятности непрерывной случайной величины

Функция распределения и функция плотности

Определение непрерывной случайной величины.

ПОНЯТИЕ О НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИНАХ

Дискретная случайная величина – это числовая функция, область определения которой есть конечное или счетное множество элементарных исходов. Множество ее значений также конечно или счетно. Но счетное множество элементарных исходов – лишь небольшой частный случай пространства W.

Рассмотрим случайную величину , значения которой целиком заполняют некоторый интервал или всю числовую ось. Одновременно задается функция распределения случайной величины Х:

. (10.1)

Случайную величину Х будем называть непрерывной, если функция F (x) дифференцируема (следовательно, F (x) непрерывна) и ее производная

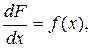
(10.2)

является кусочно-непрерывной функцией. Функция f (x) называется функцией плотности вероятности случайной величины X. Перечислим некоторые свойства функций F (x) и f (x).

1. 0 £ F (x) £ 1.

2. Если x ₂ > x ₁, то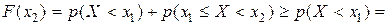

неубывающая функция.

3.

4. .

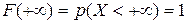5.

= D xf (x ₀)=0, для любого .

Таким образом, вероятность любого элементарного исхода ω равна нулю.

6. так как

+

, (х ₂ > х ₁).

Итак, если Х – непрерывная случайная величина, то равна нулю вероятность любого события вида {“случайная величина Х приняла значение х ₀”}, отличными от нуля могут быть только вероятности событий вида {“случайная величина Х приняла значение из интервала (a, b), ”}.

7. По формуле Ньютона - Лейбница

.

Соглашение о кусочной непрерывности функции f (x) гарантирует существование интеграла.

8. Производная неубывающей функции неотрицательна, f (x) ³ 0.

Если для некоторого числа x ₀ значение f (x ₀) = 0, то говорят, что случайная величина X не принимает значения x ₀; если же f (x ₀) > 0, то говорят, что случайная величина X может принять значение x ₀.

9. , ведь событие 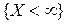является достоверным событием.

10. (10.3)

Этот интеграл – есть функция своего верхнего предела х, поэтому подынтегральная переменная обозначена другой буквой.

Будем говорить, что непрерывная случайная величина Х задана (или задан закон распределения непрерывной случайной величины Х), если определена одна из двух функций – функция распределения F (x) или функция плотности вероятности f (x). Зная одну из этих функций, можно определить другую (см. формулы (10.2), (10.3)).

Дата добавления: 2014-01-07