
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Первый замечательный предел
|
|
|
|
Замечательные пределы
Сложная функция и ее непрерывность
Пусть функция x=j(t) задана на множестве {t}, и пусть {x}- множество ее значений. Допустим, что на множестве {x} задана функция y=f(x). Тогда на множестве {t} задана сложная функция y=f(j(t))=F(t). Предположим, что aÎj(t) является предельной точкой множества {t}; aÎj(t); b=j(a) Î {x} является предельной точкой множества {x}.
Теорема. Пусть
x=j(t) Î C{a}, y=f(x) Î C{b}, где b=j(a). Тогда y=f(j(t))=F(t) Î C{a}.
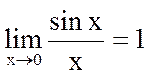
Доказательство. Сначала установим справедливость неравенства 0<sinx<x<tgx при 0<x<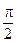 . (1)
. (1)
Рассмотрим следующие фигуры (см. рис. 1):
треугольники AOB и АОС и сектор АОВ
Для них
SDAOB<Sсект. АОВ<SDАОС, т.е.
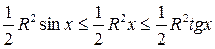 .
Сокращая на .
Сокращая на 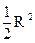 , получаем неравенства (1)
Пусть 0<x< , получаем неравенства (1)
Пусть 0<x<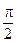 . .
|
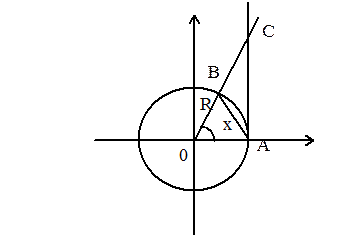 рис.10
рис.10
|
Из (1) деля на sinx, имеем 0<1<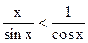 или
или
cosx<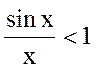 .
.
Эти неравенства справедливы и для значений x, удовлетворяющих условиям 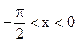 , так как cosx=cos(-x) и
, так как cosx=cos(-x) и 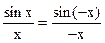 . Функция y=cosx - непрерывна на всей числовой оси (см., например, Ильин В.А., Позняк Э.Г. Основы математического анализа.- М.: Наука, 1971, ч.1, гл.4, *5, п.6, с.120) поэтому
. Функция y=cosx - непрерывна на всей числовой оси (см., например, Ильин В.А., Позняк Э.Г. Основы математического анализа.- М.: Наука, 1971, ч.1, гл.4, *5, п.6, с.120) поэтому 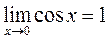 . Итак, для функции cosx, 1,
. Итак, для функции cosx, 1,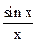 в некоторой d-окрестности точки x=0 выполняются все условия теоремы 2 п.3.12. о предельном переходе в функциональных неравенствах(f(x)=cosx, g(x)=1, h(x)=
в некоторой d-окрестности точки x=0 выполняются все условия теоремы 2 п.3.12. о предельном переходе в функциональных неравенствах(f(x)=cosx, g(x)=1, h(x)= 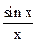 и d=
и d=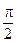 ).
).
Следовательно, 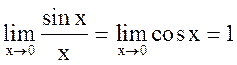 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 376; Нарушение авторских прав?; Мы поможем в написании вашей работы!