Абсолютная и условная сходимость

Перейдём теперь к рядам с членами, имеющими любой знак. С каждым таким рядом

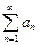(1)

связан ряд с неотрицательными членами, составленный из модулей членов данного ряда, т.е. ряд

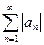(2)

Определение. Ряд (1) называется абсолютно сходящимся, если ряд (2) сходится. Если же ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.

Теорема 1. Если ряд сходится абсолютно, то он сходится.

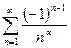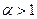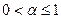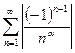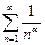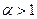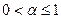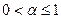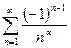Пример 9. Ряд абсолютно сходится при (см. пример 7). Этот ряд сходится условно при . Действительно, ряд = сходится при и расходится при как доказано в примере 7. Однако при ряд сходится по признаку Лейбница.

Дата добавления: 2014-01-07