Интегрируемые типы ДУ второго порядка

Дифференциальные уравнения второго порядка

Интегрируемые типы ДУ второго порядка. Случаи понижения порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Общий вид ДУ второго порядка

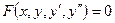
Общее решение 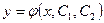этого уравнения содержит две независимые произвольные постоянные и 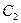. Если заданы начальные условия , 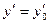при 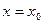, то из системы

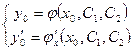
можно, вообще говоря определить постоянные и 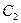и найти тем самым частное решение данного уравнения, удовлетворяющее начальным уравнениям.

Рассмотрим некоторые случаи, когда уравнение второго порядка решается применением операций неопределённого интегрирования.

1.1. Пусть

Интегрируя, получим

.

Интегрируя ещё раз, получим

,

где и 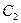- произвольные постоянные.

Пример 1. Найти частное решение ДУ 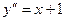, удовлетворяющее начальным условиям , .

Решение. Интегрируем обе части дважды:

,

,

,

.

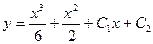Получим общее решение данного ДУ. Находим частное решение, удовлетворяющее начальным условиям:

, , .

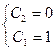1.2. Пусть . Положим 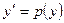. Тогда .

Следовательно, исходное уравнение принимает вид .

Разделяя переменные, получим .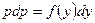

Интегрируя последнее уравнение, находим

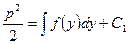
или

,

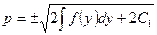Разделим переменные

.

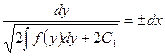Тогда

.

Пример 2. Решить уравнение .

Решение. Полагаем 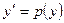. Тогда .

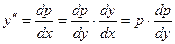Подставляя в уравнение, имеем

.

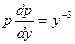Разделяя переменные и интегрируя, получим

,

откуда ,

,

.

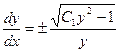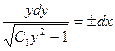Умножим обе части на и проинтегрируем их

,

,

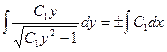откуда

.

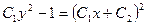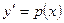1.3. Пусть . Полагаем . Тогда 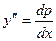и данное уравнение принимает вид .

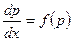Разделяя переменные и интегрируя, последовательно будем иметь

,

.

Определив из этого уравнения величину 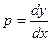, путём вторичного интегрирования можно найти и .

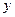Пример 3. Найти решение уравнения 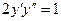, удовлетворяющее начальным условиям , .

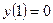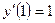Решение. Полагаем 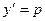и 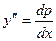. Тогда , откуда , .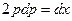

Используя начальное условие 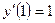, имеем 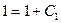, откуда .

Следовательно, . Тогда 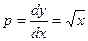, причём перед корнем взят знак «+», т.к. при 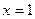мы должны иметь .

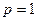Разделяя переменные и интегрируя, находим

.

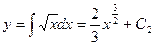Т.к. 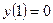, то 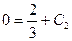, откуда .

Таким образом, искомое решение есть

.

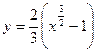Дата добавления: 2014-01-07