Концентрация электронов и дырок в зонах для различных степеней вырождения электронного или дырочного газа

Распределение электронов и дырок по квантовым состояниям в главных энергетических зонах кристалла. Уровень Ферми. Поверхность Ферми. Плотность квантовых состояний для энергетических зон с изотропным и анизотропным законом дисперсии.

Для определения s твердого тела необходимо знать равновесную (темновую) концентрацию электронов (n) и дырок (p).

Для определения n и p необходимо знать параметры зон – плотность квантовых состояний и вероятность их дополнения – функцию распределения электронов и h⁺ по состояниям.

Функции распределения электронов и дырок по квантовым состояниям разрешения зон (зона проводимости и валентная зона).

Электроны в металлах, полупроводниках подчиняются квантовой статистике. Вероятность заполнения уровня E при температуре T определяется функцией Ферми – Дирака: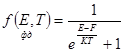

Электроны проводимости – фермионы – частицы, обладающие полуцелым спином, и подчиняются принципом Паули:

F – уровень (энергия) Ферми, или электрохимический потенциал.

Основные свойства функции f_Ф-Д :

При T ® 0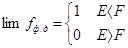

При T = 0 функция терпит разрыв (то есть функция не определена).

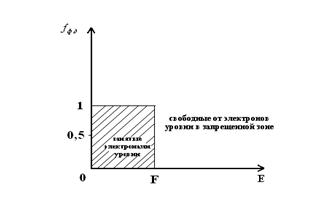
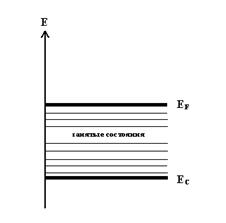
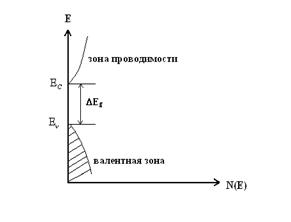
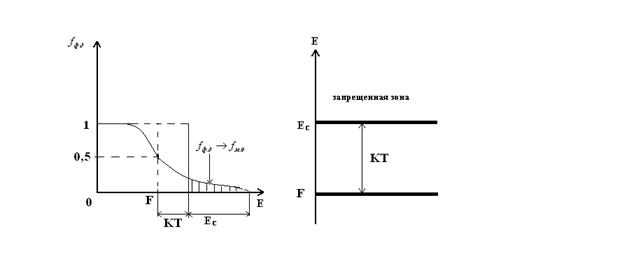
Из графика следует, что f есть уровень, который разделяет занятые электронами состояния в зоне проводимости от свободных.

В металлах при T = 0: уровень F соответствует максимальной энергии электронов в зоне проводимости – энергии Ферми.

В - пространстве вводят

поверхность Ферми,

которая соответствует энергии E_F.

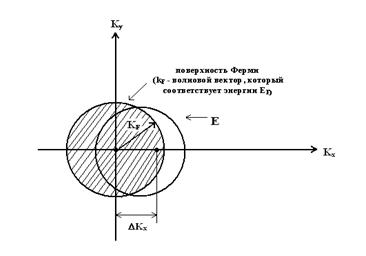
Внутри сферы Ф – находятся электроны проводимости.

Проводимость по зоне проводимости - есть жесткое смещение сферы Ф в - пространстве под действием внешнего электрического поля на величину Dk_x.

При температурах T > 0:

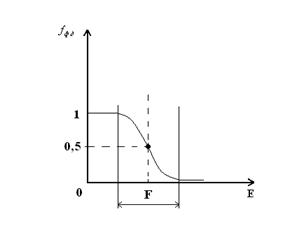
f_Ф-Д = 0,5 и F имеет смысл уровня, вероятность заполнения которого ½.

Функция f_Ф-Д претерпевает наибольшее изменение для энергий вблизи F.

При (E – F) >> kT функция f_Ф-Д переходит в классическую функцию Максвелла – Больцмана:

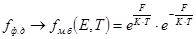– это высокоэнергетический хвост функции f_Ф-Д.

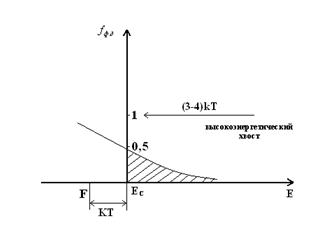
Уровень F ниже Ec на энергию не меньше kT.

В этом случае действует классическая статистика Максвелла – Больцмана и полупроводников, подчиняющиеся этой статистике – невырожденные (по концентрации).

Невырожденный полупроводник n-типа – полупроводник, в котором уровень F лежит ниже Ec в запрещенной зоне на величину не меньше kT.

Таким образом, в невырожденном полупроводнике на уровне f – нет электронов в отличие от металла!

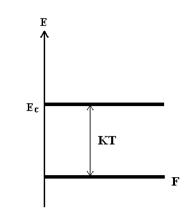
Невырожденный полупроводник p-типа – уровень F лежит выше Ec на величину kT.

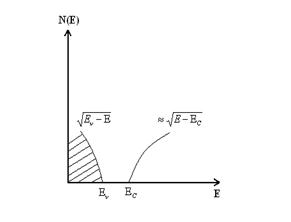
Плотность состояний N(E)

- это число квантовых состояний в зоне, приходящихся на единичный интервал энергии в кристалле единичного объема.

Предположим, что в интервале энергии: (E,E + dE) находится dS состояний.

Тогда для кристалла единичного объема: dS = N(E)dE пропорционально dE

N(E) = dS/dE – плотность состояний.

N(E) связана с формой поверхности равной энергии.

Интервалу dE соответствует шаровой слой объема, которым выделяют поверхности равной энергии:

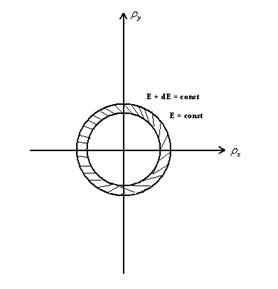E, E + dE = const

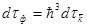
Число состояний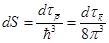

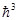- объем, приходящий на одно состояние.

Плотность состояний в зоне проводимости

Эффективная масса – скалярная величина m_n

N(E) = dS/dE dS – число состояний в интервале E, E + dE в кристалле единичного объема.

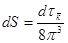
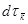- элемент объема 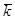- пространства, заключается между поверхностями равной энергии.

E = const и E +dE = const

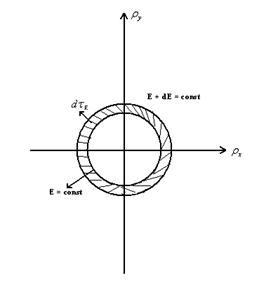
Найдем 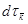, используя закон дисперсии для полупроводника с изотропной эффективной массой электрона m_n

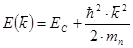
Поверхности E, E + dE заключают объем 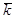- пространства

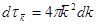
(поверхности – сферы; 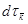- шаровой слой)

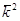- найдем из закона дисперсии:

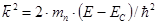
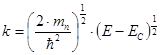
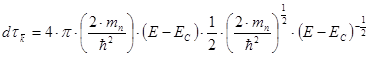
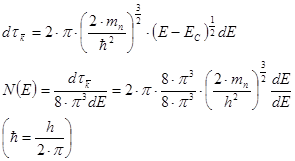
Таким образом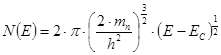

Для изотропной валентной зоны: (m_p – эффективная масса дырки)

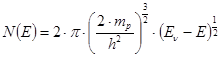
Таким образом, плотность состояний пропорциональна:

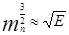
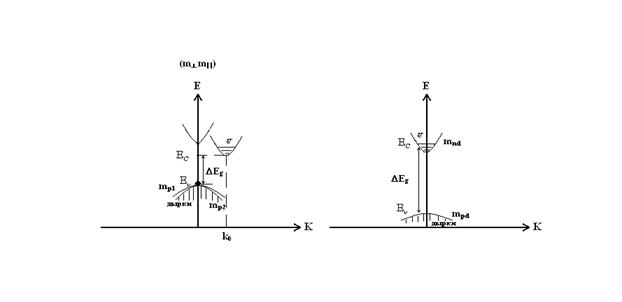
Зонная модель прямозонного полупроводника с использованием функций N(E)

Используется в физике полупроводниковых приборов.

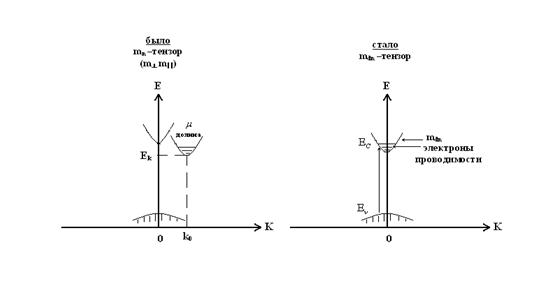
Плотность состояний в зоне проводимости многодолинного (непрямозонного) полупроводника

Эффективная масса m_n - тензорная величина.

Закон дисперсии - анизотропная квадратичная величина:

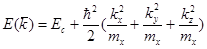
m_C^-1, m_U^-1, m_Z^-1 – компоненты эффективной массы.

Поверхности равной энергии – эллипсоидальные с полуосями.

a, b, c: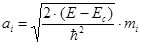

(j = x, y, z)

Объем эллипсоида: V = 4/3p * a b c

Объем, которым выделяют поверхности E и E + dE = const находят как приращение объема dV.

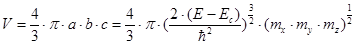
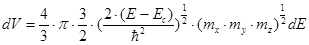
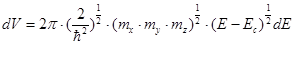
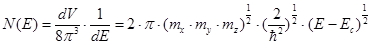
Таким образом, для одной долины:

N(E) = 2p (m_x m_y m_z)^1/2 (2/h)^3/2 (E – Ec)^1/2

Для m-долин:

N(E) =m * 2p (m_x m_y m_z)^1/2 (2/h²)^3/2 (E – Ec)^1/2

Приведем эту формулу к виду для прямозонного полупроводника.

Для этого введем понятие эффективной массы для плотности состояний m_nd:

N(E) = 2p (2 m_nd / h²) ^3/2 (E – Ec)^1/2

где m_nd = m^2/3 (m_x m_y m_z)^1/2

Если поверхности – эллипсоиды вращения (электроны в Ge, Si)

m_x = m_y = m_^, m_z =m_ïï

Таким образом, m_nd = m^2/3 (m²_^ m_ïï)^1/2\

m_^ и m_ï½ определяется из эксперимента по циклотронному резонансу.

Смысл введения m_nd

Позволяет многодолинную зону проводимости с анизотропной эффективной массой mn записать параболичной зоной с изотропной массой с одним абсолютным минимумом (нужно для вычисления концентраций).

Эффективная масса дырок для плотности состояний - m_pd

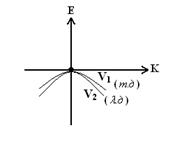вводится для вырожденной валентной зоны (вырождение по энергии)

V₁ и V₂ – стыкуются в точке 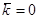- имеют одинаковую энергию, но разные волновые функции.

V₁ – подзона тяжелых дырок с изотропной массой – m_p1

V₂ – подзона легких дырок с эффективной массой – m_p2.

Плотность состояний для валентной зоны:

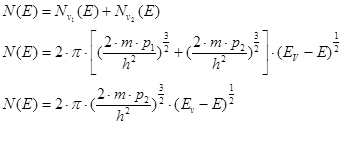
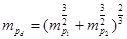
эффективная масса дырок для плотности состояний.

Таким образом, с введением m_pd сложная V-зона заменяется параболичной невырожденной валентной зоной:

Модель полупроводников с m_nd и m_pd:

Концентрация электронов и дырок в условиях равновесия в темноте

Концентрация электронов в зоне проводимости.

В интервале E, E + dE в зоне проводимости кристалла единичного объема содержится d_n-электронов:

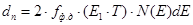
В зоне проводимости: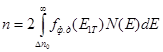

или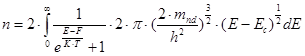

Введем новые переменные:

x= E – Ec/ kT – энергия электронов в единичном kT, отсчитывается от дна Ec.

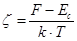- приведенный уровень Ферми

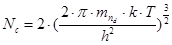– эффективная плотность состояний в зоне проводимости

Тогда 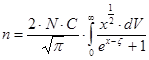- интегралы Ферми: 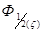от параметра порядка 1/2.

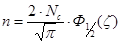- общая формула для любой степени вырождения электронного газа.

Приближенные значения :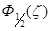

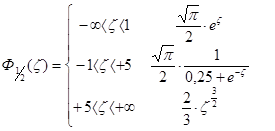невырожденный электронный газ

промежуточный случай

сильновырожденный электронный газ (металлы, вырожденые полупроводники)

Концентрация электронов проводимости в невырожденных полупроводниках

Общая формула: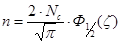

N_C – эффективная плотность состояний в зоне проводимости 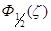- интеграл Ферми.

Рассмотрим: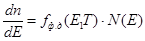

dn – число электронов в интервале E, E + dE зоны проводимости для V = 1

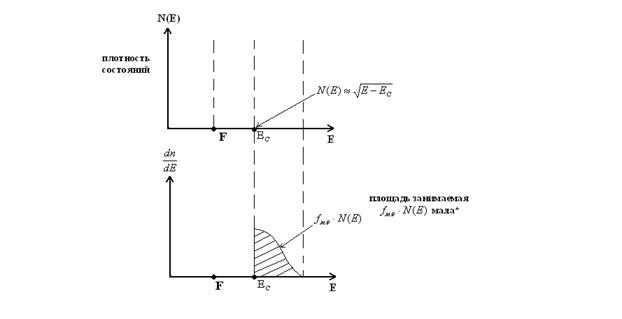
* - это указывает на незначительную концентрацию электронов в зоне проводимости – что характерно для невырожденного полупроводника.

Электроны распределены в узком интервале энергий вблизи дна зоны проводимости.

Определим n:

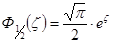
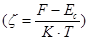
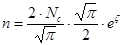
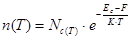– концентрация зависит по экспоненте от T – признак невырожденности электронного газа.

Электропроводность полупроводника так же зависит по экспоненте от T:

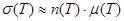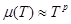(- слабее зависит от T)

Концентрация электронов проводимости в сильновырожденном полупроводнике

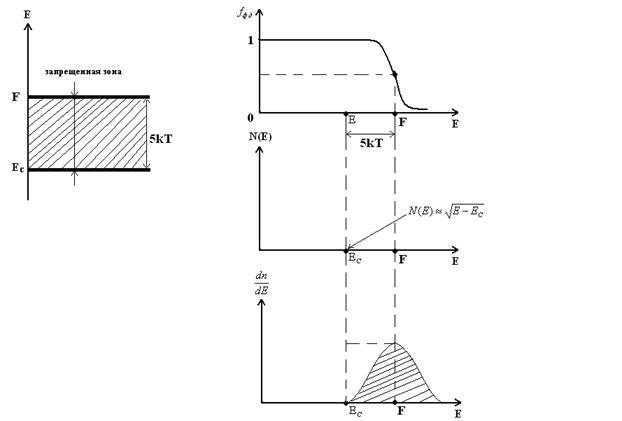
Площадь под кривой значительно больше, чем невырожденности полупроводника, что указывает на большую концентрацию электронов в зоне проводимости.

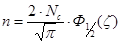, где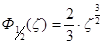

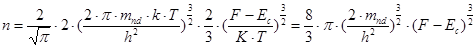
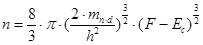
Таким образом, n не зависит от T – признак сильного вырождения электронного газа.

При T = 0 s ¹ 0 (как в металле)

Для промежуточной системы вырождения электронного газа:

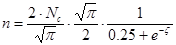
Концентрация дырок в полупроводнике p-типа

Невырожденный дырочный газ (полупроводник):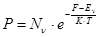

Сильно вырожденный дырочный газ (полупроводник):

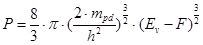
Сильновырожденный полупроводник p-типа:

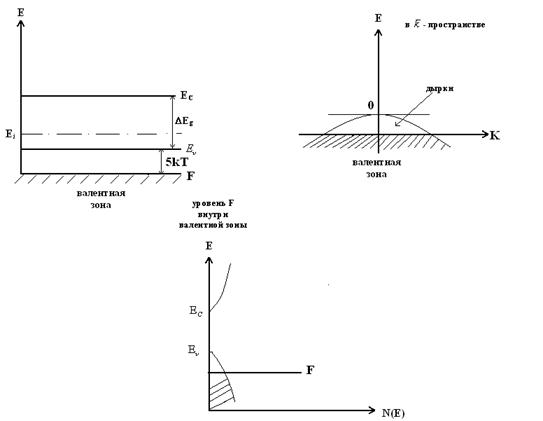
Смысл Nc и Nv в статистике

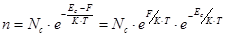
Таким образом, при расчете n в невырожденном полупроводнике n-типа зону проводимости представляют как набор Nc числа уровней с одинаковой энергией Ec.

Nv – валентная зона состоит из Nv уровней с одинаковой энергией Ev.

Уравнение электрической нейтральности для полупроводников и диэлектриков

Для определения n, p необходимо знать положение уравнения Ферми. Его определяют из уравнения электронейтральности полупроводников (диэлектриков).

Смысл уравнения: в любом физически малом объеме полупроводника (диэлектрика) концентрация отрицательно свободных и связанных зарядов = концентрации свободных и связанных зарядов.

Свободные носители - 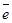и h⁺

Связанные: дырки на уровнях донора – концентрация Pd (D⁺) электроны – акцептора - n_a (A^-).

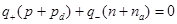
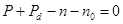
Собственный полупроводник

Уровень Ферми. Собственная концентрация носителей заряда.

Электронные процессы:

G₀ и R₀ – скорости процессов.

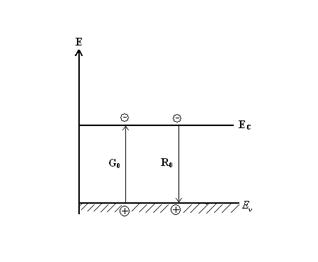
В равновесии G₀ =R_0.

Этому состоянию соответствует равенство n = p = n_i

n_i – собственная концентрация носителей заряда.

G₀ – термическая генерация 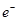и h⁺.

Энергия рекомбинирующих частиц(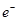+ h⁺) идет на нагрев кристалла (возбуждение определенных типов колебаний кристаллической решетки).

Определение Fi

Уравнение электронейтральности: n = p

Для невырожденных собственных полупроводников: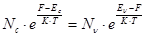

Откуда: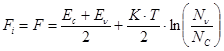

или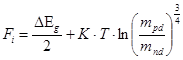

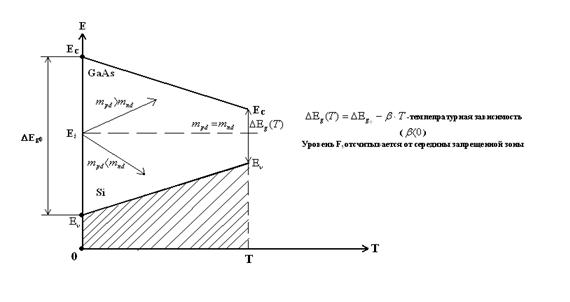
F_i линейно зависит от T.

Собственная концентрация n_i

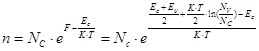откуда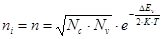

n_i – зависит от DEg, плотности состояний в зонах и температурах:

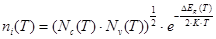
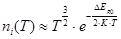
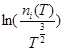линейно зависит от .

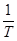Угловой коэффициент ()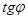

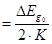
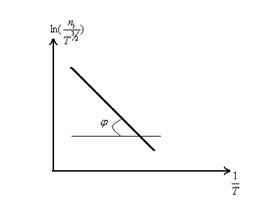
Таким образом, по n_i (T) можно определить DE_g при T = 0 k.

Произведение np в невырожденном полупроводнике

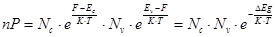- не зависит от положения уровня Ферми в полупроводнике.

Используется для определения концентрации неосновных носителей заряда по известной концентрации основных носителей заряда.

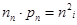· – Закон действующих масс для полупроводников n-типа.

· или 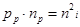– Закон действующих масс для полупроводников p-типа.

Дата добавления: 2014-01-07