Ограниченная взаимная растворимость жидкостей, распределение вещества между двумя жидкими фазами

Если компоненты жидкой смеси очень сильно различаются по своей природе (например, вода-бензол, вода-ртуть и др.), то взаимная растворимость их очень мала. Практически такие жидкости не смешиваются друг с другом. Если к смеси двух несмешивающихся (или ограниченно растворимых друг в друге) жидкостей прибавить некоторое количество вещества, растворимого в обеих жидкостях, то оно распределяется между обоими слоями в определенном отношении. Установлено, что при постоянной температуре третий компонент распределяется между обеими жидкими фазами так, что отношение его концентраций в этих двух фазах сохраняется постоянным. Это положение составляет сущность закона распределения, установленного немецким ученым В. Нернстом в 1890г. и подробно исследованного применительно к различным системам советским ученым Н.А. Шиловым.

Если при 25^оС в систему, состоящую из хлороформа и воды, ввести йод, то отношение равновесных концентраций йода в хлороформе С₁ и воде С₂, или так называемый коэффициент распределения составит:

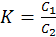(7.3)

Коэффициент распределения зависит от природы веществ, составляющих систему, и температуры.

Закон Нернста – Шилова в форме (7.3) справедлив в тех случаях, когда добавление третьего компонента не вызывает изменения растворимости жидкостей друг в друге, и если третий компонент в каждой из равновесных жидких фаз находится в одинаковом молекулярном состоянии.

Если же вещество, распределяющееся между обеими жидкими фазами, диссоциирует или ассоциирует, то устанавливается сложное равновесие между простыми и ассоциированными молекулами или ионами в пределах каждой фазы и между фазами. Для этого случая закон распределения можно записать:

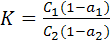(7.4)

где С₁ и С₂ – концентрации растворенного вещества АВ в первой и второй фазах;

а₁ и а₂ – степень диссоциации и ассоциации распределяемого вещества АВ в первой и во второй фазах.

Приводимые выражения справедливы только для разбавленных растворов. Даже для слабых электролитов уже в растворах средней концентрации следует применять активности. При определении распределения сильных электролитов замена активностей концентрациями приводят к неверным результатам.

Опытное значение коэффициентов распределения позволяет определять степень диссоциации или ассоциации растворенного веществ в том или ином растворителе, активности растворенных веществ и т.д.

Знание коэффициента распределения важно и для промышленности при выборе растворителя для процесса экстракции.

Экстрагирование – это извлечение растворенного вещества АВ из раствора соответствующим растворителем, который не смешивается с первым, но в больших количествах растворяет вещество АВ. Обычно этот растворитель подбирают с меньшим удельным весом, чем удельный вес раствора.

Примерами жидкостной экстракции в промышленности могут служить: извлечение йода из водных растворов хлороформом или сероуглеродом; получение концентрированной уксусной кислоты из ее разбавленных растворов путем экстрагирования этилацетатом с последующей перегонкой; отделение пенициллина и других антибиотиков от ферментационных растворов.

Для более полной экстракции вещества необходимо переводить его в то молекулярное состояние, в котором оно находится в обоих растворителях. Например, при извлечении органической кислоты из водных растворов необходимо подавить ее диссоциацию добавлением сильной минеральной кислоты, тогда молекулы органической кислоты экстрагируются более полно и т.д.

При экстракции коэффициентом распределения условились называть отношение концентрации раствора, из которого экстрагируется растворенное вещество, к концентрации раствора, которым производится экстрагирование. Например, коэффициент распределения йода между водой и сероуглеродом равен: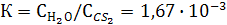

Закон Нернста – Шилова показывает, что экстракцию выгоднее проводить не сразу всем объемом растворителя, а последовательным многократным экстрагированием несколькими порциями растворителя.

Пусть V₁ – объем раствора, содержащего определенное количество g₀ растворенного вещества, которое надо экстрагировать при помощи второго растворителя, не смешивающегося с первым; V₂ – объем растворителя, употребляемый на каждое экстрагирование.

Предположим, что после первого экстрагирования в исходном растворе останется g₁ растворенного вещества, тогда количество экстрагированного вещества, заключенного в объеме V₂, равно .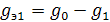

Если экстрагируемое вещество не диссоциирует и не ассоциирует ни в одном из растворителей, то равновесные концентрации его в первом и втором растворителях будут:

.

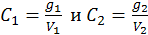Согласно закону распределения имеем:

,

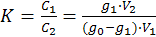откуда

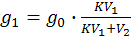(7.5)

Если после отделения раствора от растворителя снова повторить экстрагирование, добавив тот же объем V₂ растворителя, то в него экстрагируется 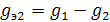, где g₂ – количество вещества, оставшееся после второй экстракции в растворе.

Тогда после второго экстрагирования имеем:

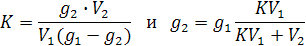
Если вместо g₁ подставить его значение из уравнения, получим:

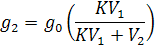
После n – экстрагирований в исходном растворе останется:

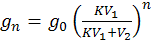(7.6)

Количество экстрагированного вещества определяется выражением:

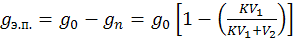(7.7)

Так как 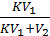< 1, то из соотношения (7.6) вытекает, что чем больше n, т.е. число экстрагирований, тем меньше количество вещества, остающегося в растворе g_n.

Таким образом, многократное экстрагирование определенным объемом растворителя выгоднее, чем однократная экстракция этим же объемом растворителя. Например, если извлекать сероуглеродом йод, содержащийся в 1 л воды (0,28 г), то после однократной экстракции 25 мл (0,025 л) сероуглерода в воде остается:

,

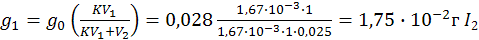что составляет 6,26% исходного количества йода в растворе.

Если тем же объемом СS₂ проводить пятикратную экстракцию, т.е.

V₂ = 5 мл (0,005 л), то количество йода, остающегося в воде будет:

_,

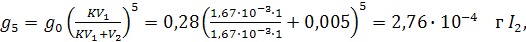что составляет 0,1% исходного количества, т.е. при пятикратной экстракции йод практически полностью извлекается из воды.

Дата добавления: 2014-01-07