Оценка определенных интегралов

Приложения определенного интеграла. Вычисление площади поверхности тела вращения.

Приложения определенного интеграла. Вычисление длины дуги плоской кривой.

Пусть в прямоугольных координатах на плоскости дана кривая y=f(x).

Найдем длину дуги АВ, заключенную, между вертикальными прямыми x=a и x=b. Длиной дуги АВ(s) называется тот предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена стремится к нулю.

Рис. 2. 52.

.

Введем обозначение 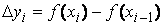, тогда

,

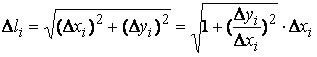или перехода к пределу и суммируя длины, получаем

. (2-147)

Это и есть формула, для расчета длины дуги.

рассмотрим линию в плоскости 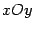, представленную как график функции на отрезке оси 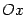. Предположим, что функция имеет на отрезке непрерывную производную .

Пусть поверхность 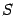получена как результат вращения в пространстве 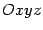линии вокруг оси 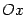(см. рис.). Наша цель -- найти площадь поверхности вращения 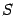(сделанное построение и полученная при этом формула будут одновременно служить и определением того, что такое площадь поверхности ).

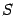Рис.6.19.

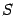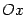Пусть -- площадь той части поверхности , что проектируется на отрезок , лежащий на оси . Очевидно тогда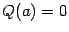, что и что 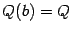-- это искомая площадь.

Найдём производную функции , применив для этого определение производной. Придадим значению переменной некоторое приращение и рассмотрим приращение функции 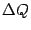. Это приращение равно площади части поверхности 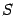между сечениями этой поверхности плоскостями и (если 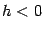, то нужно вдобавок поменять знак). Далее для простоты выкладок будем предполагать 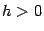. 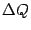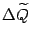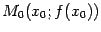Приближённо заменим площадь на площадь боковой поверхности усечённого конуса, образующей которого служит хорда графика , соединяющая точки и 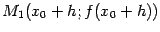в плоскости .

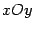Рис.6.20.

Тогда

где 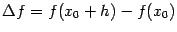и (мы применили к разности 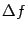, стоящей под знаком корня, теорему Лагранжа).

Запишем теперь 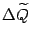в виде

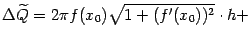
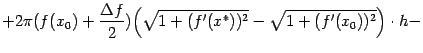
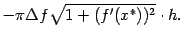
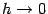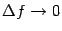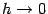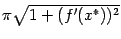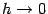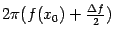Во второй и третьей строках этой формулы бесконечно малыми более высокого порядка малости (при ), чем . Действительно, при , а величина ограничена в силу непрерывности функции и её производной . Далее, из непрерывности следует, что при , а из непрерывности -- что величина ограничена. Следовательно, слагаемое в первой строке формулы -- это главная, линейная по , часть приращения 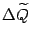, и вместе с ним -- главная часть приращения функции . Напомним теперь, что главная, линейная по часть приращения функции -- это её дифференциал. Значит,

Сменив обозначение на (ведь -- произвольная точка ) и на 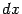, получаем:

Отсюда

С учётом того, что, как мы отмечали выше, 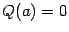, получаем:

Наконец, положив равным , находим искомую площадь поверхности вращения:

(6.10)

(мы снова использовали как обозначение переменной интегрирования).

Дата добавления: 2014-01-07