
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модель на основе временной зависимости затрат ресурсов на НИР и ОКР
|
|
|
|
Пусть в период t в подразделении выполняются НИР в объеме 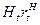 , где Ht - число выполняемых НИР,
, где Ht - число выполняемых НИР, 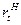 - средние затраты на одну НИР. Тогда на ОКР в этом же периоде остается
- средние затраты на одну НИР. Тогда на ОКР в этом же периоде остается 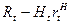 ресурсов, где
ресурсов, где 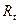 – ресурсы подразделения в период t. Если
– ресурсы подразделения в период t. Если 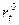 - средние затраты на одну ОКР в единицу времени, то в период t в подразделении могут выполняться работы в среднем по
- средние затраты на одну ОКР в единицу времени, то в период t в подразделении могут выполняться работы в среднем по  ОКР.
ОКР.
Если в одном и том же подразделении предприятия выполняются и НИР и ОКР, то, очевидно, что чем больше было затрачено ресурсов на отработку макетных и экспериментальных образцов в процессе НИР, тем меньше потребуется ресурсов на отработку опытных образцов при выполнении ОКР. Это влияние НИР на ОКР может проявляться, вообще говоря, не сразу, а спустя некоторый период, определяемый продолжительностью выполнения соответствующих этапов ОКР в других подразделениях - соисполнителях этих ОКР.
Таким образом, величина 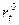 есть некоторая функция затрат ресурсов, выделенных на НИР k периодов назад, т.е.
есть некоторая функция затрат ресурсов, выделенных на НИР k периодов назад, т.е.
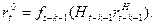 (1)
(1)
Исходя из характера принимаемого во внимание влияния НИР на ОКР, можно предположить, что эта функция представляет собой перевернутую S- образную кривую. С достаточной для практики точностью можно аппроксимировать эту функцию перевернутой логистической кривой (рис. 1).
Считая, что число выполняемых в каждом периоде НИР известно (оно обычно мало меняется от периода к периоду), задачу распределения ресурсов между НИР и ОКР можно теперь сформулировать следующим образом:
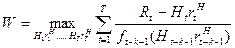 ; (2)
; (2)
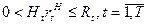 (3)
(3)
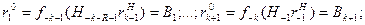 (4)
(4)
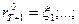
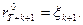 (5)
(5)
Максимизируемый функционал (2) представляет собой среднее количество ОКР, выполненных за Т периодов, где Т- рассматриваемый плановый горизонт. В качестве управляемых переменных выступают затраты на НИР 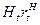 в периоды t=1,2,..., Т. Условие (3) означает, что в любой период t суммарные затраты на НИР не могут превзойти ресурсные возможности подразделения. Условие (4) означает, что известны затраты ресурсов на НИР в периоды, отстоящие от исходного (t=l) на 1,2,..., (k+1) интервалов времени назад. Наконец, условие (5) означает, что известны средние затраты ресурсов на одну ОКР в периоды T+1, Т+2, T+k+1. Знание их необходимо для того, чтобы ограничить нижний предел величины НtrtH для t = T-k,..., T. Из (2) непосредственно следует, что при отсутствии условий (5) значения НtrtH для t = T-k, …, Т, оптимизирующие (2), равны 0, т.е. в эти периоды не будут совсем проводиться НИР.
в периоды t=1,2,..., Т. Условие (3) означает, что в любой период t суммарные затраты на НИР не могут превзойти ресурсные возможности подразделения. Условие (4) означает, что известны затраты ресурсов на НИР в периоды, отстоящие от исходного (t=l) на 1,2,..., (k+1) интервалов времени назад. Наконец, условие (5) означает, что известны средние затраты ресурсов на одну ОКР в периоды T+1, Т+2, T+k+1. Знание их необходимо для того, чтобы ограничить нижний предел величины НtrtH для t = T-k,..., T. Из (2) непосредственно следует, что при отсутствии условий (5) значения НtrtH для t = T-k, …, Т, оптимизирующие (2), равны 0, т.е. в эти периоды не будут совсем проводиться НИР.
Для заданного планового горизонта можно произвольно выбирать значения НtrtH только для первых (Т - k - 1) периодов, так как значения НtrtH для остальных (k+ 1) периодов определены условиями (5). Эти НtrtH изменяют значения средних затрат на одну ОКР для последних (T - k - 1) периодов, так как значения средних затрат на одну ОКР для первых (k+ 1) периодов определены условиями (4). Поэтому задача (2)-(5) имеет нетривиальное решение только для Т > k + 1.
При построении рекуррентного соотношения используем метод математической индукции.
Обозначим через 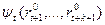 максимально возможное среднее количество ОКР, которое можно выполнить за t периодов при условии, что в (t + l), (t + 2), …, (t + k + 1) периодах будет создан научно-технический задел, обеспечивающий возможность выполнения ОКР в эти периоды со средними затратами ресурсов, соответственно равными
максимально возможное среднее количество ОКР, которое можно выполнить за t периодов при условии, что в (t + l), (t + 2), …, (t + k + 1) периодах будет создан научно-технический задел, обеспечивающий возможность выполнения ОКР в эти периоды со средними затратами ресурсов, соответственно равными 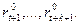
Очевидно, что для t=k+ 1 функция 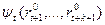 определяется следующим образом:
определяется следующим образом:
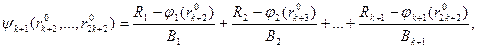 (6)
(6)
где jk+1(…) - функция, обратная (1).
Для t=k+2 эта функция имеет вид
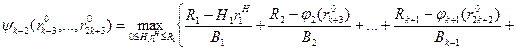
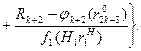 (7)
(7)
Сравнивая выражения (6) и (7), замечаем, что в них второе, третье и т.д. до (k+ 1)-го слагаемые совпадают. Если в (6) положить 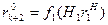 , то и первые слагаемые в (6) и (7) совпадут, так как
, то и первые слагаемые в (6) и (7) совпадут, так как 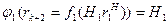 .
.
Отсюда следует, что
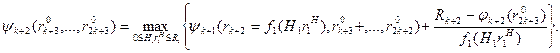 (8)
(8)
Рассуждая аналогично, по методу математической индукции можно доказать, что для любого t (k+ 1 <t£ Т) справедливо следующее рекуррентное соотношение:
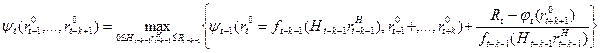 (9)
(9)
Задачу (2) - (5) можно решить теперь следующим образом. Используя формулу (6), вычисляем функции 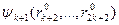 для всех значений
для всех значений 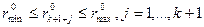 , определенных с заданной дискретностью. После этого, используя формулу (8), а затем последовательно формулу (9), вычисляем значения функций
, определенных с заданной дискретностью. После этого, используя формулу (8), а затем последовательно формулу (9), вычисляем значения функций 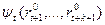 , полагая t = k +2,…, T -1, T. Для каждого набора переменных
, полагая t = k +2,…, T -1, T. Для каждого набора переменных 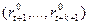 фиксируем значение
фиксируем значение 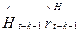 , при котором достигается максимум в выражении (9). Полагая в функции
, при котором достигается максимум в выражении (9). Полагая в функции 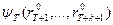 значения переменных равными соответственно
значения переменных равными соответственно 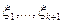 , находим решение задачи (2) - (5) и искомое значение
, находим решение задачи (2) - (5) и искомое значение 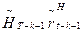 , при котором достигается максимум выражения (9). После этого вычисляем значение
, при котором достигается максимум выражения (9). После этого вычисляем значение 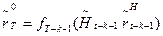 . По набору переменных
. По набору переменных 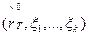 в таблице, определяющей функцию
в таблице, определяющей функцию 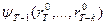 , находим соответствующее значение
, находим соответствующее значение 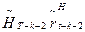 . Затем вычисляем
. Затем вычисляем 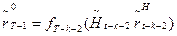 и в таблице, определяющей функцию
и в таблице, определяющей функцию 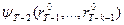 , находим соответствующее значение
, находим соответствующее значение 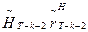 , и т.д. до тех пор, пока не дойдем до
, и т.д. до тех пор, пока не дойдем до 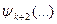 и не получим значение
и не получим значение 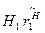 .
.
В результате описанной процедуры получаем искомые значения 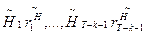 для первых (T - k -1) периодов. Остальные значения
для первых (T - k -1) периодов. Остальные значения 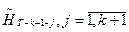 вычисляются путем решения уравнений
вычисляются путем решения уравнений 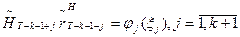 , где xj определяются условием (5).
, где xj определяются условием (5).
Лекция 19.
5.2. Модели этапа исходного планирования разработок
5.2.1. Модель оценки технического уровня предстоящей разработки
Технический уровень изделия – это относительная характеристика качества этого изделия, основанная на сопоставлении значений показателей (параметров), характеризующих техническое и эргономическое совершенство оцениваемого изделия с соответствующими базовыми (эталонными) изделиями.
В процессе определения критерия оценки технического уровня учитывают влияние не одного какого-либо параметра, а совокупность нескольких основных, важнейших параметров, так как улучшение одного из них может привести к ухудшению другого, что в итоге может привести к изменению значения выбранного критерия.
Перечень таких параметров, как правило, устанавливает разработчик изделия, возможно совестно с другими заинтересованными организациями. При этом, очевидно, каждый параметр следует выбирать таким образом, чтобы с его увеличением значение критерия увеличивалось бы.
Всю совокупность выбранных параметров рассматриваемого изделия представим в виде вектора
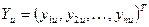 , (1)
, (1)
где 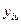 - значения параметра
- значения параметра 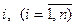 для изделия
для изделия 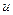 .
.
Составим следующую матрицу значений параметров группы из 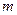 аналогичных изделий, которая характеризует достигнутый отечественный или мировой уровень аналогичных изделий:
аналогичных изделий, которая характеризует достигнутый отечественный или мировой уровень аналогичных изделий:
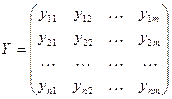 . (2)
. (2)
Переходя к лучшим значениям параметров в выражении (2), получим вектор
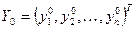 , (3)
, (3)
где 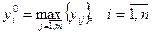 .
.
Вектор 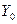 характеризует технический уровень некоторого идеального, эталонного изделия.
характеризует технический уровень некоторого идеального, эталонного изделия.
Обобщенный показатель технического уровня исследуемого изделия 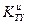 можно теперь определить следующим образом:
можно теперь определить следующим образом:
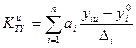 , (4)
, (4)
где:
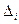 - предельное отклонение
- предельное отклонение 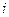 -го параметра, т.е. разность между наибольшим и наименьшим значениями
-го параметра, т.е. разность между наибольшим и наименьшим значениями 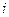 -го параметра, взятыми по всей совокупности параметров изделий, включая и рассматриваемое изделие. Если
-го параметра, взятыми по всей совокупности параметров изделий, включая и рассматриваемое изделие. Если 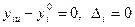 , то
, то 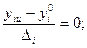
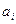 - весовой коэффициент, отражающий неравнозначность вклада отдельных параметров в оценку технического уровня изделия. Полагают, что
- весовой коэффициент, отражающий неравнозначность вклада отдельных параметров в оценку технического уровня изделия. Полагают, что 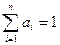 .
.
Если подсчитанный по формуле (4) показатель 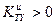 , то это означает, что технический уровень оцениваемого изделия выше технического уровня аналогичных изделий взятых для сравнения. Если же
, то это означает, что технический уровень оцениваемого изделия выше технического уровня аналогичных изделий взятых для сравнения. Если же 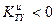 , то это означает, что технический уровень оцениваемого изделия ниже технического уровня аналогов.
, то это означает, что технический уровень оцениваемого изделия ниже технического уровня аналогов.
В формуле (4) неизвестными являются численные значения весовых коэффициентов 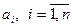 .
.
Для их определения может быть применен метод парных сравнений. Его сущность состоит в том, что каждому эксперту, выбранному для определения важности отдельных показателей в итоговой оценке технического уровня изделия, предлагается сравнивать относительную важность пар различных параметров. Для этого составляют квадратные матрицы парных сравнений, в которых все параметры записываются в одном и том же порядке дважды: в верхней строке и в крайнем левом столбце каждой матрицы. В клетках на пересечении 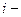 й строки и
й строки и 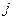 -го столбца
-го столбца 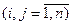 каждый эксперт проставляет числа
каждый эксперт проставляет числа 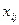 по следующим правилам:
по следующим правилам:
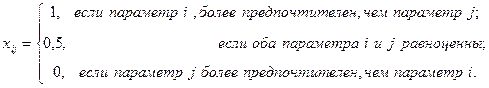
Каждая пара параметров может сравниваться дважды или только один раз. Последний вариант встречается на практике, поэтому его и рассмотрим. Он предполагает, что справедливо следующее очевидное равенство: 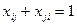 .
.
Полученную от эксперта с номером 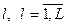 матрицу парных сравнений обозначим
матрицу парных сравнений обозначим  .
.
Значения весовых коэффициентов 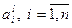 параметров в формуле (4) для эксперта с номером
параметров в формуле (4) для эксперта с номером 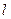 найдем на основе обработки полученной матрицы
найдем на основе обработки полученной матрицы  , воспользовавшись решением так называемой задачи о лидере.
, воспользовавшись решением так называемой задачи о лидере.
Обозначим 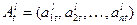 вектор весовых коэффициентов параметров для эксперта с номером
вектор весовых коэффициентов параметров для эксперта с номером 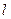 , полученный на шаге вычислений
, полученный на шаге вычислений 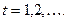
Для вычисления компонент этого вектора воспользуемся следующей формулой:
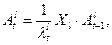 (5)
(5)
где величина 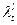 определяется по следующей формуле:
определяется по следующей формуле:
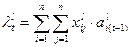 . (6)
. (6)
На первом шаге вычислений полагают все элементы вектора 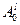 равными единице.
равными единице.
По определению, матрица  неотрицательная. Поэтому согласно теореме Перрона – Фробениуса при стремлении числа шагов вычислений
неотрицательная. Поэтому согласно теореме Перрона – Фробениуса при стремлении числа шагов вычислений 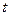 к бесконечности, величина
к бесконечности, величина 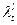 стремится к собственному числу
стремится к собственному числу 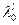 матрицы
матрицы 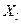 , а вектор весовых коэффициентов
, а вектор весовых коэффициентов 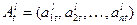 стремится к собственному вектору этой матрицы, соответствующему максимальному собственному числу
стремится к собственному вектору этой матрицы, соответствующему максимальному собственному числу 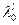 , т.е. можно записать:
, т.е. можно записать:
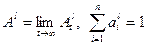 , (7)
, (7)
где 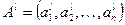 .
.
Таким образом, последовательно применяя формулы (5) и (6), находим 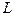 векторов
векторов  , компонентами которых являются весовые коэффициенты параметров в формуле (4).
, компонентами которых являются весовые коэффициенты параметров в формуле (4).
Необходимо теперь установить степень согласованности мнений экспертов относительно полученных значений компонент векторов  .
.
Одним из возможных подходов для определения степени согласованности мнений экспертов является подход, основанный на использовании метода ранговой корреляции и вычислении так называемого коэффициента конкордации W.
Для его вычисления перейдем от значений коэффициентов относительной важности 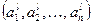 к рангам этих критериев
к рангам этих критериев 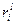 . При этом ранг, равный единице, присваивается параметру, у которого соответствующий ему весовой коэффициент наибольший. Ранги
. При этом ранг, равный единице, присваивается параметру, у которого соответствующий ему весовой коэффициент наибольший. Ранги 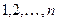 присваиваются параметрам по мере уменьшения их весовых коэффициентов. Ранг
присваиваются параметрам по мере уменьшения их весовых коэффициентов. Ранг 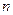 присваивается параметру, имеющему наименьший весовой коэффициент.
присваивается параметру, имеющему наименьший весовой коэффициент.
Коэффициент конкордации W рассчитывается по следующей формуле, которую предложил Кендалл:
 (8)
(8)
где
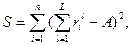 (9)
(9)
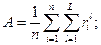 (10)
(10)
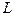 – количество экспертов,
– количество экспертов,
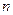 – количество локальных критериев,
– количество локальных критериев,
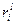 - ранг локального критерия с номером
- ранг локального критерия с номером 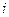
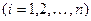 согласно мнению эксперта с номером
согласно мнению эксперта с номером 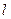
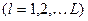 .
.
Коэффициент конкордации W меняется от 0 до 1, причем, если он равен 1, то оценки всех экспертов полностью совпадают; если же он равен 0, то связь между оценками отсутствует.
Если 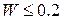 , то согласованность оценивается как низкая; если
, то согласованность оценивается как низкая; если 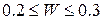 - удовлетворительная и, если
- удовлетворительная и, если 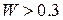 - высокая.
- высокая.
Низкий коэффициент согласованности указывает либо на неудачный выбор ранжируемых факторов, либо на то, что мнения экспертов по данному вопросу резко расходятся. В этом случае необходимо провести новый экспертный опрос, возможно изменив состав экспертов.
Если гипотеза о согласии экспертов принимается, то вычисляются обобщенные итоговые значения весовых коэффициентов относительной важности параметров.
Вначале находим вектор 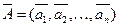
 усредненных по всем экспертам значений весовых коэффициентов параметров в формуле (4).
усредненных по всем экспертам значений весовых коэффициентов параметров в формуле (4).
Величины 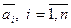 можно вычислить по следующим формулам:
можно вычислить по следующим формулам:
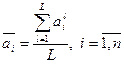 . (11)
. (11)
Формулы (11) предполагает, что все эксперты по своему уровню равноценны, т.е. их мнения равнозначны. Если это не так, т.е. среди экспертов есть специалисты различной квалификации, то вместо формул (11) более целесообразно применить формулы
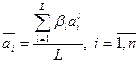 , (12)
, (12)
где 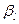 - коэффициент, отражающий степень подготовленности эксперта с номером
- коэффициент, отражающий степень подготовленности эксперта с номером 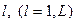 , причем
, причем 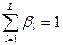 . Для определения значений коэффициентов
. Для определения значений коэффициентов 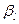 ,
, 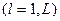 можно применить методику, изложенную выше.
можно применить методику, изложенную выше.
Полученные по формулам (11) или (12) весовые коэффициенты не отвечают условию нормировки, так как в общем случае 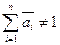 . Поэтому для получения условия нормировки следует перейти от вектора
. Поэтому для получения условия нормировки следует перейти от вектора 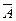 к требуемому вектору параметров
к требуемому вектору параметров 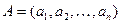 , вычислив значения компонент этого вектора по формулам:
, вычислив значения компонент этого вектора по формулам:
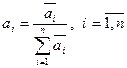 . (13)
. (13)
5.2.2. Модель распределения ресурсов по этапам выполнения разработки
Пусть в результате предварительного исследования технической сущности предстоящей разработки определены основные этапы ее выполнения, число которых обозначим 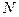 .
.
Нормативную продолжительность выполнения каждого 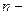 го этапа
го этапа 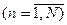 обозначим
обозначим 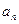 .
.
За счет привлечения дополнительных ресурсов продолжительность этапа 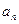 может быть уменьшена на величину не более чем
может быть уменьшена на величину не более чем 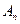 , причем, очевидно,
, причем, очевидно,  .
.
Если нормативная продолжительность этапа 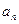 уменьшена на величину
уменьшена на величину 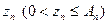 , то его стоимость увеличивается на величину
, то его стоимость увеличивается на величину 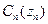 , где
, где 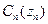 - известная возрастающая функция аргумента. Таким образом, стоимость выполнения
- известная возрастающая функция аргумента. Таким образом, стоимость выполнения 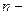 го этапа
го этапа 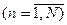 равна
равна 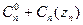 , где
, где 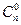 - стоимость этапа при его нормативной продолжительности
- стоимость этапа при его нормативной продолжительности 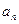 .
.
Превышение заданного срока выполнения разработки на величину 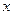 может привести к экономическим санкциям в виде штрафа в размере
может привести к экономическим санкциям в виде штрафа в размере 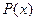 .
.
Одновременно, досрочное выполнение разработки может быть связано с сокращением продолжительности выполнения отдельных этапов и, значит, их удорожанием, а, кроме того, может привести к экономическим потерям из-за необходимости хранения готовой продукции на складе, отвлечения разработчиков от выполнения других разработок и т.п. Эти потери обозначим 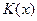 , где
, где 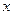 - время «пролеживания» результатов выполнения разработки.
- время «пролеживания» результатов выполнения разработки.
Исходя из сказанного, ожидаемая стоимость выполнения разработки 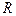 может быть определена следующим образом:
может быть определена следующим образом:
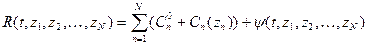 , (1)
, (1)
где 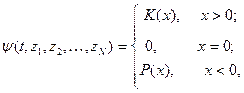
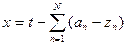 - величина запаздывания или опережения заданного срока выполнения разработки;
- величина запаздывания или опережения заданного срока выполнения разработки;
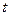 - интервал времени между началом выполнения разработки и требуемым (директивным) сроком ее завершения.
- интервал времени между началом выполнения разработки и требуемым (директивным) сроком ее завершения.
Задача состоит в том, чтобы при заданном 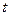 найти такие значения величин
найти такие значения величин 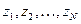 , которые минимизировали бы ожидаемую стоимость выполнения разработки.
, которые минимизировали бы ожидаемую стоимость выполнения разработки.
Решение поставленной задачи можно найти, построив динамическую оптимизационную модель.
Занумеруем все этапы разработки в обратном порядке, так что номер 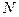 получит первый этап, номер
получит первый этап, номер 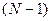 - второй этап и т.д.
- второй этап и т.д.
Пусть после завершения 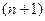 -го этапа осталось
-го этапа осталось 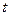 единиц времени до установленного срока окончания разработки. Тогда величина
единиц времени до установленного срока окончания разработки. Тогда величина 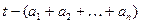 - это время, которое можно потратить на устранение различного рода задержек в выполнении оставшихся этапов. Обозначим эту величину
- это время, которое можно потратить на устранение различного рода задержек в выполнении оставшихся этапов. Обозначим эту величину 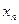 .
.
Перед началом выполнения 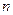 -го этапа величина
-го этапа величина 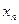 может быть увеличена на
может быть увеличена на 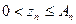 , а в процессе выполнения за счет различных случайных факторов уменьшена в среднем на величину
, а в процессе выполнения за счет различных случайных факторов уменьшена в среднем на величину 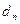 . Поэтому соотношение между величинами
. Поэтому соотношение между величинами 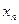 и
и 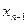 может быть записано в следующем виде:
может быть записано в следующем виде:
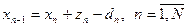 . (2)
. (2)
Очевидно, что при этих обозначениях величина 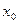 равна неиспользованному резерву времени, если
равна неиспользованному резерву времени, если 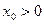 , и нарушению срока выполнения разработки, если
, и нарушению срока выполнения разработки, если  .
.
Предположим, что осталось выполнить самый последний этап с номером 1 и пусть:
- 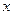 - величина резерва времени (возможно, и отрицательного);
- величина резерва времени (возможно, и отрицательного);
- 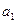 - нормальная продолжительность выполнения этого этапа;
- нормальная продолжительность выполнения этого этапа;
- 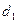 - величина, на которую в среднем удлиняется продолжительность этапа за счет случайных факторов;
- величина, на которую в среднем удлиняется продолжительность этапа за счет случайных факторов;
- 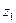 - выбираемая величина, на которую сокращается продолжительность выполнения этапа.
- выбираемая величина, на которую сокращается продолжительность выполнения этапа.
При этих обозначениях величина запаздывания или опережения заданного срока выполнения разработки 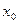 определяется, согласно формуле (2) следующим образом:
определяется, согласно формуле (2) следующим образом:
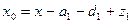 .
.
Найдем минимальные дополнительные затраты на выполнение данного этапа при известном значении величины 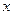 . Они определяются величиной
. Они определяются величиной 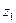 и тем, какого значения при заданных величинах
и тем, какого значения при заданных величинах 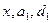 достигла величина
достигла величина 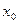 . Эти затраты можно вычислить по следующей формуле:
. Эти затраты можно вычислить по следующей формуле:
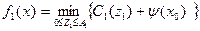 , (3)
, (3)
где 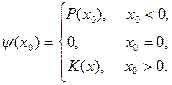
В фигурных скобках выражения (3) первое слагаемое – это затраты на сокращение продолжительности выполнения этапа на величину 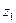 , причем
, причем 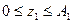 , где
, где 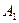 - максимально возможное сокращение продолжительности выполнения этого этапа. Второе слагаемое в фигурных скобках выражения (3) – возможные потери за счет запаздывания срока выполнения разработки, если
- максимально возможное сокращение продолжительности выполнения этого этапа. Второе слагаемое в фигурных скобках выражения (3) – возможные потери за счет запаздывания срока выполнения разработки, если  , или за счет слишком раннего ее окончания, если
, или за счет слишком раннего ее окончания, если 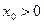 .
.
Пусть теперь осталось выполнить два последних этапа, т.е. первый и второй, причем перед их выполнением имеется резерв времени 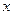 , возможно, и отрицательный. В этом случае величина запаздывания определяется следующим выражением:
, возможно, и отрицательный. В этом случае величина запаздывания определяется следующим выражением:
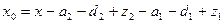 . (4)
. (4)
Найдем минимальные дополнительные затраты на выполнение этих двух этапов при известном значении 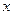 . Они определяются следующей очевидной формулой:
. Они определяются следующей очевидной формулой:
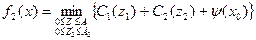 . (5)
. (5)
В выражении (5) величина 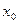 вычисляется уже по формуле (4).
вычисляется уже по формуле (4).
Перепишем выражение (5) в следующем виде:
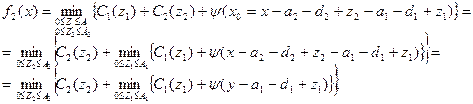 (6)
(6)
где 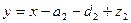 .
.
Из выражений (6) и (3) следует, что выражение (6) можно записать в следующем образом:
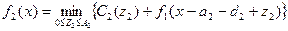 . (7)
. (7)
Рассуждая аналогично, можно получить следующее выражение для минимальных дополнительных затрат на выполнение трех, четырех и т.д. этапов при условии, что перед началом их выполнения имеется положительный или отрицательный резерв времени 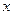 :
:
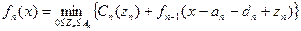 . (8)
. (8)
При построении рекуррентных функций (8) для 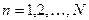 необходимо фиксировать для каждого значения
необходимо фиксировать для каждого значения 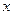 то значение
то значение 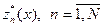 , при котором функционал, стоящий в фигурных скобках в выражении (8), достигает минимального значения. Полученные по рекуррентным формулам (8) функции
, при котором функционал, стоящий в фигурных скобках в выражении (8), достигает минимального значения. Полученные по рекуррентным формулам (8) функции 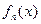 и
и 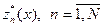 позволяют получить решение поставленной задачи определения значений
позволяют получить решение поставленной задачи определения значений  , которые минимизируют ожидаемые затраты на выполнение разработки при заданной директивной продолжительности ее выполнения
, которые минимизируют ожидаемые затраты на выполнение разработки при заданной директивной продолжительности ее выполнения 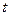 .
.
5.2.3. Сетевые модели выполнения разработок
Одним из широко известных в свое время моделей хода выполнения разработок были так называемые сетевые модели. Эти модели предполагали представление процесса выполнения разработки в виде направленного нагруженного графа, дуги которого – это выполняемые работы (процедуры), а вершины – начало и окончание соответствующих работ (процедур).
Если сетевая модель описывает процесс выполнения какой-то конкретной разработки, то каждая дуга такого графа обычно бывает нагружена наименованием соответствующей работы, продолжительностью выполнения этой работы, видом требуемого для ее выполнения ресурса, в общем случае в виде вектора, и т.д. Кроме того, для каждой вершины графа определены календарные сроки начала или окончания соответствующей работы, для которой эта вершина является либо ее началом, либо ее окончанием. Пример фрагмента такого графа приведен на рис. 1.
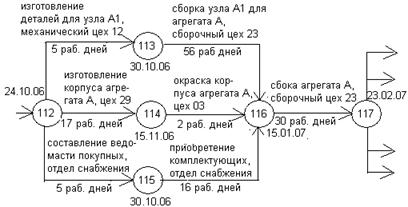
Рис. 1 Фрагмент сетевого графика изготовления агрегата А некоторого изделия
Лекция 20 - 21.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 427; Нарушение авторских прав?; Мы поможем в написании вашей работы!