Динамического программирования

Двухуровневое распределение ресурсов между разработками методом

Процесс решения задачи распределения ресурсов между разработками можно представить как двухуровневую систему принятия решений. Причем на первом уровне мы решаем задачу оптимального распределения ресурсов между отдельными работами данной разработки с целью обеспечения max вероятности ее выполнения, а на следующем уровне решаем аналогичную задачу, но уже для всего множества разработок.

На первом этапе для каждой разработки i =1,2,…,m используется:

1) сетевой график работ по разработке, отражающий последовательность и взаимосвязь выполняемых работ.

2) выделенный обобщенный ресурс: (14)

где j =1,2,…, n_i – число работ i -й разработки

i =1,2,…, m - число разработок.

3) f_ij(q_ij) – вероятность выполнения каждой отдельной работы j разработки i в зависимости от количества выделенного на нее ресурса q_ij. Необходимо определить max общую вероятность выполнения всех работ разработки в заданное время и соответствующее ей распределение обобщенного ресурса между работами, т.е. необходимо решить следующую оптимизационную задачу:

(15)

При условии, что

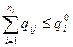(16)

Обычно: 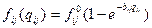(17)

Для решения задачи (15)-(16) воспользуемся методом динамического программирования.

Пусть 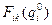– максимальная вероятность выполнения в срок k первых работ i –й разработки при условии, что на нее выделено ресурсов. k =1,2,…, n_i:

…………………………………………

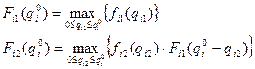
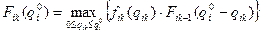(18)

…………………………………………

После построения функций для всех i =1,2,…, m и разных значений решаем задачу второго уровня с целью получения максимальной вероятности выполнения в срок всех разработок тематического плана. Для этого решают задачу:

(19)

При ограничении:

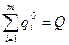(20)

В выражении (19): .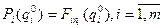

Формально задачи (19)-(20) ничем не отличаются от (15)- (16) и может быть также решения методом динамического программирования. Для этого пусть 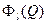есть максимальная вероятность выполнения первых l разработок, l =1,2,…, m.

Тогда имеем:

…………………………………….…..

………………………………………...

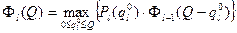
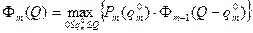
5.3.3. Модель включения в тематический план инициативных разработок

с учетом взаимозаменяемости ресурсов

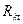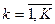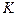После включения в тематический план всех директивных разработок может оказаться, что еще остались ресурсы в количестве , где - номер вида ресурса, , - число различных видов ресурсов, 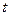- номер периода, , 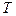- плановый горизонт, на котором решается задача формирования тематического плана.

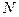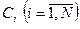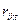
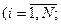
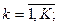
Пусть - число инициативных разработок портфеля заказов. Для каждой такой разработки определены количественная оценка эффективности (важности) , требуемое количество ресурсов , где 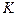- число различных видов ресурсов, 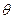- продолжительность выполнения всех инициативных разработок.

Необходимо определить, какие разработки из числа инициативных следует включить в тематический план, обеспечив при этом максимальную суммарную важность всех выбранных разработок с учетом возможности замены одного вида ресурсов другим. Эту задачу можно решить следующим образом.

Назовем вариантом включения разработок в тематический план любое сочетание их из общего списка 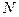конкурирующих разработок. Так как количество вариантов 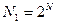, то для представления любого номера 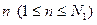в двоичном коде необходимо 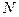двоичных цифр.

Условимся, что каждый разряд двоичного числа соответствует одной разработке, и тогда, если в этом разряде находится 1, то разработка включается в план, если 0 – нет. Таким образом, зная номер варианта, легко определить номера входящих в него разработок, их общую ценность и требуемые ресурсы.

Для осуществления варианта необходимо, чтобы на каждом периоде планирования существовало распределение взаимозаменяемых ресурсов предприятия, удовлетворяющее запросы всех разработок этого варианта. Для определения требований варианта по всем типам ресурсов на каждом периоде планирования просуммируем запросы всех ресурсов.

Для грубой оценки осуществимости варианта можно сравнить сумму его запросов по типам ресурсов на каждом плановом периоде с суммой запасов всех ресурсов предприятия на этом периоде.

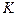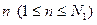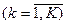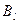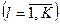Рассмотрим более детально распределение ресурсов на некотором периоде планирования . Пусть имеется всего типов ресурсов; - суммарный запрос всех тем варианта на использование - го типа ресурса ; - величина запасов предприятия по му типу ресурсов ; - объемы 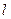-го типа ресурсов, идущие на удовлетворение потребностей варианта в ресурсах - го типа; 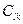- затраты на использование го типа ресурсов вместо - го типа; 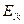- эффективность замены - го типа ресурса м типом, т.е. количество - го типа ресурса, эквивалентное единице го типа ресурса.

При этих обозначениях задача распределения ресурсов состоит в отыскании неотрицательных значений переменных , обеспечивающих минимальные затраты на реализацию варианта при следующих условиях:

- удовлетворение запросов варианта по всем типам ресурсов, т.е.

(1)

- ограниченность ресурсов предприятия, т.е.

(2)

Кроме того, по смыслу задачи

(3)

Критериальная функция модели, минимизирующей общие затраты, имеет следующий вид:

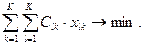(4)

Задача (1) – (4) является задачей линейного программирования, и, в частности, при относится к классу открытых транспортных задач. Ее можно решить известными методами линейного программирования.

В практике тематического планирования РП после включения в план директивных разработок число конкурирующих инициативных разработок обычно невелико, в пределах 10 -12. При большом числе их можно разделить на приоритетные группы важности, актуальности. Поэтому число возможных вариантов включения разработок в тематический план 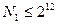, и все эти варианты можно рассмотреть непосредственно и сравнить с помощью ЭВМ.

На этом основан следующий алгоритм направленного перебора формирования тематического плана РП.

1. Для каждого варианта определяется суммарная важность входящих в него вариантов.

2. Все варианты сортируются в порядке убывания их важности. Если все варианты уже просмотрены, то алгоритм заканчивает работу.

3. Последовательно просматриваются все варианты, начиная с первого. Производится грубая оценка осуществимости варианта, затем с помощью решения модели (1) – (4) определяется распределение ограниченных ресурсов РП, удовлетворяющее запросы всех разработок этого варианта. Если такое распределение найдено для всех периодов 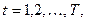то вариант считается оптимальным и входящие в него разработки включаются в тематический план. Если же такого распределения нет или вариант оказывается неосуществимым даже при грубой оценке, то рассматривается следующий вариант из проранжированного по важности списка. Если все варианты просмотрены, то выполняется следующий пункт.

4. В соответствии с ранее рассмотренной в разделе 4.3.1. методикой сроки начала выполнения инициативных разработок, не включенных в план, увеличиваются на один интервал планируемого горизонта, после чего выполняется пункт 2.

Лекция 22 - 23.

Дата добавления: 2014-01-07