Постановка и вероятностная модель определения периодичности контроля процесса выполнения разработок

В процессе оперативного управления разработками возникает задача определения оптимальной периодичности опроса исполнителей с целью контроля за ходом выполнения запланированных им работ. Существуют различные подходы к решению этой задачи.

В [11] предложен метод определения частоты опроса исполнителей при выполнении ими одной достаточно крупной работы. Его особенность состоит в следующем.

1. Чем ближе работа к завершению, тем чаще осуществляется опрос исполнителей, т.е. периодичность контроля за ее выполнением различна.

2. Чем лучше идет работа, тем реже осуществляется ее контроль. Наоборот, при отставании ее выполнения частота контроля увеличивается.

Основными недостатками этого метода являются, во-первых, переменная частота контроля, что усложняет его организацию в АСУ РП, а во-вторых, на некотором шаге контроля, в том числе и первом, результат контроля может быть таким, что даже при принятии оперативных решений выполнить работу в установленный срок из-за большого его отставания окажется уже невозможным. Кроме того, метод предполагает контроль за выполнением только одной работы, что не всегда соответствует реальным процессам проведения разработок в подразделениях РП.

Рассмотрим другой подход к решению задачи определения частоты опроса исполнителей, предполагающий, что за подразделением РП закреплен комплекс запланированных ему работ [12].

Пусть этот комплекс состоит из n работ, для каждой из которых задана ее плановая продолжительность b_r и срок начала выполнения a_r, где . План работы подразделения при этих обозначениях можно представить в виде вектора 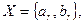r =1, n.

За начальный момент времени t =0 примем момент начала работы подразделения по составленному плану. В случайные последовательные моменты времени t=t₁,t₂,…,t_i,… на подразделение действуют возмущения в виде внеплановых работ, болезней исполнителей, отвлечения исполнителей на выполнение других работ и т.п. Эти возмущения в конечном итоге оказывают влияние на длительность выполнения запланированных работ. Обозначим через Db_r ожидаемое изменение длительности выполнения r -й работы по сравнению с ранее установленной в плане, а через A(t_i)– множество номеров тех работ, для которых в момент t=t_i произошло это изменение.

Ввиду случайности появления возмущающих факторов в момент t_i и их случайного воздействия на длительность выполнения работ из A(t_i) величины 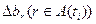будут случайными.

При этих обозначениях величина отклонения фактического хода выполнения от запланированного S(t) в момент времени t>0 может быть определена следующим образом:

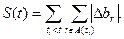(4)

Являясь суммой случайных величин, заданных в случайные момента времени t₁,t₂,…,t_i,<t, эта величина представляет собой дискретный случайный процесс. Обозначим через F(t,y) функцию распределения сечения этого случайного процесса в момент t. Тогда необходимую периодичность контроля за ходом выполнения плана подразделения 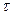можно определить исходя из условия, что в момент времени t=t величина S(t) будет меньше некоторой допустимой величины D, при которой с некоторой заданной вероятностью P^d еще можно путем принятия оперативных решений устранить возникшие отклонения. Это условие записывается следующим образом:

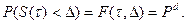(5)

Рассмотрим, как можно найти функцию распределения F(t,y), воспользовавшись рядом оправданных для практики работы РП допущений.

Пусть n(t)– число возмущений, которые действовали на подразделение за время t, а 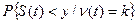– вероятность того, что величина отклонения S(t) в момент t меньше некоторой величины y при условии, что за время t на подразделение действовало ровно k возмущений. По формуле полной вероятности имеем

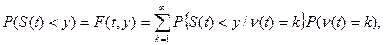(6)

где 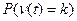– вероятность, что за время t на подразделение действовало ровно k возмущений.

Сделаем следующее допущения:

1. Случайные величины 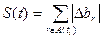независимы, т.е. величина отклонения плана в момент времени t=t_i никак не влияет на величину его отклонения в последующие моменты времени t=t_i1,t_i2,….

2. Случайные величины S(t_i) подчиняются одному и тому же показательному закону распределения с известным параметром a, где 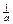– среднее значение величины отклонения хода выполнения плана от номинального значения.

3. Процесс поступления возмущений, влияющих на выполнение плана, - простейший пуассоновский с известным параметром l, где l– среднее число возмущений в единицу времени.

При этих допущениях имеем

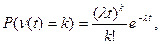(7)

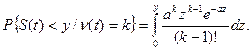(8)

Выражение (8) – это функция распределения случайной величины, полученной путем сложения независимых случайных величин, каждая из которых подчинена показательному закону распределения с параметром a.

Подставляя (7) и (8) в (6), получаем выражение, определяющее функцию F(t,y):

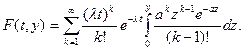(9)

Выражение (9) можно записать в виде [12]

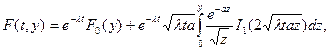(10)

где F₀(y)– вероятность отклонения плана подразделения на величину, не превосходящую при условии, что за время t не действовали никакие возмущения; I₁(u)- функция Бесселя чисто мнимого аргумента первого рода.

Очевидно, что

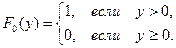(11)

Из выражений (5) и (10) следует, что для нахождения искомой периодичности контроля хода выполнения плана работы подразделения t при известных значениях величин a, t и D необходимо решить следующее выражение:

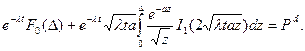(12)

Так как D>0, то, воспользовавшись выражением (11), вместо (12) можно записать следующее:

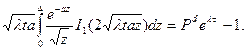(13)

Уравнение (13) можно решить одним из известных численных методов интегрирования.

Дата добавления: 2014-01-07