Оперативном управлении разработками

Графическая модель определения частоты опроса отдельного исполнителя при

При оперативном управлении разработками возникает задача определения оптимальной частоты опроса исполнителей, выполняющих запланированные им работы.

Пусть некоторая работа характеризуется некоторым плановым объемом V_ПЛ, определенным, например, в показателе трудоемкости – человеко-днях. Для этой работы считаются заданными следующие параметры:

1) плановый срок окончания работы t_ПЛ;

2) допустимые пределы отклонения от срока окончания этой работы D t_ПЛ (резерв времени);

3) оптимистический срок окончания работы t₀ при максимальной производительности.

Плановый объем выполняемой работы распределяется в заданном промежутке времени от t_н – время начала работы – до t_ПЛ в соответствии с технологическими требованиями. Если через П(t) обозначить плотность распределения объема работ во времени, то, очевидно, можно записать следующие равенства:

.

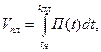
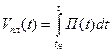По ряду объективных и субъективных причин скорость выполнения работы, т.е. П(t) отклоняется от запланированной. Поэтому в процессе осуществления данной работы с целью контроля приходится сравнивать истинный объем выполненной работы, являющийся случайной величиной, с плановым объемом, который должен был быть выполнен к моменту контроля t_i.

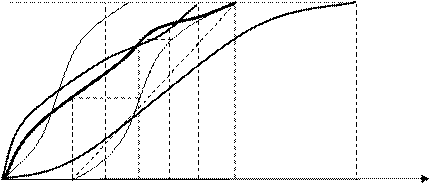
Для дальнейших рассуждений по определению шага опроса обратимся к рис. 5.1.

V

V_ПЛ

V₀(t) V_ПС(t)

V_ПЛ(t)

V(t)

t_H t₁ t₀ t₂ t_i t_i+1 t_ПЛ t_ПС t

Рис. 5.1. Интегральные кривые выполнения работ

На рис. 5.1. V_ПЛ(t) – плановая интегральная кривая выполнения работы, построенная при условии, что скорость или интенсивность выполнения работы равна П_ПЛ(t); V₀(t) – интегральная кривая выполнения работы, построенная при условии, что скорость выполнения работы будет максимально возможной П₀(t) для данной организации; наконец, V_ПС(t) – интегральная кривая выполнения работы, построенная при условии, что скорость ее выполнения П_ПС(t) будет минимальной.

Очевидно, что П_ПС(t)£ П_ПЛ(t)£ П₀(t), tÎ(0, T). Для определения частоты опроса на качественном уровне воспользуемся следующей геометрической иллюстрацией. Переместим кривую V₀(t) в направлении оси абсцисс таким образом, чтобы точка (t₀, V_ПЛ) совпала с точкой (t_ПЛ, V_ПЛ). Тогда начальная точка в функции V₀(t) переместится из точки (t_н, 0) в точку (t₁, 0). Очевидно, что если даже до момента t₁ работа вообще не выполнялась, то все еще имеется возможность, отличная от нуля, выполнить эту работу в установленный срок. Если же первый опрос будет произведен позже момента t₁, то поскольку наибольшая скорость выполнения работы определяется кривой V₀(t), то срок t_ПЛ может быть уже и не обеспечен даже в случае оптимальных условий использования наличных производительных и материальных ресурсов.

Таким образом, первый опрос о состоянии работы должен быть произведен в срок, определяемый промежутком (t_н, t₁). Приняв предельное значение t₁ и проведя опрос, мы получим сведения о выполненном объеме работ V(t₁), который равен значению V(t) в точке с абсциссой t₂. Проведя через эту точку кривой (V(t₁), t₁) линию, параллельную оси абсцисс, до пересечения со смещенной кривой V₀(t) получим точку с абсциссой t₂, определяющую по ранее приведенным соображениям предельные значения срока второго опроса. Последующие точки опроса определяются аналогично.

Отметим некоторые особенности этого метода определения шагов опроса.

1. Шаг опроса получается переменным. Чем ближе работа к завершению, тем чаще осуществляется опрос.

2. Чем лучше идет работа на объекте, чем больше превышение V(t) над V_ПЛ(t), тем реже осуществляется опрос и тем меньше будет опросов. Наоборот, чем хуже идет выполнение работы, т.е. чем ниже идет кривая V(t) относительно V_ПЛ(t), тем чаще осуществляется опрос и принятие оперативных управляющих воздействий.

3. Существует опасность, что на некотором шаге опроса (в том числе и первом) мы окажемся на смещенной кривой, т.е. будут израсходованы все резервы времени. Это будет иметь место в том случае, если от момента последнего опроса до данного опроса работа совсем не выполнялась. Однако возникновение такой ситуации маловероятно, т.к. возможность снижения скорости выполнения работы ниже некоторой, соответствующей пессимистической оценке практически невозможно в реальных ситуациях.

Поскольку возможность движения строго по кривой V_ПЛ(t) невелика, задача управляющего органа в этом случае состоит в том, чтобы обеспечить наименьшую задержку относительно срока t_ПЛ, а также изменить условия выполнения работ в случае задержки таким образом, чтобы повысить скорость выполнения, т.е. чтобы ее график прошел выше кривой V(t) за счет привлечения дополнительных ресурсов, расширения фронта работ и т.п.

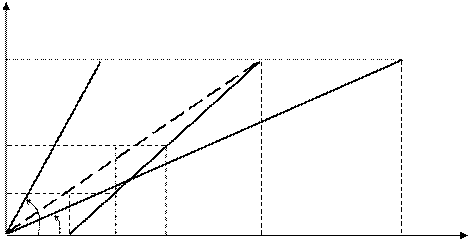
Чтобы получить аналитическое выражение для предельного момента (i+1)-го опроса t_i+1 сделаем допущение, что скорости выполнения работ П_ПС, П_ПЛ, П₀ постоянны и, значит, функции П_ПС, П_ПЛ, V₀, отражающие ход выполнения работы изобразятся в виде прямых (см. рис. 5.2).

На этом рисунке 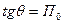, , t_ПС – пессимистический срок окончания работы.

V(t)

V_ПЛ

V₀(t) V_ПС(t)

V¹(t₁)

q

j

t_H t₁ t₂ t₃ … t_ПЛ t_ПС t

Рис. 5.2. Ход выполнения работ

Из предыдущего ясно, что первый момент опроса t₁ можно найти, если провести через точку (t_ПЛ, V_ПЛ) прямую, параллельную прямой V₀(t). Из геометрических соображений величина t₁ определяется следующим образом:

.

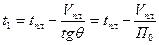Приняв t₁ за точку первого опроса, можно получить сведения о фактическом объеме выполненной работы V¹(t₁). Этот объем по смыслу должен быть отличен от нуля и, более того, можно утверждать, что точка А¹(t₁) лежит между прямыми, соответствующими ходу работ с минимальной и максимальной скоростями выполнения. Проведя через точку с координатами (V¹(t₁), t₁) прямую, параллельную оси абсцисс и соответствующую нулевой скорости выполнения работы до пересечения с прямой, параллельной прямой V₀(t), получим точку t₂, определяемую из следующих равенств:

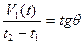, откуда .

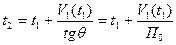Или, подставляя сюда значение для t₁ окончательно получим:

.

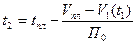Рассуждая аналогично, получим формулу для аналитического выражения момента (i+1)-го опроса на основании измерения фактически выполненного объема в момент I-го опроса:

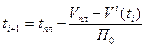. (1)

В реальных условиях П₀ не остается постоянным, т.к. после каждого опроса пересматриваются все временные оценки, в том числе и оптимистические. В этом случае последующее предельное значение момента опроса t_i+1 будет определяться точкой пересечения прямой, проходящей через точку кривой V(t_i) и параллельной оси абсцисс, с новой оптимистической кривой, вид которой определился на i-м шаге. Тогда соотношение (1) для этого случая запишется так:

,

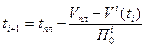где 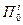- некоторое средняя оптимистическая скорость, характеризующая пересмотренные предельные возможности выполнения работы после i-го шага.

Полученные соотношения были выведены в предположении о возможности прекращения данной работы совсем, т.е. снижения скорости ее выполнения до нуля.

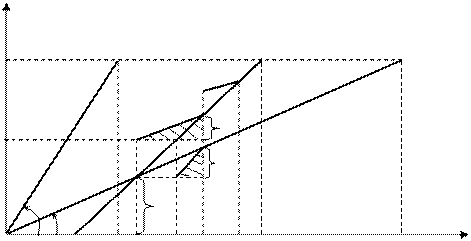
Если принять условие, что скорость выполнения работы не может быть ниже некоторой скорости, определяемой кривой V_ПС(t), то моменты опроса можно найти способом, аналогичным описанному выше, с той разницей, что вместо отрезков, параллельных оси абсцисс, используются отрезки линий, параллельных V_ПС, как это показано на рис. 4.2 для случая линейного представления функций V₀(t) и V_ПС(t). Графическое выражение для определения предельного момента (i+1)-го опроса в этом случае будет иметь вид, показанный на рис. 5.3.

V(t)

V_ПЛ

V₀(t) V_ПС(t)

x

V¹()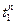

x

q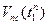

j

t_H t₁ t₀ 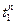t₂ 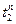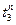t_ПЛ t_ПС t

Рис. 5.3. Графическое представление определения предельного момента

Для нахождения первого момента опроса t₁ следует провести через точку (t_ПЛ, V_ПЛ) прямую, параллельную прямой V₀(t) до пересечения с прямой V_ПС(t). Спроектировав эту точку пересечения на ось абсцисс, получим момент первого опроса 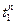. Из геометрических соображений следует:

; .

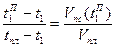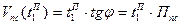Подставляя второе уравнение в первое, получим:

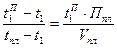, отсюда

,

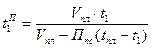или, подставляя сюда выражение для 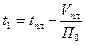, окончательно получим:

.

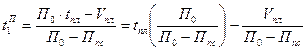Формула для аналитического выражения (i+1)-го момента на основании измерения фактически выполненного объема работы в момент i-го опроса может быть получена следующим образом. Пусть V(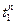) – фактически выполненный объем работы в момент времени 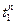. Тогда можно записать следующие равенства:

; ; .

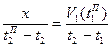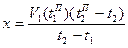Решая это уравнение относительно 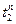, получим

.

Подставляя в это выражение выражения для:

,

,

,

,

,

.

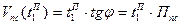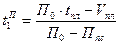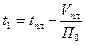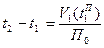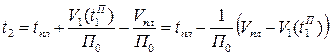Получим:

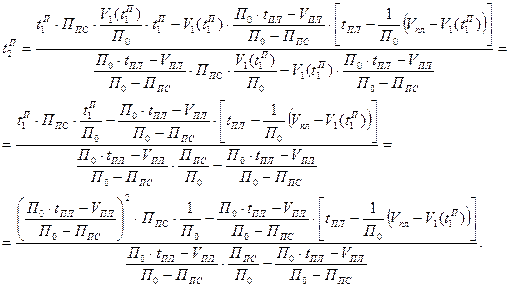
Нетрудно теперь получить выражение и для (i+1)-го момента опроса.

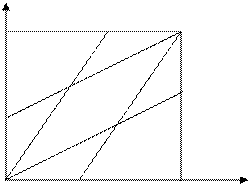
Определим ряд областей, нахождение в которых определяет характер принимаемых решений по управлению ходом выполнения работы. Для этого опять прибегнем к графической иллюстрации (см. рис. 5.4)

V

V_ПЛ G B C

H I

L

D

О Е F t

Рис. 5.4. Области принятия решений

На рисунке прямые OB и OI соответствуют функциям V₀(t) и V_ПС(t). Прямые CL и CE параллельны прямым OI и ОВ соответственно. Прямая СЕ отображает ход выполнения работ с максимальной скоростью, при котором плановое задание завершается в момент t=t_ПЛ. Прямая CL соответствует ходу выполнения с минимальной скоростью работ, завершающихся в момент t=t_ПЛ. Прямые OB, CH, OI и СЕ разбивают прямоугольник OGCF, представляющий собой совокупность всех возможных состояний системы за время 0£t£t_ПЛ, на ряд областей.

Приведем вначале классификацию этих областей, используя в качестве признака причину попадания системы в ту или иную область. По этому признаку могут быть выделены три области:

Область I – (OBCIO). В любую точку этой области можно попасть как при нормальных значениях своих параметров за счет изменений скорости выполнения работы в пределах П_ПС£ П£ П₀, так и при кратковременных положительных и отрицательных возмущениях типа болезнь исполнителей, нарушения в материально-техническом снабжении и т.п.

Область II – (OIF). В точки этой области можно попасть только в случае воздействия отрицательных возмущений, уменьшающих скорость выполнения работы до значений, меньших П_ПС.

Область III – (OGB). В точки этой области можно попасть только при воздействии положительных возмущений, увеличивающих скорость выполнения работы до значений, больших П₀.

По признаку необходимых управляющих воздействий области могут быть классифицированы следующим образом:

Область 1 (OLCE). Из любой точки этой области при нормальных условиях выполнения работы можно достигнуть точки С с координатами (t_ПЛ, V_ПЛ), т.е. выполнить плановое задание в срок при допустимом изменении скорости выполнения работы. Управляющие воздействия в этой области носят характер указания о необходимой скорости выполнения работ.

Из геометрических соображений нетрудно получить значение необходимой скорости выполнения работы в момент t:

,

где 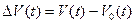. Это справедливо для случая

.

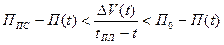При этом привлечение дополнительных ресурсов не требуется.

Область 2 (ECF). При попадании в эту область максимальная скорость выполнения работы при нормальном обеспечении ее ресурсами уже не может обеспечить возможность ее завершения в момент t_ПЛ. Для выполнения задания в плановый срок скорость должна быть увеличена до значений, больших максимальных, за счет привлечения дополнительных ресурсов. При этом скорость выполнения работы должна быть такой:

.

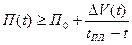Область 3 (LCG). Из этой области даже двигаясь с минимальной скоростью можно выполнить работу раньше установленного срока t_ПЛ.

Если нужно обеспечить выполнение работы в момент t_ПЛ, то путем переключения части или всех ресурсов на некоторый промежуток времени на выполнение другого задания следует уменьшить скорость до значений, меньших минимальных.

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО КУРСУ «ПРОЕКТИРОВАНИЕ АСОИУ» 2009 – 2010 учебный год

1. Классификация АСОИУ. Обобщенная схема функциональной структуры интегрированной АСОИУ

2. Структуризация АСОИУ. Виды структур АСОИУ, привести примеры.

3. Виды обеспечений АСОИУ. Назначение и структура организационного, информационного и технического обеспечений АСОИУ.

4. Виды обеспечений АСОИУ. Назначение и структура программного обеспечения АСОИУ.

5. Структура и основные компоненты комплекса программного обеспечения АСУ сложным техническим объектом.

6. Виды обеспечений АСОИУ. Назначение и структура лингвистического, математического, правового и эргономического видов обеспечений.

7. Обобщенная схема организационно-функциональной структуры АСОИУ, ее особенности и назначение.

8. Содержание проектных работ на стадиях «Формирование требований к АСОИУ», «Разработка концепции АСОИУ». Структура и состав итоговых документов этих стадий.

9. Содержание проектных работ на стадии «Техническое задание». Структура и состав итогового документа стадии.

10. Обобщенная характеристика этапа «Логическое проектирование АСОИУ».

11. Обобщенная характеристика этапа «Физическое проектирование АСОИЙ».

12. Обобщенная характеристика этапа «Программная реализация АСОИУ».

13. Методы анализа документооборота в исследуемом объекте автоматизации. Матричная информационная модель.

14. Методология описания бизнес - процессов средствами IDEF3.Привести примеры.

15. Методология функционального моделирования IDEF0. Привести примеры.

16. Структурный анализ потоков данных в АСОИУ с помощью диаграмм DFD/

17. Математическая модель анализа и оптимизации движения информационных потоков в проектируемой АСОИУ.

18. Построение макромодели АСОИУ на предпроектной стадии ее разработки.

19. Общая постановка и формализация оптимизационной задачи разбиения ИЛМ проектируемой АСОИУ на модули обработки данных.

20. Постановка и формализация задачи разбиения ИЛМ проектируемой АСОИУ на модули обработки данных с минимальным числом информационных связей между ними.

21. Постановка и формализация задачи разбиения ИЛМ проектируемой АСОИУ на модули обработки данных с минимальным временем обмена информацией между оперативной памятью управляющей ЭВМ и базой данных.

22. Обобщенная математическая модель определения рациональной структуры распределенной АСОИУ.

23. Постановка общей задачи синтеза информационного обеспечения АСОИУ модульного типа. Формализация задачи определения числа и состава информационных массивов.

24. Постановка общей задачи синтеза информационного обеспечения АСОИУ модульного типа. Формализация задачи выбора оптимальных методов организации массивов и размещения модулей и массивов во внешней памяти ЭВМ. Формализация задачи определения величины блока данных.

25. Постановка и агрегированная модель распределения ограниченных финансовых ресурсов проектной организации между затратами на НИР и ОКР.

26. Общая постановка и формализация задачи оптимального формирования тематического плана работы проектной организации.

27. Структура и требования ГОСТов к проектной документации разрабатываемой АСОИУ по общесистемным вопросам.

28. Структура и требования ГОСТов к проектной документации разрабатываемой АСОИУ по организационному обеспечению.

29. Структура и требования ГОСТов к проектной документации разрабатываемой АСОИУ по информационному обеспечению.

30. Структура и требования ГОСТов к проектной документации разрабатываемой АСОИУ по программному обеспечению.

31. Требования ГОСТов к выполнению схем алгоритмов, программ, данных и систем.

Содержание

ГЛАВА 1. АСОИУ КАК ОБЪЕКТ ПРОЕКТИРОВАНИЯ.. 2

Дата добавления: 2014-01-07