
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Простой абстрактный интерпретатор
|
|
|
|
Операционная процедура поиска ответа на вопрос была неформально описана в предыдущих разделах. Углубляясь в детали, рассмотрим абстрактный интерпретатор логических программ. Поскольку обобщенное правило modus ponens ограничено применением к основным целям, интерпретатор отвечает лишь на основные вопросы.
Абстрактный интерпретатор выполняет вычисления с ответами да/нет. Он получает программу Р и основной вопрос Q и дает ответ да, если Q выводимо из Р, и ответ нет в противном случае. Кроме того, если цель невыводима, интерпретатор может вообще не завершить работу. В этом случае не выдается никакого ответа. Рис. 1.1 демонстрирует работу интерпретатора.
Вход: Основной вопрос Q и программа P
Результат: да, если найден вывод Q из программы P,
Алгоритм: нет в противном случае.
Положить резольвенту равной Q,
пока резольвента A ,…A
,…A не пуста начало
не пуста начало
выбрать цель A , 1£ i £ n и такой основной пример предложения A ¬ B
, 1£ i £ n и такой основной пример предложения A ¬ B ,B
,B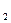 ,…B
,…B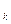 ,k³0 в P что A = A
,k³0 в P что A = A ;
;
(если такого предложения нет, то выйти из цикла); положить резольвенту равной A ,…A
,…A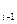 ,B
,B ,…B
,…B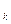 ,A
,A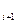 ,…,A
,…,A
конец
если резольвента пуста, то результат – да, иначе результат – нет.
Рис. 1.1. Абстрактный интерпретатор логических программ.
На любой стадии вычислений существует текущая цель, называемая резольвентой. Протоколом интерпретатора называется последовательность резольвент, которые строятся в процессе вычисления, вместе с указанием сделанного выбора. Рассмотрим вопрос сын(лот,аран)? при использовании программы 1.2, являющейся подмножеством фактов программы 1.1, которое дополнено правилами, определяющими отношения сын и дочь. На рис. 1.2 приводится протокол поиска ответа.
Протокол в неявном виде содержит вывод основного вопроса в программе. Удобнее изображать вывод в виде дерева вывода. Введем необходимые понятия.
|
|
|
Вход: сын (лот, аран)? и программа 1.2
Резольвента не пуста
Выбор: сын (лот, аран) (единственный выбор)
Выбор: сын (лот, аран) ¬ отец (аран, лот), мужчина (лот).
Новая резольвента: отец (аран, лот), мужчина (лот)?
Резольвента не пуста
Выбор: отец (аран, лот)
Выбор: отец (аран, лот).
Резольвента не пуста
Выбор: мужчина (лот)
Выбор: мужчина (лот).
Новая резольвента пуста
Результат: да
Рис.1.2. Протокол интерпретатора
отец(аврам, исаак). мужчина(исаак).
отец(аран, лот) мужчина(лот)
отец(аран, милка). женщина(милка).
отец(аран, иска). женщина(иска).
сын(Х,Y) ¬ отец(Y,Х), мужчина(Х).
дочь(Х,Y) ¬ отец(Y,Х), женщина(Х).
Программа 1.2. Отношения в библейской семье.
· Определение: Основная редукция цели G с помощью программы Р состоит в замене цели G телом того примера правила из Р, чей заголовок совпадает с данной целью. ·
Редукция является главным вычислительным шагом в логическом программировании. Она соответствует применению обобщенного правила modus ponens, а также одной итерации цикла «пока» в абстрактном интерпретаторе. Замененная при редукции цель называется снятой, появившиеся цели называются производными.
Применим данные понятия к анализу протокола на рис. 1.2. В протоколе имеются три редукции. Первая редукция снимает цель сын (лот,аран) и строит две производные цели – отец (аран.лот) и мужчина (лот). Следующая редукция применяется к цели отец(аран.лот) и не дает производных целей. Третья редукция также не дает производных целей при снятии цели мужчина (лот).
Дерево вывода состоит из вершин и ребер и изображает цели, снимаемые в процессе вычисления. Корень дерева вывода в случае простого вопроса совпадает с этим вопросом. Вершины дерева соответствуют целям, снимаемым в процессе вычисления. Направленное ребро, ведущее из одной вершины в другую, соответствует переходу от снимаемой цели к производной. Деревом вывода для конъюнктивного вопроса является просто совокупность деревьев вывода для отдельных целей в конъюнкции. Рис. 1.3 изображает дерево вывода для протокола, приведенного на рис. 1.2.
|
|
|
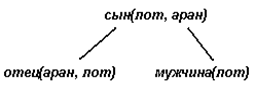
Рис. 1.3. Простое дерево вывода.
В интерпретаторе имеются два неопределенных выбора: выбор цели из резольвенты для снятия и выбор предложения (и подходящего основного примера) для редукции. Эти два выбора имеют различную природу.
Выбор цели для снятия произволен. В любой имеющейся резольвенте все цели должны быть сняты. Можно показать, что порядок снятия при построении доказательства не имеет значения. Иными словами, если существует доказательство цели, то оно является доказательством независимо от того, в каком порядке применяются редукции. В терминах дерева вывода это означает, что порядок ветвей несущественен.
Наоборот, выбор предложения и подходящего основного примера является решающим. В общем случае существует несколько вариантов предложений и бесконечно много основных примеров. Выбор производится недетерминировано. Понятие недетерминированного выбора применяется весьма плодотворно в определении многих моделей вычислений, например, в конечных автоматах и машинах Тьюринга. Недетерминированный выбор состоит в неопределенном выборе из некоторого числа альтернатив, который предположительно производится методом «предвидения»; если только некоторые из альтернатив приводят к успешному вычислению (в нашем случае – к нахождению доказательства), то одна из них и будет выбрана. Формально понятие определяется следующим образом: вычисление, содержащее недетерминированный выбор по определению заканчивается успешно, если существует последовательность недетерминированных выборов, приводящая к успеху. Конечно, ни одна из реальных машин не может непосредственно реализовать это определение.
Интерпретатор, представленный на рис. 1.1, может быть расширен так, чтобы он давал ответы и на неосновные экзистенциальные вопросы. Для этого следует ввести дополнительный шаг: угадывание основного примера вопроса. Этот шаг подобен тому, на котором интерпретатор угадывает основные примеры правил. Угадать правильный основной пример в общем случае непросто, так как это означало бы знание результата вычисления до его выполнения.
|
|
|
Чтобы избавиться от ограничений, налагаемых основными примерами, и бремени угадывания, потребуются новые понятия.
Деревья вывода позволяют использовать важную меру сложности – число вершин в дереве. Она показывает, сколько шагов редукции выполнялось при вычислении.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 430; Нарушение авторских прав?; Мы поможем в написании вашей работы!