Рекурсивные правила

До сих пор описывались правила, определяющие новые отношения в терминах существующих отношений. Важным расширением множества подобных правил являются рекурсивные определения, в которых отношения определяются в терминах этих же отношений.Один из способов перехода к рекурсивным правилам состоит в обобщении множества нерекурсивных правил.

Рассмотрим правила, описывающие прародителей, прапрародителей и т.д.:

прародитель (Предок, Потомок) ¬

родитель (Предок, Человек),

родитель (Человек, Потомок).

прапрародитель (Предок, Потомок) ¬

родитель (Предок, Человек),

прародитель (Человек, Потомок).

прапрапрародитель (Предок, Потомок) ¬

родитель (Предок, Человек),

прапрародитель (Человек, Потомок).

Можно заметить простую схему, которую мы опишем в правиле, задающем отношение предок (Предок, Потомок):

предок (Предок, Потомок) ¬

родитель (Предок, Человек), предок (Человек, Потомок).

Это правило представляет собой обобщение введенных ранее правил.

Логическая программа для отношения предок требует также и нерекурсивного правила, выбор которого влияет на значение программы. Если использовать факт предок(Х,Х), приводящий к рефлексии отношения предок, то каждый человек будет своим собственным предком. Это не соответствует интуитивному пониманию слова предок. Программа 2.5 является логической программой, определяющей отношение предок, в ней родители считаются предками.

предок (Предок, Потомок) ¬

Предок является предком субъекта Потомок.

предок (Предок, Потомок) ¬

родитель (Предок, Потомок).

предок (Предок, Потомок) ¬

родитель (Предок, Человек), предок (Человек, Потомок).

Программа 2.5. Отношение предок.

Отношение предок является транзитивным замыканием отношения родитель. В общем случае благодаря использованию рекурсивных правил в логической программе легко строится транзитивное замыкание любого отношения.

Рассмотрим программу проверки связности в ориентированном графе. Ориентированный граф может быть задан в виде логической программы с помощью набора фактов. Факт edge (Node1, Node2) входит в программу, если в графе существует ребро, ведущее из вершины Node1 в вершину Node2. На рис. 2.4 изображен некоторый граф, а программа 2.6 дает его представление в виде логической программы

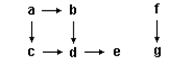
Рис. 2.4. Простой граф.

edge (a, b). edge (a, c). edge (b, d).

edge (c, d). edge (d, e). edge (f, g).

Программа 2.6. Ориентированный граф.

Две вершины графа связаны, если существует последовательность ребер, ведущая из первой вершины во вторую. Таким образом, отношение connected (Node1,Node2), являющееся истинным, если вершины Node 1 и Node 2 связаны, есть транзитивное замыкание отношения edge. Например, в графе на рис.2.4 вершины а и е связаны, а b и f – нет. Программа 2.7 описывает требуемое отношение. Значение программы совпадает с множеством целей вида connected(X,Y), где X и Y – связанные вершины. Заметим, что ввиду выбора исходного факта connected является транзитивным рефлексивным отношением

connected(Node1,Node2) ¬

вершина Node1 связна с вершиной Node2 в графе, заданном отношением edge/2.

connected (Node, Node).

соnnected (Node l, Node 2) ¬

edge (Node l, Link), connected (Link, Node 2).

Программа 2.7. Транзитивное замыкание отношения edge.

Дата добавления: 2014-01-07