Арифметика

Рекурсивное программирование

Лекция №3

В программах предыдущего раздела использовались конечные структуры данных. Сила же математики проявляется как раз на бесконечных или потенциально бесконечных структурах. Конечные примеры являются лишь частным случаем. Логические программы овладевают этой силой, используя рекурсивные типы данных.

Логические термы можно классифицировать по типам. Тип – это множество (возможно, бесконечное) термов. Некоторые типы удобно определять унарными отношениями. Отношение р/1 определяет тип р, совпадающий с множеством всех таких термов X, что выполнено р(Х).

Например, использованные ранее предикаты мужчина/1 и женщина/1 задают типы мужчина и женщина.

Более сложные типы могут быть заданы рекурсивными логическими программами. Такие типы называются рекурсивными типами. Типы, задаваемые унарными рекурсивными программами, называются простыми рекурсивными типами. Программа, задающая тип, называется определением типа.

В этой главе мы рассмотрим логические программы, задающие отношения над объектами простых рекурсивных типов, таких, как целые числа, списки и бинарные деревья.Но будут показаны программы и с более сложными типами, такими, как полиномы.

Простейший рекурсивный тип данных – натуральные числа – лежит в основании математики. Арифметика основана на натуральных числах. В данном разделе мы опишем логические программы, задающие арифметику, и хотя, как будет показано в дальнейшем, аналогичные программы на Прологе существенно отличаются от приведенных, полезность этого описания несомненна. Во-первых, обычно арифметические операции рассматриваются как функции, а не как отношения. Изучение примеров из столь знакомой области подчеркивает новый подход, необходимый при построении логических программ. Во-вторых, так будет проще обсуждать основные математические вопросы, такие, как корректность и полнота программ.

Натуральные числа строятся с помощью двух объектов – константного символа 0 и унарной функции следования s. Таким образом, все натуральные числа рекурсивно представляются в виде 0, s(0), s(s(0)), s(s(s(0))).... Используем сокращение s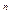(0) для обозначения натурального числа n, т. е, для обозначения n-кратного применения функции следования к 0.

Как и в предыдущей главе, каждый предикат снабжается реляционной схемой, в которой описывается подразумеваемое значение предиката.Напомним, что программа Р называется корректной относительно подразумеваемого значения М, если значение программы является подмножеством М. Программа Р полна, если М является подмножеством значения программы Р. Программа корректна и полна, если ее значение совпадает с М. Доказательство корректности устанавливает, что любое утверждение, выводимое из программы, является подразумеваемым значением программы. Доказательство полноты устанавливает, что любое подразумеваемое значение выводимо из программы. В данном разделе приводятся два типичных доказательства корректности и полноты.

Определение натуральных чисел в виде простого типа явно сформулировано в виде логической программы 3.1. Ее реляционная схема natural_number(X) предполагает, что “X есть натуральное число”. Программа состоит из одного единичного предложения и одного итерационного предложения (предложения, тело которого состоит из одной цели). Такая программа называется минимальной рекурсивной.

natural-number (X) ¬

X - натуральное число.

natural_number(0)

natural_number(s(X)) ¬ natural _number(X).

Программа 3.1. Определение натуральных чисел.

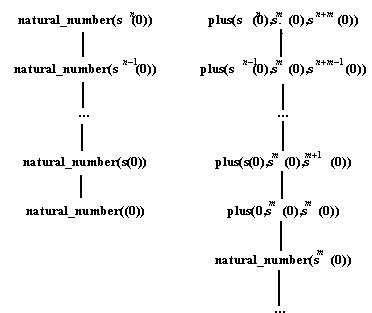
Рис. 3.1. Дерево вывода, подтверждающее полноту программ.

· Утверждение. Программа 3.1 корректна и полна относительно множества целей natural_number (s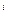(0)) при i>0.

· Доказательство. (1) Полнота. Пусть n – натуральное число. Докажем, что цель natural_number (n) выводима из программы. Для этого явно построим дерево вывода. Число n имеет вид 0 или (s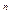(0)). Дерево вывода цели natural_number(0) тривиально. Дерево вывода цели natural_number(s(..s(0)…)) содержит n редукций, использующих правило программы 3.1 и приводящих к факту natural_number(0), как это показано на левой части рис. 3.1

(2) Корректность. Пусть цель natural_number(X) выводима из программы 3.1, количество редукций в выводе равно n. Индукцией по n докажем, что natural_number(X) принадлежит подразумеваемому значению. Если n=0, то цель должна выводится из программы с помощью единичного предложения, следовательно, X=0. Если n>0, то цель должна иметь вид natural_number(s(X1)), так как лишь такие цели выводимы с помощью правила программы, причем natural_number(X1) выводимо с использованием n– 1 редукций. По предположению индукции nalural_number(X1) принадлежит подразумеваемому значению программы, т.е. X1 = s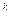(0) для некоторого k>0. ·

Существует естественный порядок натуральных чисел. Программа 3.2 является логической программой, задающей отношение “меньше или равно”, соответствующее этому порядку.

X 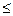Y

Х и У – натуральные числа, такие, что Х меньше или равно Y.

0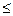X ¬ natural _number(X).

s(X)s(X) 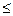s(Y)¬X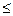Y.

natural_number(X) ¬ См. программу 3.1.

Программа 3.2. Отношение меньше или равно.

Мы записываем это отношение с помощью бинарного инфиксного символа (оператора) 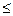в соответствии с привычной математической записью. Выражение 0 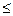Х есть не что иное, как терм с функтором 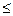/2 и аргументами 0 и X, и синтаксически эквивалентно 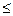(0,X).

Реляционной схемой будет 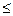N N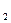. Подразумеваемое значение программы 3.2 – все основные факты вида Х 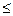Y, где Х и У – натуральные числа и число Х не больше числа Y.

Рекурсивное определение отношения 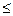не является «вычислительно эффективным». Дерево вывода, доказывающее, что конкретное п меньше конкретного w, содержит т + 2 вершины. Обычно считается, что сравнение двух чисел выполняется за один шаг независимо от величины чисел. В действительности Пролог не определяет арифметические операции на основании приведенных здесь аксиом, а непосредственно использует встроенные арифметические операции компьютера.

Сложение является базовой операцией, определяющей отношение между двумя натуральными числами и их суммой. Ранее с помощью таблицы задавалось отношение плюс для всех необходимых натуральных чисел. Рекурсивная программа позволяет задавать это отношение изящнее и компактнее, так, как это сделано в программе 3.3. Подразумеваемое значение программы – множество фактов вида plus(X,Y,Z), где X, Y и Z – натуральные числа и Х + Y = Z.

plus(X,Y,Z) ¬

X, У и Z – натуральные числа, такие, что Z есть сумма Х и Y.

plus(0,X,X) ¬ natural number(X).

plus(s(X),Y,s(Z)) ¬ plus(X,Y,Z).

natural_number(X) ¬ См. программу 3.1.

Программа 3.3. Сложение.

· Утверждение. Программы 3.1 и 3.3 задают корректную и полную аксиоматизацию сложения относительно стандартного подразумеваемого значения предиката plus/3.

· Доказательство. (1) Полнота. Пусть X, У и Z – натуральные числа, причем Z = Х + Y. Построим дерево вывода цели plus(X,Y,Z). Если Х равно 0, то У равно Z. Так как программа 3.1 полная аксиоматизация натуральных чисел, то найдется дерево вывода для цели natural_number(Y), которое легко преобразуется в дерево вывода для цели plus(0,Y,Y). Пусть теперь Х равно s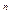(0) для некоторого п. Если Y равно s^m(0), то Z равно s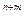(0). Дерево вывода в правой половине рис. 3,1 доказывает полноту программы.

(2) Корректность. Пусть plus(X,Y,Z) принадлежит значению программы. Методом индукции по X, как и в доказательстве предыдущего утверждения, легко установить, что Х + Y= Z. ·

Сложение обычно рассматривается как функция от двух аргументов, а не как трехместное отношение. В общем случае логическая программа, соответствующая функции от n аргументов, определяет (п + 1)-арное отношение. Вычисление значения функции происходит при постановке вопроса, в котором значения n аргументов заданы, а значение аргумента, соответствующего значению функции, не задано, решение вопроса дает значение функции при заданном значении аргументов. Чтобы прояснить аналогию, дадим функциональное определение сложения, соответствующее логической программе.

0+Х =X.

s(X)+Y = s(X+Y)

Одно из преимуществ программы, задающей отношение, перед функциональной программой состоит в том, что программу для отношения можно использовать многими способами. Например, вопрос plus(s(0),s(0),s(s(0)))? состоит в проверке равенства 1+1=2. (Конечно, десятичная запись привычнее при работе с числами.) Как и в случае отношения 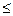, программа plus не эффективна. Дерево вывода в доказательстве того, что сумма п и т равна п + т, содержит п + т + 2 вершины.

Постановка вопроса plus(s(0),s(0),X)? (пример обычного использования программы) приводит к вычислению суммы 1 и 1. Однако столь же просто программа может быть использована и для вычитания. Для этого достаточно задать такой вопрос, как plus(s(0), X, s(s(s(0))))? Вычисленное значение Х является разностью 3 и 1, т. е. 2. Аналогично вопрос с неопределенным первым аргументом и определенными вторым и третьим аргументами также сводится к вычитанию.

Существенно новые возможности дают вопросы с многочисленными решениями. Рассмотрим вопрос plus (X, Y, s(s(s(0))))? Он означает: «Существуют ли числа Х и Y, дающие в сумме З?» Другими словами, ищутся разбиения числа 3 на два числа Х и Y. Легко видеть, что имеется несколько решений.

Вопросы с многочисленными решениями становятся интереснее, если ограничить свойства переменных в вопросе. Имеются два вида ограничений: использование дополнительных конъюнктивных членов в вопросе и уточнение переменных в вопросе. Мы рассматривали подобные примеры в случае баз данных. Упражнение (4) в конце раздела состоит, в частности, в определении предиката even (X), который истинен, если Х – четное число. Используя этот предикат, можно поставить вопрос Plus (X,Y,n),even (X), even(Y)?, который сводится к разбиению числа n на два четных числа. Второй тип ограничений иллюстрируется примером вопроса Plus(s(s(X)),s(s(Y)),п)?, в котором требуется, чтобы числа, дающие в сумме п б ыли строго больше 1.

Почти все логические программы допускают многообразное использование. Рассмотрим, например, программу 3.2, задающую отношение <. В вопросе s(0)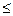s(s(0)) проверяется, верно ли, что 1 не больше 2. В вопросе Х 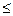s(s(0)) ищутся числа X, не большие 2. Можно даже с помощью вопроса Х 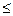У? вычислить пары чисел, одно из которых не больше другого.

Программа 3.3, определяющая сложение, не единственна. Например, логическая программа

plus(0,X,0) ¬natural_number(X).

plus(X,s(X),s(Y)) ¬ plus(X,Y,Z).

имеет в точности то же значение, что и программа 3.3. Наличие двух программ объясняется симметрией между первыми двумя аргументами. Доказательство корректности и полноты программы 3.3 преобразуется в доказательство для данной программы путем замены аргументов на симметричные.

Значение программы для отношения plus не изменится, даже если объединить эти две программы. Это объединение, однако, приводит к неудобствам, так как теперь имеется несколько деревьев вывода одной и той же цели. Как для эффективности выполнения программы, так и для выразительности программы важно, чтобы аксиоматизация логической программы была минимальной.

Мы назовем типовым условием использование предиката, определяющего тип. Типовым условием для натуральных чисел является любая цель вида natural_number(X).

Обычно программы, подобные 3.2 и 3.3, упрощаются за счет отбрасывания тела правила natural_number(X) в исходном правиле. В этом случае, однако, в значение программы попадут такие факты, как 0 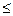а и plus (0,a,a), при произвольной константе а. Типовые условия необходимы для корректности программ. Но для упрощения программы и сокращения дерева вывода обычно они опускаются. И мы в последующих примерах программ явные типовые условия будем опускать.

Описанные основные программы используются для определения более сложных отношений. Типичный пример-определение умножения в виде повторяющегося сложения.Программа 3.4 задает требуемое отношение. Схема отношения times(X,Y,Z) означает:X, умноженное наY, равно Z.

times (X,Y,Z) ¬

X, Y и Z натуральные числа, такие, что Z равно произведению Х и Y.

times(0,X,0).

times(s(X),Y,Z) ¬ times(X,Y,W), plus(W,Y,Z).

plus(X,Y,Z) ¬ См. программу 3.3.

Программа 3.4. Умножение как повторяющееся сложение.

Возведение в степень определяется в виде повторяющегося умножения. Программа 3.5 для exp(N,X,Y) задает отношение Х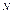 = Y. Эта программа совпадает с программой 3.4 для times (X,Y,Z), если в последней заменить times и plus соответственно на ехр и times. Исходные факты для возведения встепень – Х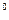= 1 для всех положительных Х и 0 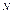= 0 для положительных значений N.

exp(N,X,Y) ¬

N, X и У -натуральные числа, такие, что У равно X, возведенному в степень N.

exp(s(X),0,0).

exp(0,s(X),s(0)).

exp(s(N),X,Y) ¬ exp(N,X,Z), times(Z,X,Y).

times(X,Y,Z) ¬ См. программу3.4

Программа 3.5. Возведение в степень как повторяющееся умножение.

Определение функции факториал использует определение умножения. Напомним, что N! = N*(N – 1)*...*2*1. Предикат factorial(N, F) сопоставляет числу N его факториал F. Аксиоматизация приведена в программе 3.6.

Не все отношения, связанные с натуральными числами, определяются рекурсивно. Отношения можно также определять в духе программ гл. 2. Примером служит программа 3.7, определяющая минимум двух чисел через отношение minimum(N1,N2,Min).

factorial(N.F) ¬

F равно факториалу числа N.

factorial(0,s(0)).

factorial(s(N),F) ¬

factorial(N,Fl)times(s(N),Fl,F),

times(X,Y,Z) ¬Cм. программу 3.4.

Программа 3.6. Вычисление факториала.

minimum (N1, N2, Min) ¬

Min равен минимуму натуральных чисел N1 и N 2.

minimum(Nl,N2,NI) ¬N1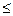N2.

minimum(Nl,N2,N2) ¬N2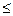Nl.

Nl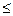N2¬См. программу 3.2.

Программа 3.7. Минимум двух чисел.

При построении программы, определяющей остаток от деления целых чисел, возникает любопытное явление различные: математические определения одного и того же понятия приводят к разным логическим программам. Программы 3.8а и 3.8б представляют собой два различных определения отношения mod(X,Y,Z), которое истинно, если Z является вычетом Х по модулю У, т. е. Z является остатком от деления Х на К Программы используют отношение <, определенное в упражнении (1) в конце раздела.

mod(X,Y,Z) ¬

Z – остаток от деления Х на Y

mod(X,Y,Z) ¬Z < Y, times(Y,Q,W), plus(W,Z,X).

Программа 3.8а. Нерекурсивное определение остатка.

mod(XYZ) ¬

Z – остаток от деления Х на Y.

mod(X,Y,X) ¬Х < Y.

mod(X,Y,Z) ¬plus(Xl,Y,X), mod (X1,Y,Z).

Программа 3.8б. Рекурсивное определение остатка.

Программа 3.8а служит примером непосредственного перевода математического определения, являющегося логическим высказыванием, в логическую программу. Программа соответствует экзистенциальному определению целого остатка: «Z равно X mod Y, если Z меньше Y и существует такое число Q, что Х = Q* Y+ Z». Математические определения в общем случае легко преобразуются в логические программы.

Можно рассмотреть связь программы 3.8а с конструктивной математикой. Несмотря на то, что определение внешне выглядит как определение существования, оно в то же время конструктивно ввиду конструктивности отношений <, р1us и times. Например, число 0, требуемое в определении, будет явно вычислено с помощью отношения times в любом конкретном вычислении отношения mod.

Программа 3.86 в отличие от программы 3.8а определена рекурсивно. Программа описывает алгоритм нахождения целого остатка, основанный на многократном вычитании. Первое правило утверждает, что Х modY равно X, если X меньше У. Второе правило утверждает, что Х mod Y совпадает с Х – Y mod Y. Процесс вычисления при определении остатка состоит в последовательном вычитании Y из X, пока не будет получена величина, меньшая У. Ясно, что это вычисление приводит к правильному значению.

Математическая функция XmodY определена при Y= 0. Ни программа 3.8a ни программа 3.8б не включают цель mod(X,0,Z) в значение программы для любых X, Z. Проверка отношения «<» гарантирует это.

Наша вычислительная модель дает возможность сравнить две программы вычисления mod. Выбрав конкретные числа X, У и Z, удовлетворяющие отношению mod, мы можем сравнить деревья вывода, В общем случае дерево вывода программы 3.8б будет меньше дерева вывода программы 3.8а. В этом смысле программа 3.86 «эффективнее».

Другим примером непосредственного перевода математического определения в логическую программу служит программа, определяющая функцию Аккермана. Функция Аккермана – простейший пример рекурсивной функции, не являющейся примитивно рекурсивной. Это функция от двух аргументов, определяемая тремя равенствами:

ackermann(0,N) = N + 1.

ackermann(M,0) = ackermann(M – 1,1).

ackermann(M,N) == ackermann(M – l,ackermann(M,N – 1)).

Программа 3.9 представляет собой запись функционального определения в виде логической программы. Предикат ackermann(M,N,A) означает, что А = ackermann(M,N). Третье правило содержит два вызова функции Аккермана, один – для вычисления второго аргумента.

ackermanfi(X,Y,A) ¬

А равно значению функции Аккермана для натуральных чисел Х и Y

ackermann(0,N,s(N)).

ackermann(s(M),0,Val) ¬ ackermann(M,s(0),Val),

ackermann(s(M),s(N),Val) ¬

ackermann(s(M),N,Val1),

ackermann(M,Vall,Val,A).

Программа 3.9. Функция Аккермана.

В функциональном определении эти два вызова выглядят очевиднее. Вообще, функциональная запись более естественна для чисто функциональных определений, как в случае функции Аккермана. Аналогичным примером является программа 3.8а. Запись выражения X=Q*Y+Z, являющегося утверждением о функциях, в виде логической программы выглядит несколько неуклюже.

Заключительным примером данного раздела является алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел, записанный в виде логической программы. Подобно программе 3.8б, это – рекурсивная программа, не использующая рекурсивное задание целых чисел. Схема отношения – gcd(X,Y,.Z), а подразумеваемое значение Z является наибольшим общим делителем (н.о.д.) двух натуральных чисел Х и У В данной программе для задания отношения mod используется любая из двух программ – 3.8а или 3.8б.

Первое правило программы 3.10 отражает логическую сущность алгоритма Евклида. Н.о.д. чисел Х и У совпадает с н.о.д. У и XmodY.

gcd(X.Y,Z) ¬

Z является наибольшим общим делителем натуральных чисел Х и Y

gcd(X,Y,Gcd) ¬mod(X,Y,Z),gcd(Y,Z,Gcd)

gcd(0,X,0) ¬X>0.

Программа 3.10. Алгоритм Евклида.

Доказательство корректности программы 3.10 зависит от корректности предыдущего математического утверждения о наибольшем общем делителе. Доказательство корректности алгоритма Евклида также основано на этом математическом утверждении

Второе предложение программы 3.10 является исходным фактом Следует указать, что Х должно быть больше 0, чтобы исключить gcd(0,0,0) из значения программы. Н.о.д. пары 0 и 0 не определен.

Дата добавления: 2014-01-07